Уроки 2 - 3
Информация и вероятность. Формула Хартли. Формула Шеннона
(§1. Количество информации)
Содержание урока
Информация и вероятность
Информация и вероятность
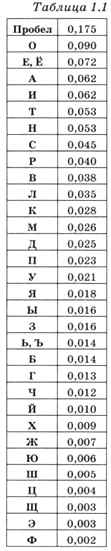
Всё, что написано в предыдущем пункте, верно только при одном уточнении: все события (символы алфавита) одинаково ожидаемы, т. е. нельзя заранее сказать, что какой-то символ встречается чаще, а какой-то — реже. В реальности это предположение не всегда верно. Например, в тексте на русском языке некоторые символы встречаются часто, а некоторые — очень редко. Числа во втором столбце табл. 1.1 означают относительную долю символа в больших текстах. Например, доля 0,175 для пробела означает, что примерно 17,5% всех символов в текстах на русском языке — пробелы.
Иногда среди всех возможных событий есть ожидаемые и неожиданные. Например, на вопрос «Идёт ли сейчас снег?» летом мы ожидаем услышать ответ «Нет». При этом ответ «Да» будет очень неожиданным, и после его получения наши дальнейшие планы могут сильно измениться. Это значит, что при таком ответе мы получаем гораздо больше информации. Как её измерить точно?
Сначала нужно разобраться с тем, что значит «менее ожидаемое» событие и «более ожидаемое». Математики в этом случае используют понятие «вероятность»: если событие более ожидаемое, то его вероятность (точнее, вероятность того, что оно произойдёт) больше.
Вероятность — это число в интервале от 0 до 1. В математике вероятность принято обозначать буквой р (от латинского probabi- lis — вероятный, возможный).
Сначала рассмотрим предельные случаи, когда вероятность равна 0 или 1. Пусть, например, х — некоторое неизвестное вещественное число, которое задумал ведущий. Вы знаете, что для любого вещественного х всегда х2 ≥ 0. В этом случае считают, что вероятность события х2 ≥ 0 равна 1 (событие х2 ≥ 0 обязательно произойдёт). Часто вероятность измеряют в процентах от 1, тогда вероятность события х2 ≥ 0 равна 100%. В то же время вероятность события х2 < 0 равна нулю, это значит, что событие х2 < 0 никогда не произойдёт.
Теперь предположим, что мы бросаем монету и смотрим, какой стороной она упала, «орлом» или «решкой». Если повторять этот опыт много раз, мы заметим, что количество «орлов» и «решек» примерно равно (конечно, если монета не имеет дефектов). При этом вероятность каждого из двух событий равна 0,5, или 50%. Скорее всего, вы слышали выражение «50 на 50», которое означает, что ни одному из двух вариантов нельзя отдать предпочтение — их вероятности равны.
Вероятность события можно определить с помощью большого количества испытаний. Если из N испытаний нужное нам событие случилось m раз, то вероятность такого события можно оценить как m/N. Например, классический игральный кубик имеет 6 граней; если кубик качественный, вероятность выпадения каждой грани равна 1/6. Вероятность выпадения чётного числа можно подсчитать так: среди чисел от 1 до 6 всего 3 чётных числа, поэтому при большом числе испытаний в половине случаев (в 3 из 6) будут выпадать чётные числа, т. е. вероятность равна 0,5. А вероятность выпадения числа, меньшего 3, равна 2/6 = = 1/3 ≈ 0,33, потому что только 2 из 6 чисел (1 и 2) удовлетворяют условию.
Теперь можно переходить к главному вопросу: как вычислить количество информации, если в сообщении получен символ, вероятность появления которого равна р. Попробуем сначала определить, какими свойствами должна обладать эта величина, исходя из «здравого смысла».

Во-первых, чем меньше вероятность, тем более неожидан символ и тем больше информации мы получили. Если вероятность события близка к нулю, количество информации должно стремиться к бесконечности (получение такого символа очень неожиданно).
Во-вторых, представим себе, что мы получаем символы только одного вида, например только буквы «А». Тогда вероятность появления символа «А» равна 1 и никакой новой информации в этом символе для нас нет — мы всё заранее знали. Следовательно, при р = 1 информация должна быть равна нулю.
В-третьих, «здравый смысл» подсказывает, что когда мы бросаем игральный кубик два (три, 102, 1002) раза, мы получаем информации в два (три, 102, 1002) раза больше, чем при однократном бросании кубика. Это свойство называют принципом аддитивности (сложения).
Математики доказали, что этими свойствами обладает только логарифмическая функция вида f(p) = -К • log2 p, где коэффициент К можно выбирать произвольно, как удобно в конкретной задаче. Если взять К = 1, мы получим количество информации в битах.
Если событие имеет вероятность р, то количество информации в битах, полученное в сообщении об этом событии, равно
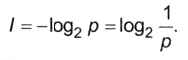
Поскольку вероятность р не больше 1, количество информации не может быть меньше нуля. Легко проверить, что если вероятность равна 1, то количество полученной информации равно нулю. Если вероятность стремится к 0, величина log2p стремится к -∞, а количество информации — к ∞.
Третье свойство (аддитивность, сложение вероятностей) проверим на примере. Пусть есть два мешка, в каждом из которых лежат 8 шариков разного цвета. Вычислим, какое количество информации мы получили из сообщения «Из первого мешка вытащили (наугад) красный шарик, а из второго — зелёный». Из каждого мешка можно вытащить один из восьми шариков, т. е. вероятность вытащить какой-то определённый шарик равна 1/8. Следовательно, количество информации в сообщении «Из первого мешка вытащили красный шарик» равно
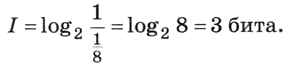
Точно такую же информацию, 3 бита, мы получаем из сообщения «Из второго мешка вытащили зелёный шарик».
Теперь посмотрим, какое количество информации несёт исходное полное сообщение «Из первого мешка вытащили (наугад) красный шарик, а из второго — зелёный». Какова вероятность именно этого исхода? Есть 8 способов вытащить шарик из каждого мешка, всего получаем 8 • 8 = 64 варианта, поэтому вероятность каждого из них равна 1/64. Тогда количество информации в сообщении равно
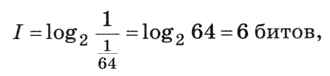
т. е. равно сумме количеств информации в двух отдельных сообщениях. Мы показали, что свойство аддитивности выполняется.
Возможно, вы уже заметили, что последний пример фактически свёлся к использованию формулы Хартли. Если все N вариантов имеют равные вероятности, то вероятность каждого варианта равна р = 1/N, следовательно, количество информации о любом из N возможных событий вычисляется как

Этот результат совпадает с формулой Хартли.
Однако формулу Хартли нельзя использовать, если вероятности событий разные. Пусть, например, детям раздают воздушные шарики разного цвета, причём 7 из каждых 10 шариков — зелёные. Какое количество информации содержится в сообщении «Маша получила зелёный шарик»? Здесь формула Хартли неприменима, однако можно использовать формулу (1). Вероятность того, что Маше достался зелёный шарик, равна 7/10, а количество информации вычисляется как
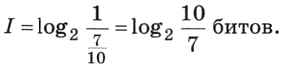
Величина под знаком двоичного логарифма не является степенью двойки. Как её вычислить? Для этого используется свойство логарифма, позволяющее переходить к другому основанию, например, к десятичным или натуральным логарифмам, которые умеют вычислять калькуляторы:
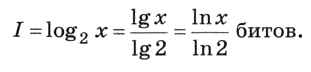
В данном случае получаем
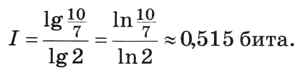
Следующая страница  Вопросы и задания
Вопросы и задания

