Урок 13
Формы представления информации.
Метод координат

Способы кодирования информации

Одна и та же информация может быть представлена разными кодами, иначе говоря, в разных формах.

Люди выработали множество форм представления информации. К ним относятся: разговорные языки (русский, английский, немецкий — всего более 2000 языков), язык мимики и жестов, язык рисунков и чертежей, научные языки (например, язык математики), языки искусства (музыка, живопись, скульптура), специальные языки (азбука Брайля, азбука Морзе, флажковая азбука).

Способ кодирования (форма представления) информации зависит от цели, ради которой осуществляется кодирование. Такими целями могут быть сокращение записи, засекречивание (шифровка) информации, удобство обработки и т. п.

Чаще всего применяют следующие способы кодирования информации:
1) графический — с помощью рисунков или значков;
2) числовой — с помощью чисел:
3) символьный с помощью символов того же алфавита, что и исходный текст.

Переход от одной формы представления информации к другой, более удобной для хранения, передачи или обработки, также называют кодированием.

Действия по восстановлению первоначальной формы представления информации принято называть декодированием. Для декодирования надо знать код.

Самое главное

Выбор способа кодирования зависит от цели, ради которой оно осуществляется.

Существует три основных способа кодирования информации: графический, числовой, символьный.

Чтобы декодировать закодированное сообщение, необходимо знать код.

Вопросы и задания

1. Какие формы представления информации вы знаете? Расскажите об одной из них.

2. Зависит ли форма представления информации от носителя информации (бумага, камень, электронный носителя информации)?

3. Выразите словами смысл следующего арифметического выражения:

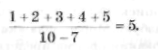
4. Мальчик заменил каждую букву своего имени её номером в алфавите. Получилось 18 21 19 13 1 15. Как зовут мальчика?

5. Зная, что каждая буква исходного текста заменяется третьей после неё буквой в алфавите русского языка, который считается записанным по кругу, декодируйте следующие сообщения:

                                                а) жуцёг льл, г ргмжиыя — дзузёл;
                                                б) фхгуюм жуцё оцъыз рсеюш жецш.

6. Каждой букве алфавита поставлена в соответствие пара чисел: первое число - номер столбца, а второе — номер строки следующей кодовой таблицы:

Пользуясь данной таблицей, расшифруйте головоломку: (1,1), (2,2), (1,3), (3,2), (10,3), (3,3), (12,1), (4,2), (5,1), (4,2), (12,2), (12,1), (1,1), (4,2), (5,1), (12,1), (1,1), (2,2), (1,3), (3,2), (10,3), (3,3), (5,1), (12,1), (1,2), (5,1), (3,2), (4,2), (5,2), (1,2), (1,3), (6,3), (4,2), (12,3).

Метод координат

«Лучше один раз увидеть, чем сто раз услышать», — гласит народная мудрость. Действительно, рисунки, схемы, чертежи и графики способны заменить нам долгие разъяснения.

Любая, в том числе и графическая, информация может быть представлена с помощью чисел. Чтобы «связать» числа и точки, используют системы координат. Простейшую из них - числовую ось вы уже рассматривали на уроках математики.

Мы с вами рассмотрим прямоугольную систему координат. Её также называют прямоугольной декартовой системой координат — в честь французского математика Рене Декарта.

Нарисуем на листе в клетку две перпендикулярные оси, точку их пересечения обозначим через О.

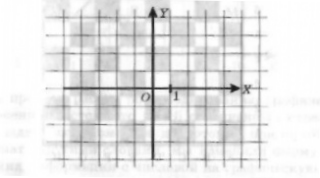
Горизонтальная ось называется осью ОХ, вертикальная — осью OY. Место пересечения осей ОХ и OY называется началом координат, которое также обозначают цифрой 0 («ноль»). Каждая точка на координатной плоскости имеет свой точный адрес.

Это пара чисел: первое число по оси ОХ, второе по оси ОУ. Эти числа называются координатами точки. А чтобы не путать порядок следования координат, вспомните, как устроены наши дома: сначала мы заходим в нужный подъезд (по оси ОХ), а затем поднимаемся на нужный этаж (по оси ОУ).

Посмотрите на шахматную доску. Вдоль её нижнего края идет ряд букв, а вдоль левого — ряд цифр. С их помощью можно однозначно определять положение любой фигуры на шахматной доске.

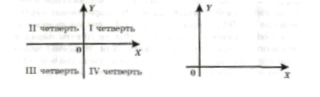
Оси координат разбивают плоскость на четыре части, которые называются координатными четвертями. Далее мы будем работать только в первой координатной четверти.

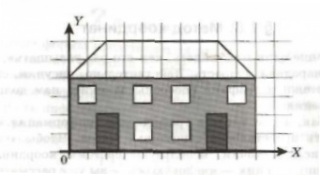
Пример. Известны координаты пятнадцати точек:

А(4, 1), В(4, 2), С(1, 2), Д(4, 5), Е(2, 5), F(4, 7), G(3, 7), H(5, 9), I(7, 7), J(6, 7), К(8, 5), L(6, 5), М(9, 2), N(6, 2), 0(6, 1).

Если отметить эти точки на координатной плоскости, а затем соединить их отрезками в последовательности А - В - С - D - Е — F -G - H - I - J - К - L - М - N — О - А, то получим следующий рисунок:

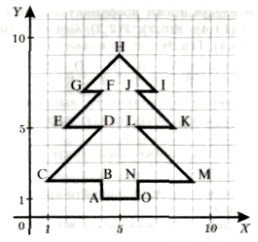
Мы провели работу по декодированию графического изображения, состоящего из 15 соединённых отрезками точек, заданных с помощью декартовых прямоугольных координат. Другими словами, мы изменили форму представления информации с числовой на графическую.

Об использовании метода координат в игре Морской бой можно прочитать в § 3.7.

Самое главное

Рисунки, схемы, чертежи, графики — графические формы представления информации. Метод координат - это один из удобных способов представления графической информации с помощью чисел.

Вопросы и задания

1. Что такое метод координат? Расскажите о нём.

2. Как метод координат применяется в географии?

3. Где вы сталкиваетесь с методом координат в быту?

4. Известны ли вам игры, основанные на методе координат? Об одной из таких игр можно прочесть в разделе    "Материалы для любознательных".

5. На координатной плоскости отметьте и пронумеруйте точки со следующими координатами:

А(2,5), В(6,5), С(11,7), D(11.4), Е(6,2), F(2,2), G(4,8), Н(9,9), I(3,2), J(3,4), К(5,4), L(5,2).

Соедините точки:

F — В — С — D — Е — F — А — G — Н — С. G - В - Е. I — J — К — L.

После проверки правильности выполнения задания можно раскрасить полученную картинку цветными карандашами.

6. Игра «Шифровальщик». Выполните действия по следующему плану:

1) на листочке в клетку нарисуйте произвольный многоугольник;
2) пронумеруйте его вершины и закодируйте их с помощью координат:
3) задайте порядок соединения вершин;
1) проверьте, не допущена ли вами ошибка при кодировании рисунка;
5) координаты точек и порядок их соединения выпишите на отдельный листок;
6) предложите кому-нибудь восстановить ваш рисунок по этому коду;
7) сравните результаты — возможно искажение информации при декодировании.