Урок 30
Разработка плана действий и его запись.
Логическая игра «Переливашки»

Разработка плана действий и его запись

Во многих информационных задачах требуется установить правило преобразования входных данных в выходные, разработать план действий, обеспечивающий нужный результат.

Рассмотрим примеры.

Задача 1

Петя и Коля играют в следующую игру: Петя задумывает правило преобразования текстовой информации. Коля может сообщать Пете любые тексты и узнавать результаты преобразования. Вопросы Коли и ответы Пети в этой игре: а —› б; мама —› нбнб; весна —› гётоб.
Отгадайте, какое правило задумал Петя.

Решение

Анализ первой пары «а —› б» позволяет предположить, что Петя каждую букву в исходном тексте заменяет на следующую по алфавиту. Проверим наше предположение на второй и третьей парах. Теперь можно сформулировать правило преобразования информации: каждая буква в исходном тексте заменяется на следующую по алфавиту.

Таким образом, мы установили возможное правило преобразования входной информации в выходную. А можно ли предложить другое правило, обеспечивающее такой же результат?

Задача 1

Два солдата подошли к реке, по которой на лодке катаются двое мальчиков. Как солдатам переправиться на другой берег, если лодка вмещает только одного солдата либо двух мальчиков, а солдата и мальчика уже не вмещает?

Решение

Введём обозначения: пусть М1 и М2 мальчики, а С1 и С2 - солдаты; стрелками (—› и ‹—) обозначим направление переправы. Запишем план переправы по пунктам:

1)    Ml и М2 —›; 
2)    Ml ‹—; 
3)    C1 —›;  
4)    М2 ‹—;

5)    М1 и М2 —›; 
6)    М1 ‹—; 
7)    С2 —›; 
8)    М2 ‹—. 

А теперь представим решение в более наглядной форме — в виде таблицы:

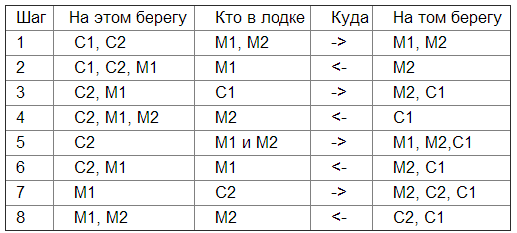
В разделе    "Материалы для любознательных" приведён ещё один пример задачи, решение которой (план действий) удобно представлять в табличной форме..

Самое главное

При решении математических или логических задач осуществляется обработка информации, ведущая к получению новой информации.

Во многих информационных задачах требуется разгадать правило преобразования входных данных в выходные, разработать план действий, обеспечивающий нужный результат.

План действий может быть записан по пунктам, представлен в виде таблицы или схемы.

Вопросы и задания

1. Можно ли утверждать, что для успешного решения математических задач достаточно знать все изученные формулы, а рассуждать логически не обязательно? Приведите пример.

2. Используете ли вы планы действий при обработке информации на уроках русского языка? Приведите примеры.

3. От чего зависит выбор формы представления плана действий?

4. Какие математические формулы должен знать человек, занимающийся ремонтом квартиры?

5. Нужны ли при решении житейских задач знания, получаемые вами в школе? Приведите примеры.

6. Решите следующие примеры самым удобным способом: 1 — с помощью таблицы умножения; 2 - подбором; 3 — разложением на удобные слагаемые. Укажите способ вычислений в квадратике, рядом с каждым примером.

7. Возле школы растут шесть деревьев: сосна, берёза, липа, тополь, ель и клён. Какое из этих деревьев самое высокое и какое самое низкое, если известно, что берёза ниже тополя, липа выше клёна, сосна ниже ели, липа ниже берёзы, сосна выше тополя?

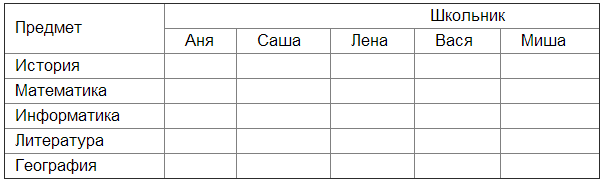
8. Пятеро одноклассников — Аня, Саша, Лена, Вася и Миша — стали победителями школьных олимпиад по истории, математике, информатике, литературе и географии. Известно, что:

1) победитель олимпиады по информатике учит Аню и Сашу работе на компьютере;
2) Лена и Вася тоже заинтересовались информатикой;
3) Саша всегда побаивался истории;
4) Лена, Саша и победитель олимпиады по литературе занимаются плаванием:
5) Саша и Лена поздравили победителя олимпиады по математике;
6) Аня сожалеет о том, что у нее остаётся мало времени на литературу.
Победителем какой олимпиады стал каждый из этих ребят?

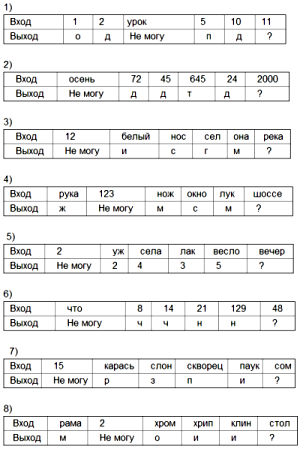
9. Некое устройство настраивается на одну из восьми программ преобразования числовой или текстовой информации. Проанализировав приведенные ниже протоколы испытаний, определите вид информации и правило её преобразования.

10. На берeгy реки стоит крестьянин с лодкой, а рядом с ним волк, коза и капуста. Крестьянин должен переправиться сам и перевезти волка, козу и капусту на другой берег. Однако в лодку кроме крестьянина помещается либо только волк, либо только коза, либо только капуста. Оставлять волка с козой либо козу с капустой без присмотра нельзя — волк может съесть козу, а коза — капусту. Как должен вести себя крестьянин?

Оформите план переправы любым известным вам способом.

Логическая игра «Переливашки»

Виртуальная лаборатория "Переливания" предназначена для решения задач, основанных на модели переливания (или пересыпания) содержимого между сосудами заданной емкости.

При решении задач возможны также "источник" жидкости и "сток" - т.е. сосуды неограниченной емкости, из которых можно наполнять "рабочие" емкости или выливать из них содержимое.

Для работы с лабораторией скачайте файл, запустите его и распакуйте архив.

Файл запуска лаборатории - Start-Lab-Vessels.exe, задачи загружаются из папки «Материалы к урокам»

Источником
виртуальной лаборатории "Переливания"
является сайт ФГАУ ГНИИ ИТТ "Информика" (Единая коллекция ЦОР)