Материал
для любознательных
Ханойская башня, или Один замечательный алгоритм
Одна из древних легенд гласит: «В непроходимых джунглях недалеко от города Ханоя есть храм бога Брамы. В нем находится бронзовая плита с тремя алмазными стержнями. На один из стержней бог при сотворении мира нанизал 64 диска разных диаметров из чистого золота. Наибольший диск лежит на бронзовой плите, а остальные образуют пирамиду, сужающуюся кверху. Это башня Брамы. Работая день и ночь, жрецы храма переносят диски с одного стержня на другой, следуя законам Брамы:
1) диски можно перемещать с одного стержня на другой только по одному;
2) нельзя класть больший диск на меньший;
3) нельзя откладывать диски в сторону, при переносе дисков с одного стержня на другой можно использовать промежуточный третий стержень, на котором диски должны находиться тоже только в виде пирамиды, сужающейся кверху.
Когда все 64 диска будут перенесены с одного стержня на другой, наступит конец света».
Эта древняя легенда положена в основу задачи о Ханойской башне: переместить n дисков со стержня 1 на стержень 3, используя промежуточный стержень 2 и соблюдая законы Брамы.

Если башня состоит из одного диска, то она переносится за один ход: 1 → 3.
Башня из двух дисков переносится за три хода: 1 → 2, 1 → 3, 2 → 3.
Для переноса башни из трех дисков потребуется уже семь ходов: 1 → 3, 1 → 2, 3 → 2, 1 → 3, 2 → 1, 2 → 3, 1 → 3. Обратите внимание, за первые три хода мы переносим башню из двух верхних дисков на второй промежуточный стержень. Затем переносим самый большой диск с первого стержня на третий и еще раз проделываем хорошо знакомую нам операцию: переносим башню из двух дисков на третий диск.
Следовательно, чтобы перенести башню из четырех дисков с первого стержня на третий, необходимо действовать по плану:
1) перенести башню из трех верхних дисков с первого стержня на второй (7 ходов);
2) самый большой диск перенести с первого стержня на третий (1 ход);
3) перенести башню из трех дисков со второго стержня на третий (7 ходов).
Всего на перенос потребуется 15 ходов. Рассуждая аналогичным образом, сосчитаем число ходов, необходимых для переноса башни из пяти дисков: 15 + 1 + 15 = 2 • 15 + 1 = 31.
Для башни из 6 дисков получаем: 2 • 31 + 1 = 63 и т. д. Рассмотренный нами алгоритм решения задачи «Ханойская башня» обладает одним удивительным свойством: в ходе его выполнения для башни, состоящей из n колец, мы используем алгоритм для чуть более простой ситуации — переноса башни, состоящей из n - 1 кольца. В свою очередь, в алгоритме для башни из n - 1 кольца используется этот же алгоритм для n - 2 колец и т. д.
Прием, когда некоторый процесс описывается через самого себя, называется рекурсией. Алгоритм решения задачи «Ханойская башня» — пример рекурсивного алгоритма.
Вопросы и задания
1. Проведите необходимые вычисления и заполните следующую таблицу:
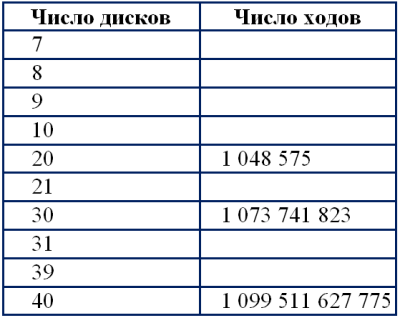
2. Назовите числа: 1 048 575,1 073 741 823, 1 099 511 627 775. Что это за числа?
3. Для того чтобы переместить башню из 64 дисков, при безошибочной работе потребуется 18 446 744 073 709 551 615 перекладываний. Сколько уйдет на это времени, если считать, что на одно перекладывание уходит одна секунда? Для выполнения вычислений используйте приложение Калькулятор.
4. Переместите башню из пяти дисков, действуя по следующим правилам: на первом, третьем и других не¬четных шагах переносите самый маленький диск «по кругу» (1-2, 2-3, 3-1); на четных шагах переносите диск между теми стержнями, где нет самого маленького кольца. Что вы можете сказать об этом алгоритме?
