Урок 5
Перевод двоичных чисел в десятичную систему счисления
Работа с приложением Калькулятор
 |
 |
 |
 |
Перевод целых десятичных чисел в двоичный код
Способ 1
Попробуем представить число 1409 в виде суммы членов второго ряда.
Воспользуемся методом разностей. Возьмем ближайший к исходному числу, но не превосходящий его член второго ряда и составим разность:
1409 - 1024 = 385.
Возьмем ближайший к полученной разности, но не превосходящий ее член второго ряда и составим разность:
385 - 256 = 129.
Аналогично составим разность: 129 - 128 = 1.
В итоге получим:
1409 = 1024 + 256 + 128 + 1 = 1 • 1024 + 0 • 512 + 1 • 256 + + 1 • 128 + 0 • 64 + 0 • 32 + 0 • 16 + 0 • 8 + 0 • 4 + 0 • 2 + 1 • 1.
Мы видим, что каждый член второго ряда может либо не входить в сумму, либо входить в нее только один раз.
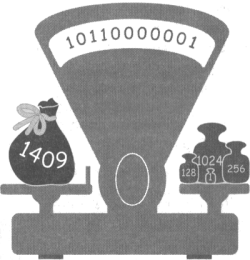
Числа 1 и 0, на которые умножаются члены второго ряда, также составляют исходное число 1409, но в его другой, двоичной записи: 10110000001.
Результат записывают так:
140910 = 101100000012.
Исходное число мы записали с помощью 0 и 1, другими словами, получили двоичный код этого числа, или представили число в двоичной системе счисления.
Способ 2
Этот способ получения двоичного кода десятичного числа основан на записи остатков от деления исходного числа и получаемых частных на 2, продолжаемого до тех пор, пока очередное частное не окажется равным 0.
Пример:
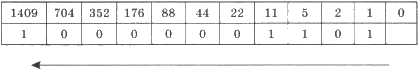
В первую ячейку верхней строки записано исходное число, а в каждую следующую — результат целочисленного деления предыдущего числа на 2.
В ячейках нижней строки записаны остатки от деления стоящих в верхней строке чисел на 2.
Последняя ячейка нижней строки остается пустой. Двоичный код исходного десятичного числа получается при последовательной записи всех остатков, начиная с последнего: 140910 = 101100000012.
Первые 20 членов натурального ряда в двоичной системе счисления записываются так: 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011,1100, 1101,1110,1111, 10000. 10001. 10010. 10011. 10100.
Перевод целых чисел из двоичной системы счисления в десятичную
Способ 1
Пусть имеется число 1111012. Его можно представить так:
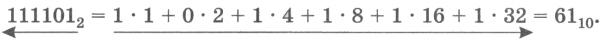
Способ 2
Возьмем то же число 1111012. Переведем единицу 6-го разряда (первая слева в записи числа) в единицы 5-го разряда, для чего 1 умножим на 2, ибо единица 6-го разряда в двоичной системе содержит 2 единицы 5-го разряда.
К полученным 2 единицам 5-го разряда прибавим имеющуюся единицу 5-го разряда. Переведем эти 3 единицы 5-го разряда в 4-й разряд и прибавим имеющуюся единицу 4-го разряда: 3 • 2 + 1 = 7.
Переведем 7 единиц 4-го разряда в 3-й разряд и прибавим имеющуюся единицу 3-го разряда: 7 • 2 + 1 = 15.
Переведем 15 единиц 3-го разряда во 2-й разряд: 15 • 2 = 30. В исходном числе во 2-м разряде единиц нет.
Переведем 30 единиц 2-го разряда в 1-й разряд и прибавим имеющуюся там единицу: 30 • 2 + 1 = 61. Мы получили, что исходное число содержит 61 единицу 1-го разряда.
Письменные вычисления удобно располагать так:
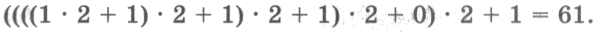
Переводить целые числа из десятичной системы счисления в двоичную систему счисления и обратно можно с помощью приложения Калькулятор.
Проведем небольшой эксперимент.
1. Запустите приложение Калькулятор и выполните команду [Вид-Инженерный]. Обратите внимание на группу переключателей, определяющих систему счисления:

2. Убедитесь, что Калькулятор настроен на работу в десятичной системе счисления. С помощью клавиатуры или мыши введите в поле ввода произвольное двузначное число. Активизируйте переключатель Bin и проследите за изменениями в окне ввода. Вернитесь в десятичную систему счисления. Очистите поле ввода.
3. Повторите пункт 2 несколько раз для других десятичных чисел.
4. Настройте Калькулятор на работу в двоичной системе счисления. Обратите внимание на то, какие кнопки Калькулятора и цифровые клавиши клавиатуры вам доступны. Поочередно введите двоичные коды 5-го, 10-го и 15-го членов натурального ряда и с помощью переключателя Dec переведите их в десятичную систему счисления.
Прочитав «Материал для любознательных», вы можете узнать много интересных сведений из истории счета и систем счисления.
Компьютерный практикум
Ресурсы ЕК ЦОР
Преобразование десятичного числа в другую систему счисления
 |
Перевод чисел из десятичной системы в двоичную
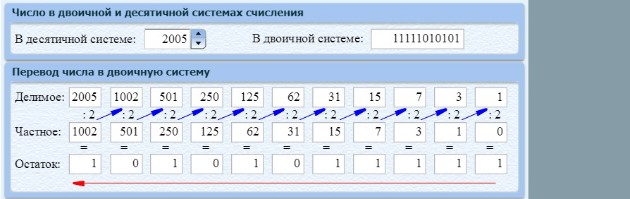 |
Перевод чисел из двоичной системы в десятичную
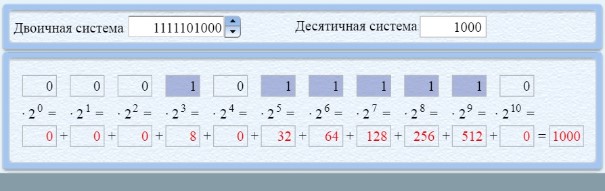 |


