Урок 25
Информационные модели на графах

Практическая работа
№10 «Схемы, графы и деревья» (задания 3 - 5)

Информационные модели на графах

Наглядным средством представления состава и структуры системы является граф. Граф состоит из вершин, связанных линиями. Если линия направленная (со стрелкой), то она называется дугой; линия ненаправленная (без стрелки) называется ребром. Линия, выходящая из некоторой вершины и входящая в нее же, называется петлей. Вершины могут изображаться кругами, овалами, точками, прямоугольниками и т. д.

Если объекты некоторой системы изобразить вершинами, а связи между ними — линиями, то мы получим информационную модель рассматриваемой системы в форме графа.

Сети

Ранее мы рассматривали графы — схемы отношений, отражающие имеющиеся связи между объектами.

Например, граф, отражающий отношение «переписываются» между объектами класса «дети», может выглядеть, как показано на рисунке ниже:

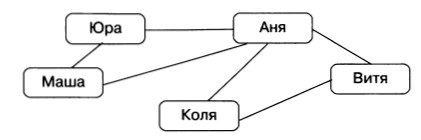
Отношение «переписываются» ( «пишут письма друг другу») является двухсторонним (симметричным). Поэтому соответствующие вершины соединены линиями без стрелок (ребрами). Граф называется неориентированным, если его вершины соединены ребрами.

Путь по вершинам и ребрам графа, включающий любое ребро графа не более одного раза, называется цепью.
Пример цепи: Юра- Аня- Витя- Коля.

Цепь, начальная и конечная вершины которой совпадают, называется циклом.
Пример цикла: Аня- Коля- Витя — Аня.

Иначе выглядит граф, отражающий отношение «пишет письма» между теми же объектами класса «дети». Линии со стрелками (дуги) придают ему совершенно иной смысл:

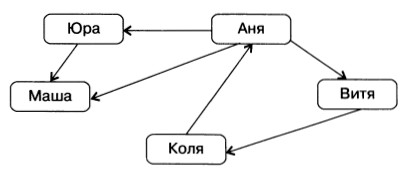
Граф называется ориентированным, если его вершины соединены дугами.

Граф называется взвешенным, если его вершины или ребра (дуги) характеризуются некоторой дополнительной информацией — весом вершины или ребра (дуги).

На рисунке ниже информация о городах Золотого кольца представлена взвешенным графом: веса его вершин — года основания городов, веса ребер — расстояния в километрах между городами.

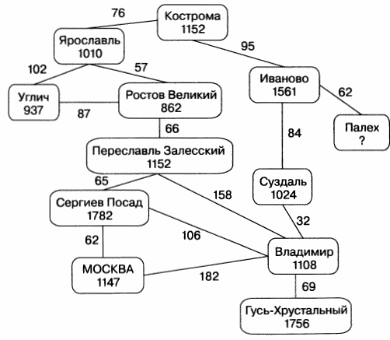
Граф с циклом называется сетью.

На следующем рисунке в виде графа представлена информационная модель сказки про Царевну-лягушку.

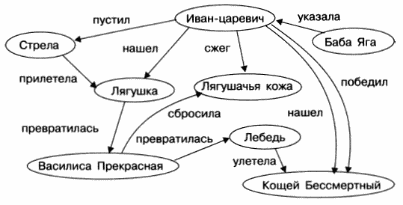
Вершины этого графа — персонажи и предметы из сказки, дуги — связи между ними. В отличие от предыдущих примеров, здесь все связи различны. Поэтому они подписываются рядом с соответствующими дугами.

Такой граф называется семантической сетью. Считается, что любую информацию можно представить в виде семантической сети, на которой будут отражены объекты (понятия) и связи (отношения) между ними.

Использование графов при решении задач

Графы удобно использовать при решении некоторых классов задач.

Задача 1

Сколькими способами можно рассадить в ряд на три стула трех учеников? Выписать все возможные случаи.

Решение этой задачи удобнее всего представить в виде дерева. За его корневую вершину возьмем произвольную точку плоскости О.

На первый стул можно посадить любого из трех учеников — обозначим их А, В и С. На схеме это соответствует трем ветвям, исходящим из точки О:

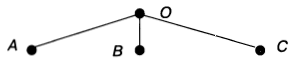
Посадив на первый стул ученика А, на второй стул можно посадить ученика В или С. Если же на первый стул сядет ученик В, то на второй можно посадить А или С. А если на первый стул сядет С, то на второй можно будет посадить А или В. Это соответствует на схеме двум ветвям, исходящим из каждой вершины первого уровня:

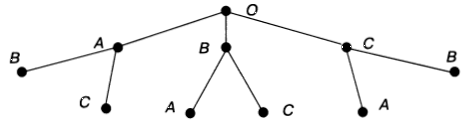
Очевидно, что третий стул в каждом случае займет оставшийся ученик. Это соответствует одной ветви дерева, которая «вырастает» на из предыдущих ветвей.

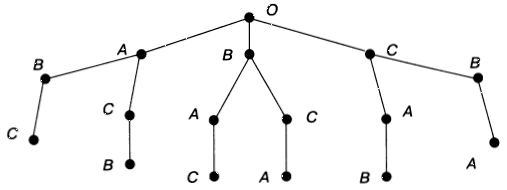
Выпишем все пути от вершин первого уровня к вершинам третьего уровня: А-В-С, А-С-В, В-А-С, В-С-А, С-А-В, С-В-А. Каждый из выписанных путей определяет один из вариантов рассаживания учеников на стулья. Так как других путей нет, то искомое число способов — 6.

Дерево можно не строить, если не требуется выписывать все возможные варианты, а нужно просто указать их число. В этом случае рассуждать нужно так: на первый стул можно усадить одного из трех человек, на второй — одного из двух оставшихся, на третий — одного оставшегося: 3 * 2 * 1 = 6.

Задача 2

Чтобы принести Царю-батюшке молодильные яблоки, должен Иван-царевич найти единственный верный путь к волшебному саду. Встретил Иван-царевич на развилке трех дорог старого ворона и вот какие советы от него услышал:

1. иди сейчас по правой тропинке;

2. на следующей развилке не выбирай правую тропинку;

3. на третьей развилке не ходи по левой тропинке.

Пролетавший мимо голубь шепнул Ивану-царевичу, что только один совет ворона верный и что обязательно надо пройти по тропинкам разных направлений. Наш герой выполнил задание и попал в волшебный сад. Каким маршрутом он воспользовался?

Обозначим левую, среднюю и правую тропинки соответственно Л, С и П. Возможные маршруты представим в виде графа. При этом подсказки ворона отметим более «жирными» ребрами. Так как только один совет ворона верен, то на графе ему будет соответствовать маршрут, имеющий одно «жирное» ребро. Этот маршрут обозначен дополнительной пунктирной линией:

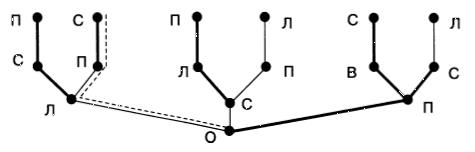
Коротко о главном

Наглядным средством представления состава и структуры системы является граф. Граф состоит из вершин, связанных линиями. Направленная линия называется дугой, ненаправленная — ребром. Линия, выходящая из некоторой вершины и входящая в нее же, называется петлей. Граф называется взвешенным, если его вершины или ребра (дуги) характеризуются некоторой дополнительной информацией — весом вершины или ребра (дуги).

Путь по вершинам и ребрам графа, включающий любое ребро графа не более одного раза, называется цепью. Цепь, начальная и конечная вершины которой совпадают, называется циклом. Разновидность графа, содержащая циклы, называется сетью.

Иерархия — это расположение частей или элементов целого в порядке от высшего к низшему. Системы, элементы которых находятся в отношениях «является разновидностью», «входит в состав» и других отношениях подчиненности, называются иерархическими системами (системами с иерархической структурой).

Граф иерархической системы называется деревом. Отличительной особенностью дерева является то, что между любыми двумя его вершинами существует единственный путь. Деревья не содержат циклов и петель.

Вопросы и задания

1. Определите сказку, для которой следующий граф определяет отношения между персонажами.

(Курочка Ряба)

2. С разных сторон на холм поднимаются три тропинки и сходятся на вершине. Перечислите множество маршрутов, по которым можно подняться на холм и спуститься с него. Решите ту же задачу, если вверх и вниз надо идти по разным тропинкам.

(Решение:
а) Вверх можно подняться по 3-м тропинкам (3 варианта), спуститься также по 3-м (3 варианта). В итоге имеем: 3 • 3 = 9 вариантов.
б) Вверх можно подняться по 3-м тропинкам (3 варианта), спуститься только по оставшимся 2-м (2 варианта). В итоге имеем: 3 • 2 = 6 вариантов)

3. Сколько трехзначных чисел можно записать с помощью цифр 1, 3, 5 и 7 при условии, что в записи числа не должно быть одинаковых цифр?

(Решение:
Число размещений 4-х элементов по 3: A = 4 • (4-1) • (4-2) • (4-3) = 4 • 3 • 3 • 1 = 24
Ответ: 24 чисел)

4. Для составления цепочек используются бусины, помеченные буквами: А, В, С, D, Е. На первом месте в цепочке стоит одна из бусин А, С, Е. На втором — любая гласная, если первая буква согласная, и любая согласная, если первая гласная.

На третьем месте – одна из бусин С, D, Е, не стоящая в цепочке на первом месте. Сколько цепочек можно создать по этому правилу?

(Решение:
а) Первая бусинка А, тогда на втором месте может быть 3 варианта бусинок и на третьем месте тоже 3 варианта. Получаем 3 • 3 = 9 вариантов;
б) Первая бусинка С, тогда на втором месте возможны 2 варианта (2 гласные) и на третьем тоже 2 варианта (Д, Е). Получаем 2 • 2 = 4 варианта;
в) Первая бусинка Е, тогда на втором месте возможны 3 варианта (3 согласные), а на третьем место — 2 варианта (С, Д) Получаем 3 • 2 = 6 вариантов;
В итоге получаем: 9 + 4 + 6 = 19 вариантов
Ответ: 19 вариантов)

5. В центре дальнего леса находилась большая поляна — самое удивительное место в Стране малышей. На ней были три колодца: один — с газировкой, второй — с молоком, третий — с морсом. Когда-то три друга Фантик, Грибок и Дружок — построили на поляне домики и целое лето жили в лесу. Другим малышам нравилось приходить к ним в гости, попить молока, газировки или морса, погулять по лесным тропинкам. Но однажды бывшие друзья поссорились, и каждый из них решил проложить собственные дорожки к колодцам так, чтобы они не пересекались с дорожками соседей.

Подумайте, почему Знайка, к которому коротышки обратились за помощью, предложил им помириться.

(Задача не имеет решения. Нельзя провести тропинки так, чтобы они не пересекались).

---

Практическая работа №10
«Схемы, графы и деревья» (задания 3 - 5)

Задание 3. Семантическая сеть. Поездка в автобусе

1. Откройте файл Поездка.doc из папки Заготовки.

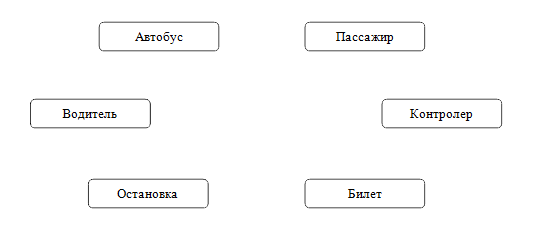
2. Дорисуйте схему отношений при поездке в автобусе. На линиях, обозначающих отношения, подпишите их названия (с помощью глаголов).

3. Сохраните результат работы в собственной папке в файле с именем Поездка 1.

Задание 4. Круговорот воды в природе

Будем считать, что круговорот воды в природе обеспечивается взаимодействием следующих объектов: водоемов (океаны, моря, озера, водохранилища, пруды и пр.), рек, подземных вод, атмосферы, облаков, почвы, растений.

Представьте круговорот воды в природе в виде графа (семантической сети), в которой вершинами являются перечисленные объекты, а дугами — отношения между ними, обеспечивающие движение воды.

Сохраните результат работы в собственной папке в файле с именем Круговорот.

Задание 5. Арифметические выражения

С помощью графа можно задать последовательность вычисления арифметического выражения. Такой граф представляет собой дерево, листьями которого являются числа, а прочими вершинами — операции. Дуги связывают вершину-операцию с вершинами-операндами. Например, для арифметического выражения 5 х (3 + 7) х (8 - 2) дерево будет иметь такой вид:

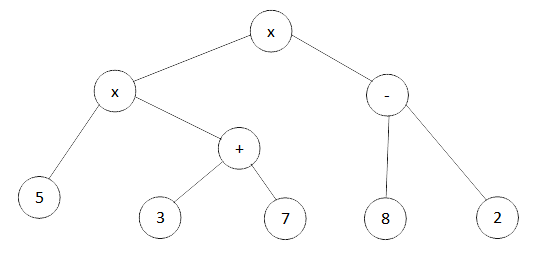
Постройте дерево для арифметического выражения: 6 x 4 + 7 x (9 - 1).

Сохраните результат работы в собственной папке в файле с именем Выражение.