Урок 26
§34. Вспомогательные алгоритмы
Содержание урока
Что такое вспомогательный алгоритм?
Два метода составления программ
Практическая работа № 23 «Вспомогательные алгоритмы»
Два метода составления программ
Мы только что использовали приём, который называется проектированием «сверху вниз» или методом последовательного уточнения. Задача разбивается на части (подзадачи), и сначала записывается основной алгоритм. Он использует вызовы ещё не написанных вспомогательных алгоритмов, каждый из которых решает свою подзадачу. Затем пишем вспомогательные алгоритмы, если нужно, так же разбивая их на части.
Есть и другой метод, который называется проектированием «снизу вверх»: сначала пишем все вспомогательные алгоритмы, а потом собираем из них, как из кубиков, основной алгоритм. Мы решим этим методом ещё одну задачу для Робота (рис. 6.17).
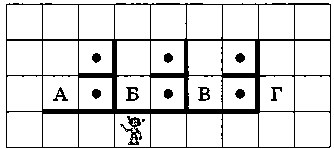
Рис. 6.17
Имеет ли смысл использовать здесь процедуру? Обоснуйте ответ.
На рисунке 6.17 мы видим три одинаковые группы из двух соседних клеток, разделённых стенкой. Поэтому можно оформить обработку такой пары клеток в виде процедуры. Выделим отдельную подзадачу, в которой Робот должен закрасить две клетки и прийти в клетку Б (рис. 6.18).
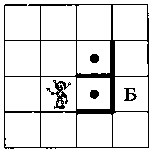
Рис. 6.18
Оформим решение подзадачи как вспомогательный алгоритм:
алг Пара
нач
вправо; закрасить
влево; вверх; вправо; закрасить
вверх; вправо; вниз; вниз
кон
Теперь вернёмся к полной задаче на рис. 6.17. Видим, что сразу применить процедуру Пара нельзя, Робота нужно сначала привести в клетку А. Затем можно вызывать процедуру, причём после того, как она закончит работу, Робот остановится в клетке Б, так что можно снова вызывать нашу процедуру. Основная программа будет выглядеть так:
использовать Робот
алг ТриПары
нач
влево; влево; вверх; вправо
Пара; Пара; Пара
кон
Конечно, после неё нужно записать расшифровку процедуры.
Применяя проектирование «снизу вверх», мы строим решение основной задачи на основе уже готовых решений более мелких задач. Так же, например, в математике доказательство новой теоремы использует уже известные результаты.
Следующая страница  Выводы. Интеллект-карта
Выводы. Интеллект-карта

