Урок 6
§9. Восьмеричная система счисления

Содержание урока

Восьмеричная система счисления

Связь с двоичной системой счисления

Алгоритм перевода восьмеричного числа в двоичную систему счисления

Алгоритм перевода двоичного числа в восьмеричную систему счисления

Арифметические действия

Применение восьмеричной системы

Выводы. Интеллект-карта

Вопросы и задания

Связь с двоичной системой счисления

Более интересен перевод из восьмеричной системы в двоичную и обратно. Конечно, можно перевести число сначала в десятичную систему, а потом — в двоичную, но для больших чисел этот способ требует достаточно сложных вычислений и может приводить к ошибкам.

Переведите число 15₈ в десятичную систему счисления, а потом — из десятичной в двоичную.

Оказывается, можно сделать перевод из восьмеричной системы в двоичную напрямую, используя тесную связь между этими системами: их основания связаны равенством 2³ = 8. Покажем это на примере восьмеричного числа 753₈. Запишем его в развёрнутой форме:

753₈ = 7 • 8² + 5 • 8¹ + 3-8^° = 7 - 2⁶ + 5 - 2³ + 3 - 2^°.

Теперь переведём отдельно каждую цифру в двоичную систему и также запишем в развёрнутой форме:

7 = 111₂ = 1 • 2² + 1 • 2¹ + 1-2^°, 5 = 101₂ = 1-2² + 1-2^°, 3 = 11₂ = 1 • 2¹ + 1^°.

Подставим эти выражения в предыдущее равенство:

753₈ = (1 • 2² + 1 • 2¹ + 1 • 2^°) • 2⁶ + (1 • 2² + 1 • 2^°) • 2³ + (1 • 2¹ + 1 • 2^°) • 2^°.

Раскрывая скобки, мы получим разложение исходного числа по степеням двойки, т. е. его развёрнутую запись в двоичной системе счисления (здесь для отсутствующих степеней числа 2 добавлены нулевые слагаемые):

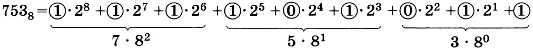
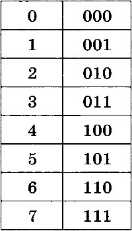
Таким образом, 753₈= 111 101 011₂. Двоичная запись разбита на триады (группы из трех цифр), каждая триада — это двоичная запись одной цифры исходного восьмеричного числа. Фактически мы каждую восьмеричную цифру отдельно переводим в двоичную систему (табл. 2.2).

Таблица 2.2

Следующая страница Алгоритм перевода восьмеричного числа в двоичную систему счисления

Cкачать материалы урока