Урок 6
§ 4. Язык — средство кодирования

Содержание урока

Язык и алфавит

Естественные и формальные языки

Сообщения и их количество

Генетический код

Выводы. Интеллект-карта

Вопросы и задания

Сообщения и их количество

С точки зрения теории информации, сообщение — это любой набор знаков некоторого алфавита. Пусть мы хотим отправлять различные сообщения одинаковой длины, используя какой-то алфавит. Конечно, чем короче будет длина сообщений, тем быстрее можно будет их передать. Но вместе с тем если сообщения будут слишком короткими, то количество различных сообщений может оказаться недостаточным. Например, из двух двоичных цифр можно составить только четыре разных сообщения: 00, 01, 10 и 11 — больше, как ни комбинируй, не получится.

Рассмотрим алфавит из четырёх знаков: @#$%. Постройте все возможные сообщения из одного знака. Постройте все возможные сообщения из двух знаков, которые начинаются с буквы @ (вторая буква может быть любой).

Для алфавита @#$% в сообщении из двух знаков первый знак можно выбрать четырьмя способами, и для каждого из них есть 4 варианта выбора второго знака. Поэтому сообщений, состоящих из двух знаков, будет 42 = 16 (рис. 2.2).

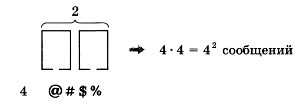
Рис. 2.2

Для алфавита из четырёх знаков определите:

а) количество сообщений из двух знаков;
б) количество сообщений из трёх знаков;
в) количество сообщений из четырёх знаков;
г) количество сообщений из L знаков.

Для алфавита из М знаков определите:

а) количество сообщений из двух знаков;
б) количество сообщений из трёх знаков;
в) количество сообщений из четырёх знаков;
г) количество сообщений из L знаков.

Если алфавит языка состоит из М знаков (имеет мощность М), количество различных сообщений длиной L знаков вычисляется как

N = M^L.

Для двоичного алфавита (его мощность равна М = 2), получается:

N = 2^L.

Алфавит языка содержит буквы «А» и «У». Определите, сколько сообщений из трёх знаков можно записать с помощью этого языка.

Алфавит языка содержит буквы «А», «О» и «У». Определите, сколько сообщений длиной не больше четырёх знаков можно записать с помощью этого языка.

Если длина сообщений может меняться (может быть равна L₁, L₂, .... L_K), то для вычисления общего количества различных сообщений нужно сложить количества сообщений для каждой возможной длины:

N = N₁ + N₂ + ... + N_K.

Следующая страница Генетический код

Cкачать материалы урока