Урок 12
Табличные модели
Содержание урока
Табличные модели. Таблицы типа «объект—свойство»
Табличные модели. Таблицы типа «объект—объект»
Табличные модели. Вопросы и задания
Системы, модели, графы. Понятие системы
Системы, модели, графы. Виды графов
Системы, модели, графы. Вопросы и задания
Дополнительный материал. Основы системологии
Системы, модели, графы
Понятие системы
Основные темы:
- понятие системы;
- граф системы;
- структура системы;
- виды графов;
- иерархические системы и деревья;
- сети.
Понятие системы
Мы будем употреблять термин система для обозначения сложных объектов.
Система — это объект, состоящий из взаимосвязанных элементов и существующий как единое целое.
Наверняка вам приходилось слышать такие словосочетания, как «система образования», «транспортная система», «система водоснабжения», «горная система». Действительно, слово «система» очень часто употребляется в речи. Под этим словом мы обычно понимаем что-то сложное, состоящее из множества элементов. Например, система городского транспорта включает в себя трамваи, автобусы, троллейбусы, трамвайные пути, линии электропередач, депо, службы технического обслуживания и пр.
Информационная модель всякой системы должна отражать ее состав и связи между составляющими ее элементами.
Граф системы
Посмотрите на рис. 2.9.
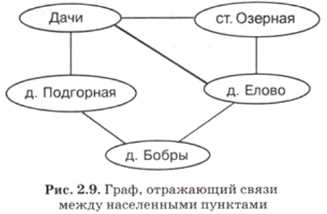
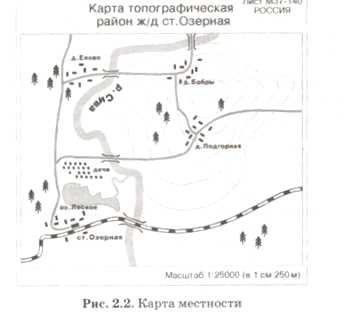
На нем в овалах записаны названия населенных пунктов с карты (см. рис. 2.2).
Пункты, связанные на карте дорогами, соединены на рисунке линиями. Однако на карту этот рисунок не похож: относительное расположение поселков, форма и длина дорог здесь не отражены. Из рисунка можно лишь узнать, между какими населенными пунктами есть дороги. Такой рисунок является графом.
Структура системы
В нашем примере мы рассматриваем данную местность как систему взаимосвязанных населенных пунктов. Элементами этой системы являются поселки. Расположение дорог между поселками определяет структуру данной системы.
Структура — это определенный порядок объединения элементов, составляющих систему.
Элементы системы (они изображены овалами) называются вершинами графа. Связи между элементами изображаются на графе линиями. Если линия направленная (т. е. со стрелкой), то она называется дугой. Если нет стрелки, то это ребро. Две вершины, соединенные ребром или дугой, называются смежными.
Разберемся, почему граф на рис. 2.9 содержит ненаправленные линии. Всякая связь имеет определенный смысл, ее можно как-то назвать. На нашем графе связи называются: «соединены дорогой». Понятно, что если поселок А соединен дорогой с поселком Б, то, значит, и Б соединен с А. Здесь не может быть односторонней связи.
Такие связи называются симметричными. Симметричные связи на графе — это ребра.
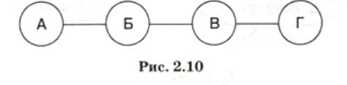
Простейшей структурой системы является линейная структура. Если, например, населенные пункты А, Б, В, Г расположены вдоль одной дороги, то система дорожной связи между ними имеет линейную структуру (рис. 2.10).
А теперь рассмотрим пример системы с несимметричными связями. Изобразим в форме графа систему, состоящую из двух человек: отца (его зовут Лев) и сына (Андрей):
Стрелка (дуга) отражает связь «быть отцом». В таком случае ясно, что справедлив факт «Лев является отцом Андрея», но не наоборот. Этот факт и представлен на графе.
