Урок 6
Алфавитный подход к измерению количества информации
§ 1.3. Количество информации
Содержание урока
1.3.3. Алфавитный подход к определению количества информации
Лабораторная работа № 3 «Учимся вычислять количество информации»
1.3.3. Алфавитный подход к определению количества информации
При алфавитном подходе к определению количества информации отвлекаются от содержания (смысла) информации и рассматривают информационное сообщение как последовательность знаков определенной знаковой системы.
Информационная емкость знака. Представим себе, что необходимо передать информационное сообщение по каналу передачи информации от отправителя к получателю (рис. 1.13). Пусть сообщение кодируется с помощью знаковой системы, алфавит которой состоит из N знаков {1, ..., N}. В простейшем случае, когда длина кода сообщения составляет один знак, отправитель может послать одно из N возможных сообщений: 1, 2, ..., N, которое будет нести количество информации I.
Рис. 1.13. Передача информации
Формула (1.1) связывает между собой количество возможных информационных сообщений N и количество информации I, которое несет полученное сообщение. В рассматриваемой ситуации N — это количество знаков в алфавите знаковой системы, а / — количество информации, которое несет каждый знак:
N = 21.
С помощью этой формулы можно, например, определить количество информации, которое несет один знак в двоичной знаковой системе:
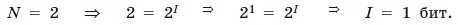
Таким образом, в двоичной знаковой системе знак несет 1 бит информации. Интересно, что сама единица измерения количества информации «бит» (bit) получила свое название от английского словосочетания «Binary digiT» — «двоичная цифра».
Информационная емкость знака двоичной знаковой системы составляет 1 бит.
Чем большее количество знаков содержит алфавит знаковой системы, тем большее количество информации несет один знак. В качестве примера определим количество информации, которое несет буква русского алфавита. В русский алфавит входят 33 буквы, однако на практике часто для передачи сообщений используются только 32 буквы (исключается буква «ё»).
С помощью формулы (1.1) определим количество информации, которое несет одна буква русского алфавита:
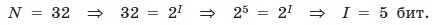
Таким образом, буква русского алфавита несет 5 битов информации.
Количество информации, которое несет знак, зависит от вероятности его получения. Если получатель заранее точно знает, какой знак придет, то полученное количество информации будет равно 0. Наоборот, чем менее вероятно получение знака, тем больше его информационная емкость.
В русской письменной речи частота использования букв в тексте различна. Так, в среднем на 1000 знаков осмысленного текста приходится 200 букв «а» и в 100 раз меньшее количество буквы «ф» (всего 2). Таким образом, с точки зрения теории информации, информационная емкость знаков русского алфавита различна (у буквы «а» она наименьшая, а у буквы «ф» — наибольшая).
Количество информации в сообщении. Сообщение состоит из последовательности знаков, каждый из которых несет определенное количество информации.
Если знаки несут одинаковое количество информации, то количество информации IС в сообщении можно подсчитать, умножив количество информации I, которое несет один знак, на длину кода (количество знаков в сообщении) К:
IС = I • К. (1.2)
Так, каждая цифра двоичного компьютерного кода несет 1 бит информации. Следовательно, две цифры несут 2 бита информации, три цифры — 3 бита и т. д. Количество информации в битах равно количеству цифр двоичного компьютерного кода (табл. 1.3).
Таблица 1.3. Количество информации,
которое несет двоичный компьютерный код
Задания для самостоятельного выполнения
1.8. Задание с выборочным ответом. Какое количество информации содержит один разряд двоичного числа?
1) 1 байт
2) 3 бита
3) 4 бита
4) 1 бит
1.9. Задание с кратким ответом. Какое количество информации несет двоичный код 10101010?
1.10. Задание с кратким ответом. Какова информационная емкость знака генетического кода?
Cкачать материалы урока
