Урок 22
Электронные таблицы. Основные возможности

§ 4.2. Электронные таблицы

Содержание урока

4.2.3. Относительные, абсолютные и смешанные ссылки

4.2.4. Встроенные функции

Практическая работа 4.3

Лабораторная работа № 14 «Строим графики и диаграммы в электронных таблицах»

4.2.4. Встроенные функции

Формулы могут включать в себя не только адреса ячеек и знаки арифметических операций, но и функции. Электронные таблицы имеют несколько сотен встроенных функций, которые подразделяются на категории: Математические, Статистические, Финансовые, Дата и время и т. д.

Суммирование. Одной из наиболее часто используемых операций является суммирование значений диапазона ячеек. Для суммирования значений диапазона, расположенных в одном столбце или строке, достаточно выделить этот диапазон и вызвать функцию суммирования чисел СУММ(), щелкнув по кнопке Σ Автосумма на панели инструментов Формулы.

Результат суммирования будет записан в ячейку, следующую за последней ячейкой диапазона в столбце (например, =СУММ(А2:А4)), строке (например, =СУММ(С1:Е1)) (рис. 4.4).

При суммировании значений ячеек выделенный диапазон можно откорректировать путем перемещения границы диапазона с помощью мыши или введением в формулу адресов ячеек с клавиатуры.

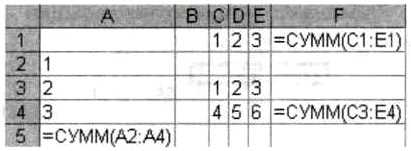
Рис. 4.4. Суммирование значений диапазонов ячеек

Степенная функция. В математике широко используется степенная функция у = хⁿ, где х — аргумент, а n — показатель степени (например, у = х², у = х³ и т. д.). Ввод функций в формулы можно осуществлять с помощью клавиатуры или с помощью средства Вставить функцию (Мастер функций), которое предоставляет пользователю возможность вводить функции с использованием последовательностей диалоговых окон.

Например, если в ячейке В1 хранится значение аргумента х функции, то вид функции х², введенной с клавиатуры (ячейка В2), будет =В1ˆ2, а введенной с помощью Мастера функций (ячейка ВЗ) — СТЕПЕНЬ(В1;2) (рис. 4.5).

Рис. 4.5. Степенная функция у = х²

Квадратный корень. Квадратный корень является степенной функцией с дробным показателем, где n = 1/2. Записывается эта функция обычно с использованием знака квадратного корня .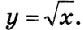

Например, если в ячейке В1 хранится значение аргумента функции х, то вид функции 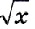, введенной с клавиатуры (ячейка В2), будет =В1ˆ(1/2), а введенной с помощью Мастера функций (ячейка ВЗ) — КОРЕНЬ(В1) (рис. 4.6).

Рис. 4.6. Квадратный корень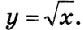

Таблица значений функции. В электронных таблицах можно не только вычислить значение функции для любого заданного значения аргумента, но и представить функцию в форме таблицы числовых значений аргумента и вычисленных значений функции.

Заполнение таблицы можно существенно ускорить, если использовать операцию Заполнить. Сначала в первую ячейку строки аргументов вводится наименьшее значение аргумента (например, в ячейку В1 вводится число -4), а во вторую ячейку вводится формула, вычисляющая следующее значение аргумента с учетом величины шага аргумента (например, =B1+1) (табл. 4.7). Далее эта формула вводится во все остальные ячейки таблицы с использованием операции Заполнить вправо.

Аналогично, в первую ячейку строки значений функции вводится формула вычисления функции (например, в ячейку В2 вводится формула =В1ˆ2), далее эта формула вводится во все остальные ячейки таблицы с использованием операции Заполнить вправо (см. табл. 4.7).

Таблица 4.7. Числовое представление квадратичной функции у = х²

Задания для самостоятельного выполнения

4.10. Задание с кратким ответом. Какие значения будут получены в ячейках А5 и F1 после суммирования диапазонов ячеек (см. рис. 4.4)? Проверьте в электронных таблицах.

4.11. Задание с кратким ответом. Какие значения будут получены в ячейках В2 и ВЗ после вычисления значений степенной функции (см. рис. 4.5)? Проверьте в электронных таблицах.

4.12. Задание с кратким ответом. Какие значения будут получены в ячейках В2 и ВЗ после вычисления значений квадратного корня (см. рис. 4.6)? Проверьте в электронных таблицах.

Cкачать материалы урока