Урок 3
Моделирование в среде графического редактора
Представление о моделировании в среде графического редактора
 |
 |
 |
|
|
|
Некоторые думают, что использование моделей началось недавно. Однако само по себе моделирование старо как мир. Оно появилось тогда, когда человечество осознало свое место в окружающем мире и стало стремиться к пониманию и изменению его.
Одной из разновидностей моделей являются геометрические модели. Они передают внешние признаки объекта: размеры, форму, цвет. Геометрические модели представляют собой некоторые объекты, геометрически подобные своему прототипу (оригиналу). Они служат, в основном, для учебных и демонстрационных целей, используются при проектировании сооружений, конструировании различных устройств и изделий. Простейшие модели такого типа окружают вас с раннего детства — это игрушки. С возрастом вы сталкиваетесь со все более сложными геометрическими моделями. Изучая биологию, вы пользуетесь чучелами или макетами животных, скелетом человека с шарнирами вместо суставов для демонстрации движения рук и ног. Макет здания, корабля, скульптура, рисунок — все это геометрические модели. Приступая к созданию таких моделей, следует выделить объект, определить цели моделирования, сформировать информационную модель объекта в соответствии с поставленной целью и выбрать инструмент моделирования.
В среде графического редактора, который является удобным инструментом для построения геометрических моделей, мы создаем графические объекты — рисунки. Любой рисунок, с одной стороны, является моделью некоторого оригинала (реального или мысленного объекта), а с другой стороны — объектом среды графического редактора.
В среде графического редактора очень важно научиться создавать обобщенную информационную модель графического объекта, которая представлена в таблице 1.1.
Таблица 1.1. Информационная модель графического объекта
Как видно из таблицы, важнейшими характеристиками, отражаемыми в геометрической модели объекта, являются размеры и пропорции. Для построения компьютерных моделей следует решить следующие задачи:
♦ моделирование геометрических операций, обеспечивающих точные построения в графическом редакторе;
♦ моделирование геометрических объектов с заданными свойствами, в частности, формой и размерами.
В этом разделе вы познакомитесь с разнообразием геометрических моделей, создаваемых в графическом редакторе, и сферами применения этих моделей. Геометрические модели отличает простота и наглядность, а среда, которая выбрана для моделирования, доступна даже неподготовленному пользователю.
При создании геометрических моделей следует придерживаться этапов моделирования, рассмотренных в учебнике «Информатика. Базовый курс. Теория» в разделе «Информационная картина мира». Соблюдение этих этапов — гарантия достижения цели. Иногда опыт, здравый смысл и знания помогут вам легко решить любую проблему без детального описания этапов моделирования.
Моделирование геометрических операций и фигур
ЗАДАЧА 1.1. Моделирование геометрических операций
I этап. Постановка задачи
ОПИСАНИЕ ЗАДАЧИ
Вся история геометрии связана с практикой построений при помощи подручных средств для измерения недоступного. В Древнем Египте, задолго до доказательства Пифагором его знаменитой теоремы, использовали треугольник со сторонами, соотносящимися как 3:4:5, для получения прямых углов в строительстве. Фалесу Милетскому, жившему в VI в. до н. э., приписывается метод измерения расстояния до кораблей, находящихся в море, с использованием признаков подобия треугольников.
К задачам, поставленным еще в древности, относятся задачи деления отрезков и углов на две равные части. Их решение было известно еще в догреческий период (V в. до н. э.).
Построения в графическом редакторе и на листе бумаги несколько отличаются, потому что компьютерные инструменты не совсем идентичны привычным, повседневным. Например, графический редактор не имеет линейки, в нем нет инструмента, подобного транспортиру, в окружности, нарисованной в графическом редакторе, не определен центр. Поэтому необходимо научиться строить модели геометрических операций: деление отрезка и угла на равные части, определение центра окружности и др. Это можно сделать, используя законы геометрии.
ЦЕЛЬ МОДЕЛИРОВАНИЯ
При отсутствии специальных инструментов (линейки, транспортира, циркуля) смоделировать основные геометрические операции.
ФОРМАЛИЗАЦИЯ ЗАДАЧИ
Исходные геометрические объекты (отрезок, радиус, угол) задаются в левом верхнем углу рабочего поля. Для построений используются их копии. Построение основывается на законах геометрии.
II этап. Разработка модели
МОДЕЛЬ 1. Деление отрезков (моделирование функций линейки)
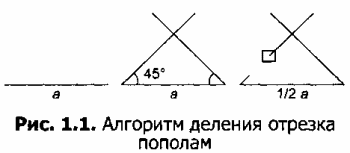
Алгоритм деления отрезка пополам приведен на рисунке 1.1. Построение основано на том, что высота в равнобедренном треугольнике является одновременно биссектрисой и медианой. Для построения достаточно инструмента Линия и клавиши Shift.
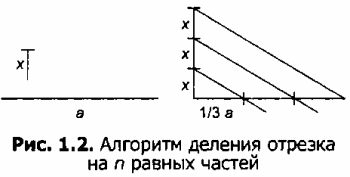
Алгоритм деления отрезка на n равных частей (для n = 3) приведен на рисунке 1.2. Для выполнения операции деления используется отрезок произвольной длины х. Построение основано на подобии треугольников. Параллельность линий достигается копированием.
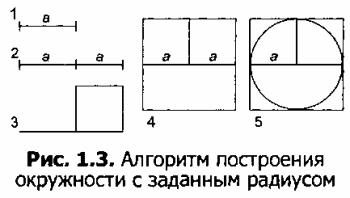
МОДЕЛЬ 2. Построение окружности заданного радиуса и определение ее центра (моделирование функций циркуля)
Окружность в графическом редакторе вписывается в квадрат со стороной, равной удвоенному радиусу. Алгоритм построения окружности изображен на рисунке 1.3.
МОДЕЛЬ 3. Деление угла пополам (моделирование функции транспортира)
На рисунке 1.4 приведен один из вариантов алгоритма деления.
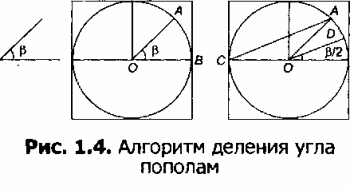
В качестве дополнительного построения используется окружность любого радиуса. В ее центр помещается копия угла, подлежащего делению. Углы АОВ и АСВ относятся как 2:1 (докажите это). Отсюда, если линия DO параллельна линии АС, то она является биссектрисой заданного угла. Построение сводится к копированию части отрезка АС и установке его копии к точке О. Полученная параллельная линия DO разделит заданный угол пополам.
III этап. Компьютерный эксперимент
ПЛАН ЭКСПЕРИМЕНТА
1. Тестирование построенной по заданному алгоритму модели 1 совмещением отрезков, полученных при делении.
2. Тестирование построенной по заданному алгоритму модели 2 совмещением исходного и повернутого на 90° отрезка с радиусами полученной окружности.
ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ
Докажите правильность алгоритмов построения.
IV этап. Анализ результатов
Если результаты тестирования отрицательные, увеличить точность выполнения алгоритма за счет работы в увеличенном масштабе (под лупой).
ЗАДАЧА 1.2. Моделирование объектов с заданными геометрическими свойствами
I этап. Постановка задачи
ОПИСАНИЕ ЗАДАЧИ
Задачи на построение возникли в глубокой древности и были связаны с практическими потребностями. Примеры из истории развития геометрии свидетельствуют, что можно добиться точности, даже если под рукой нет специальных измерительных инструментов, а есть подсобные предметы: кусок веревки, ровная палочка и т. п.
Поэтому необходимо научиться строить модели геометрических фигур с заданными свойствами: равносторонний треугольник, шестиугольник, равнобедренный треугольник и пр. Это можно сделать, используя законы геометрии.
ЦЕЛЬ МОДЕЛИРОВАНИЯ
В среде графического редактора научиться моделировать геометрические объекты с заданными свойствами.
ФОРМАЛИЗАЦИЯ ЗАДАЧИ
Геометрическая фигура характеризуется длиной сторон и углами, которые необходимо задать в виде отрезков и углов на рабочем поле графического редактора перед началом построения.
II этап. Разработка модели
МОДЕЛЬ 4. Построение равностороннего треугольника с заданной стороной
Данный алгоритм предложил Евклид в IV в. до н. э. Построить треугольник по алгоритму, приведенному на рисунке 1.5, и доказать, что полученный треугольник действительно правильный.
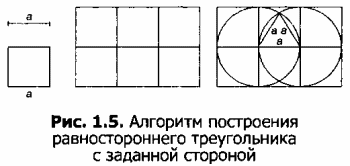
МОДЕЛЬ 5. Построение правильного шестиугольника с заданной стороной
Используя свойство правильных фигур вписываться в окружность и то, что сторона равностороннего шестиугольника равна радиусу описанной окружности, выполнить построение по алгоритму на рисунке 1.6.
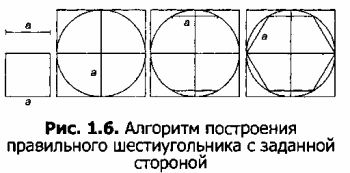
Начать построение окружности с радиусом, равным заданной стороне шестиугольника.
III этап. Компьютерный эксперимент
ПЛАН ЭКСПЕРИМЕНТА
1. Тестирование построенной по заданному алгоритму модели совмещением с исходными отрезками и углами.
2. Построение и тестирование модели по собственному алгоритму с теми же исходными данными.
3. Исследование и анализ двух алгоритмов построения с целью определения наилучшего.
ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ
1. Докажите правильность приведенного и собственного алгоритмов для каждой модели.
2. Совместите построения, выполненные по разным алгоритмам.
IV этап. Анализ результатов
Если при совмещении фигуры не совпали, то изменить алгоритм построения или увеличить точность выполнения алгоритма за счет работы в увеличенном масштабе (под лупой). Если совпали, то выберите наиболее удобный алгоритм.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1.3. Построить равнобедренный треугольник по заданному основанию а и высоте h по нижеприведенному или собственному алгоритму. Высота в равнобедренном треугольнике одновременно является и медианой. Построение сводится к повороту отрезка, задающего высоту, на 90° и к делению отрезка, задающего основание, пополам. Алгоритм построения представлен на рисунке 1.7.
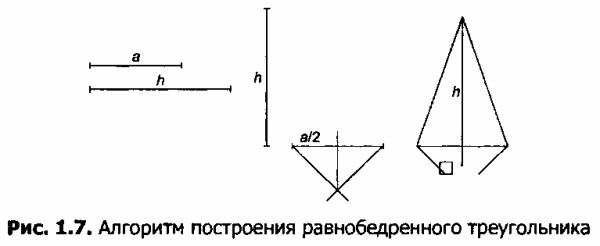
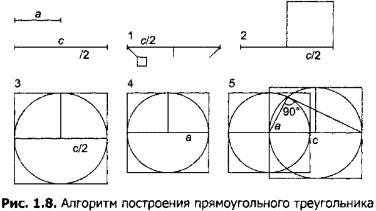
1.4. Построить прямоугольный треугольник по гипотенузе и катету. Построение произвести по нижеприведенному или собственному алгоритму. Угол, вписанный в окружность и опирающийся на диаметр, равен 90°. Приведенный на рисунке 1.8 алгоритм основан на построении двух окружностей: с диаметром, равным заданной гипотенузе, и с радиусом, равным заданному катету.
1.5. Построить равнобедренный треугольник по боковой стороне и углу при вершине. Построение произвести по собственному алгоритму.
1.6. Построить треугольник по трем сторонам.
1.7. Построить правильный восьмиугольник с заданной стороной.
1.8. Построить треугольник по двум сторонам и углу между ними.
1.9. Построить параллелограмм по заданным сторонам и острому углу.
