Урок 13
Основы алгоритмизации

Существует одно условие, при котором компьютер «оживает» и все его блоки начинают выполнять предусмотренные действия. Это наличие в нем программ, которые заставляют компьютер работать, выполнять всевозможные операции по вводу, преобразованию, сохранению и выводу информации. Программы являются «душой» компьютера. Они предоставляют человеку среду и технологический инструментарий для создания текстовых документов, выполнения сложных расчетов, хранения больших массивов данных, компьютерных развлечений и т. д.

Все программы, находящиеся в компьютере, получили название программного обеспечения. Для эффективного использования программного обеспечения надо уметь структурировать информацию и разрабатывать для ее обработки алгоритмы, знать возможности каждой программы, когда и как их применять, владеть технологией работы в выбранной программной среде.

В этом разделе вы узнаете о назначении и возможностях трех классов программного обеспечения: системного, прикладного и инструментария программирования. В качестве примера системной среды рассматривается операционная система Windows. При изучении прикладных сред будет использован объектный подход. Вы познакомитесь с общими и отличительными характеристиками прикладных сред общего назначения: графическим редактором, текстовым и табличным процессорами, системой управления базой данных. Для понимания технологии работы с инструментарием программирования вы должны научиться составлять алгоритм решения поставленной задачи, чему и будет посвящена одна из тем. Непосредственно же программная среда, в качестве которой выбрана среда ЛОГО, будет изучаться в практикуме.

Сведения о программном обеспечении в этом разделе излагаются с теоретических позиций. Поэтому изучение всех тем должно идти параллельно с практическим освоением технологии разработки алгоритмов и технологии работы в системной среде, в прикладных средах общего назначения, в среде программирования на основе учебного пособия «Информатика и ИКТ. Практикум. 8-9 класс».

Алгоритмы

Изучив эту тему, вы узнаете:

- назначение алгоритма и его основные свойства;
- формы представления алгоритма;
- типовые алгоритмические конструкции и виды алгоритмов;
- разновидности циклических алгоритмов и их особенности;
- назначение вспомогательных алгоритмов;
- основные стадии создания алгоритма.

12.1. Понятие алгоритма

С самого детства вы сталкиваетесь с алгоритмами, не осознавая этого. Алгоритмы появляются в ситуациях, которые можно описать в виде последовательности действий.

Например, с утра вас призывает радио «На зарядку становись!» Вам предлагается выполнить одно из упражнений в следующей последовательности:

Рассмотрим еще пример. Вы решили зайти к другу, а у него в подъезде установлен домофон. Вы выполняете действия, следуя инструкции, вывешенной на входной двери:

В первом примере вашими действиями управляет спортивный инструктор по радио. Во втором случае вы сами в соответствии с инструкцией управляете техническим устройством (домофоном), с помощью которого осуществляется голосовая связь и дистанционное открытие двери. В обоих случаях вы совершаете заданную последовательность действий для достижения определенной цели. А если вместо вас будет кто-то другой, сможет ли он выполнить то, что делали вы? Конечно сможет, ведь эти инструкции адресованы любому человеку.

Из этого можно сделать важный вывод: «Строго следуя плану, любой человек, не знакомый ранее с описанной в плане последовательностью действий, получит ожидаемый результат».

Подробное описание действий, необходимых для получения ожидаемого результата, получило название алгоритма. С этим понятием вы сталкиваетесь постоянно.

- В кулинарных книгах собраны рецепты приготовления разных блюд.
- Любой прибор, купленный в магазине, снабжается подробной инструкцией.
- В журналах мод есть выкройки и описания, руководствуясь которыми можно сшить одежду.
- В популярных изданиях приводятся алгоритмы развития памяти, улучшения зрения.
- В школьных учебниках приводятся алгоритмы решения типовых задач.

Появление алгоритмов связывают с зарождением математики. Более 1000 лет назад (825 г.) ученый из города Хорезма Абдулла (или Абу Джафар) Мухаммед бен Муса аль-Хорезми создал книгу по математике, в которой описал способы выполнения арифметических действий над многозначными числами. Эти способы и сейчас изучают в школе. Само слово «алгоритм» возникло в Европе после перевода на латынь книги этого среднеазиатского математика, в которой его имя писалось как «Алгоритмы». «Так говорил Алгоритми», — начинали европейские ученые, ссылаясь на правила, предложенные Мухаммедом аль-Хорезми.

Научное определение понятия алгоритма дал А. Черч в 1930 году. Позже и другие математики вносили свои уточнения в это определение. В школьном курсе информатики вы будете пользоваться следующими определениями.

    Алгоритм — описание последовательности действий (план), исполнение которых приводит к решению поставленной задачи за конечное число шагов.

    Алгоритмизация — процесс разработки алгоритма (плана действий) для решения задачи.

Область математики, известная как теория алгоритмов, посвящена исследованию свойств, способов записи и сферы применения различных алгоритмов, а также созданию новых алгоритмов. Учеными всего мира накоплена уникальная коллекция алгоритмов обработки информации. Эта коллекция все время пополняется.

Теория алгоритмов находит применение в различных сферах деятельности человека. Появление компьютеров внесло свою лепту в эту теорию. Алгоритмы, реализованные на компьютере, позволили решать сложные задачи в различных областях, например:

- в медицине — автоматическая диагностика и обработка данных компьютерной томографии;
- в производстве — управление техническими устройствами, заменяющими человека в сложных или опасных для жизни условиях;
- в кинематографии — обработка изображений, моделирование пейзажей и движений, сжатие видео- и аудиоинформации;
- в Интернете — увеличение скорости поиска и обработки данных поисковыми системами;
- в аэрокосмонавтике — управление космическими кораблями и спутниками;
- в сфере безопасности — распознавание «свой-чужой» и т. д.

12.2. Свойства алгоритмов

Мир алгоритмов очень разнообразен. Мы часто не замечаем, что используем алгоритмы, выполняя привычные действия механически, не задумываясь. Можно выделить общие свойства, которыми должен обладать любой алгоритм независимо от того, к какой сфере деятельности или области знаний он относится и кто его выполняет.

Мы будет вас знакомить последовательно с каждым из этих свойств, рассматривая различные примеры.

Пример 12.1

Представьте, что вы отправились с друзьями в туристический поход. Кто-то из вас умеет без труда разжигать костер в лесу. Но в вашей компании есть и новички, которым нужно рассказать или показать, как это делается. Алгоритм разжигания костра при хорошей погоде можно найти в справочнике туриста.

Алгоритм «Разжигание костра при хорошей погоде»

В приведенном алгоритме четко указываются как сами действия, так и порядок их выполнения. Попробуйте поменять местами пункты 1 и 2. Ничего страшного не произойдет, но с хворостом в руках искать место для костра или перекладывать хворост с одного места на другое неудобно.

Приведенный алгоритм обладает свойством дискретности (от лат. discretus — разделенный, прерывистый). Это свойство предполагает, что любой алгоритм должен состоять из последовательности шагов, следующих друг за другом. Следующий шаг выполняется только после завершения предыдущего.

Пример 12.2

Представьте, что вам нужно сварить кашу на костре в котелке. У вас заранее приготовлено приспособление для того, чтобы повесить котелок над костром. Сначала надо разжечь костер, а затем приступить к варке каши. В том же справочнике туриста приводится рецепт варки гречневой каши и нормы расхода крупы на одну порцию.

Алгоритм «Приготовление гречневой каши»

По форме представления этот алгоритм ничем не отличается от предыдущего. Он обладает свойством дискретности, поскольку представляется в виде последовательности заранее определенных действий. Однако каша по этому алгоритму получится не у всех. В пункте 7 этого алгоритма соль добавляется по вкусу. У неопытного повара этот пункт вызовет сложности. То же самое можно сказать о пункте 10: не каждый знает, как убавить огонь в костре. Кто-то может подумать, что нужно снять котелок и подождать, пока дрова прогорят и огонь станет меньше.

Чтобы устранить эту неопределенность, в алгоритм следует внести изменения:

- в пункте 7 указать расход соли из расчета на одну порцию;
- в пункт 10 добавить уточнение «сдвинув котелок от центра костра к краю».

Теперь этим алгоритмом может воспользоваться любой человек, так как он обладает свойством детерминированности (от лат. determinate — определенность, точность). Это свойство указывает, что любое действие в алгоритме должно быть строго и недвусмысленно определено и описано для каждого случая.

    ОБРАТИТЕ ВНИМАНИЕ

Рассмотренный в примере 12.1 алгоритм «Разжигание костра при хорошей погоде» также обладает свойством детерминированности, так как все действия однозначно определены и отсутствует неопределенность в их выполнении.

Пример 12.3

Предположим, в походе вам понадобилось узнать расстояние до ближайшего населенного пункта. Для решения этой задачи необходима информация о примерной высоте различных объектов (окна, столба, человека и пр.), а также усредненное значение длины руки взрослого и ребенка. Тогда можно будет воспользоваться приведенным в том же справочнике туриста алгоритмом определения расстояния до предмета.

Алгоритм «Определение расстояния»

Этот алгоритм основан на свойствах подобных треугольников, и при желании вы можете это проверить.

Данный алгоритм обладает свойством дискретности и свойством детерминированности, так как все действия представляются в виде последовательности, однозначно определены и отсутствует неопределенность в их выполнении.

А как быть, если нет линейки? Вместо линейки в качестве подручного средства может быть использована спичка, карандаш, прямая палка или любой другой предмет, на который предварительно нанесены деления. Учитывая это, в алгоритме вместо слова «линейка» следует поставить обобщающее слово, например «палка с делениями» или «дальномер».

Уточненный алгоритм позволяет решить множество похожих задач — по нему можно измерить расстояние до любого видимого предмета при помощи любой палки с делениями.

Про такой алгоритм говорят, что он обладает свойством массовости. Это свойство подразумевает, что один и тот же алгоритм может применяться для решения целого класса задач, отличающихся исходными данными. Исходные данные должны выбираться из множества допустимых значений для данного алгоритма. Элементами этого множества могут быть числа, слова, геометрические фигуры, химические вещества, технические приборы, продукты питания и т. д.

Свойство массовости подразумевает использование переменных в качестве исходных данных алгоритма.

    ОБРАТИТЕ ВНИМАНИЕ

Рассмотренный в примере 12.1 алгоритм «Разжигание костра при хорошей погоде» также обладает свойством массовости, так как в качестве исходных данных здесь используются сухие ветки (любых деревьев) и любой источник огня (спички, зажигалка, лупа и пр.)

Рассмотренный в примере 12.2 рецепт приготовления гречневой каши не может быть использован для приготовления каши из другой крупы. Однако по нему может быть приготовлено разное количество порций. В данном случае количество порций — исходные данные для алгоритма «Приготовление гречневой каши». В рамках этих исходных данных алгоритм обладает свойством массовости.

Пример 12.4

Продолжая туристическую тематику, представим, что в походе двое заядлых рыбаков принесли неплохой улов. Необходимо написать алгоритм определения победителя с учетом свойства массовости. Для этого следует представить алгоритм в общем виде и ввести переменные:

- В1 — вес рыбы, пойманный первым рыбаком;
- В2 — вес рыбы, пойманный вторым рыбаком.

Алгоритм «Кто победил»

По этому алгоритму можно определить победителя не только в рыбалке, но и в собирании грибов, ягод и пр.

При всей простоте и очевидности алгоритма не каждый сразу поймет его ошибочность. В этом алгоритме не рассмотрена ситуация равенства чисел В1 и В2, которую следует учесть, добавив в алгоритм еще один пункт:

5. Если число В1 равно числу В2, то сообщите: «победила дружба».

В уточненном алгоритме рассмотрены все возможные ситуации и для каждой из них получен результат. В таких случаях говорят, что алгоритм обладает свойством результативности.

Конечной целью любого алгоритма является получение результата, поэтому свойство результативности очень важное. Если результат по каким-либо причинам отсутствует, об этом следует сообщить.

    ОБРАТИТЕ ВНИМАНИЕ

Рассмотренный в примере 12.1 алгоритм «Разжигание костра при хорошей погоде» обладает свойством результативности, так как изначально он был разработан только для хороших погодных условий, при которых костер всегда будет разожжен.

Рассмотренный в примере 12.2 алгоритм «Приготовление гречневой каши» обладает свойством результативности, так как ориентирован только на приготовление определенного сорта каши.

Рассмотренный в примере 12.3 алгоритм «Определение расстояния» обладает свойством результативности, так как мы всегда можем измерить расстояние.

Из свойства результативности следует свойство конечности алгоритма, которое определяет завершение каждого действия в отдельности и алгоритма в целом за конечное число шагов.

Для иллюстрации этого свойства вспомним рассмотренную ранее инструкцию пользования домофоном. Предположим, вы пришли к другу, а дома никого нет. Действуя строго по инструкции, вы так и будете стоять у дверей, дожидаясь ответа.

Этот алгоритм не обладает свойством конечности и его следует доработать. Сделайте это самостоятельно.

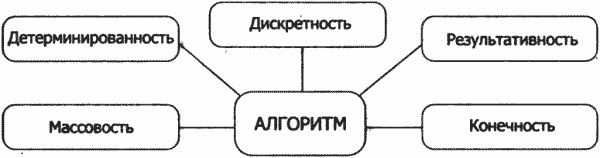
Обобщим выводы всех рассмотренных примеров. Алгоритм характеризуется следующими свойствами:

- дискретностью;
- детерминированностью;
- массовостью;
- результативностью;
- конечностью.

12.3. Формы представления алгоритма

Алгоритм может быть представлен в различных формах: словесной, графической, табличной, программной. На рисунке 12.1 приведены возможные способы представления алгоритмов.

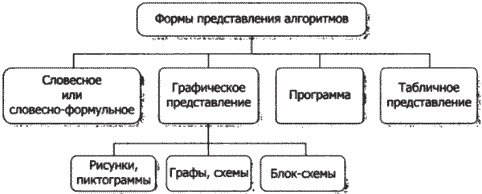
Рис. 12.1. Формы представления алгоритма

Приведенные ранее алгоритмы были представлены в виде описания последовательности действий, то есть в словесной форме.

Такой способ представления несложен, но имеет недостатки. Главный недостаток состоит в том, что при таком способе допускается некоторая произвольность изложения, нет четких стандартов описания. Сложные задачи с анализом условий, с повторяющимися действиями и возвратами к предыдущим пунктам трудно представляются в словесном и словесно-формульном виде.

Преимуществом графического способа представления является его наглядность.

Одной из форм графического представления являются рисунки. Примеры представления алгоритмов в виде рисунков вы можете увидеть на упаковках продуктов быстрого приготовления, в инструкциях по использованию бытовой техники и пр.

Можно представить алгоритм в виде схемы или графа — это более строгая, формализованная форма.

На рисунке 12.2 представлен в виде схемы алгоритм решения математической задачи о разрезании торта на куски тремя движениями ножа таким образом, чтобы каждому досталась розочка.

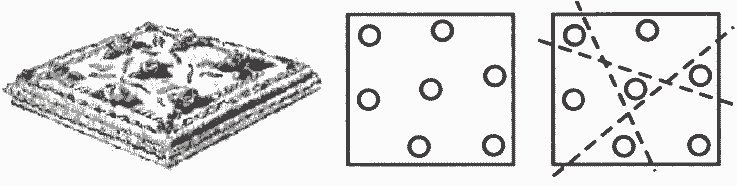
Рис. 12.2. Алгоритм решения задачи в виде схемы

В виде графа удобно представлять алгоритмы решения логических задач, задач по комбинаторике и пр. На рисунке 12.3 представлен алгоритм «Разбор предложения» в виде графа.

Граф — геометрический объект, состоящий из вершин и соединяющих вершины линий-дуг. В алгоритме анализа структуры предложения вершинами являются члены предложения, дуги показывают связи членов предложения, направления дуг — последовательность анализа (порядок действий алгоритма).

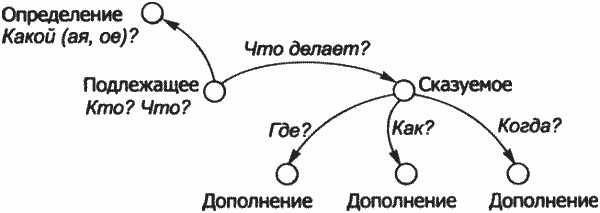
Рис. 12.3. Алгоритм решения задачи в виде графа

Если алгоритм предназначен для исполнения техническим устройством, например станком с числовым программным управлением или компьютером, он представляется в виде программы. В школе часто используется форма представления алгоритма в виде программы на школьном алгоритмическом языке.

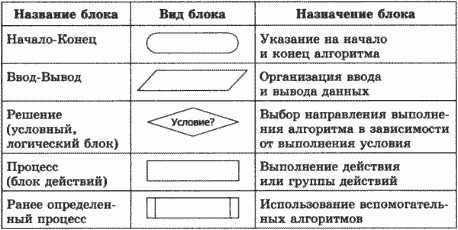
Наиболее распространенной формой представления алгоритма является блок-схема. Для отображения алгоритма в виде блок- схемы используется стандартный набор графических объектов (блоков), перечень и условные обозначения которых приведены в таблице 12.1. Использование блок-схем, состоящих из типового набора блоков, позволяет трактовать алгоритм однозначно.

Таблица 12.1. Стандартные графические объекты блок-схем

Приведем алгоритм решения задачи, представив его в разных формах.

Пример 12.5

Требуется рассчитать необходимое количество рулонов обоев для оклейки: комнаты. Заданы параметры комнаты: длина (а), ширина (b) и высота (h). Заданы параметры рулона обоев: длина (l), ширина (d). Считаем, что площадь окон и дверей составляет 15 % от площади стен.

Мы используем для представления алгоритма разные формы: словесно-формульное описание, блок-схему, программу.

Словесно-формульное описание алгоритма «Оклейка обоями» представляется в виде нумерованной последовательности действий, понятных человеку.

Алгоритм «Оклейка обоями»

Для описания алгоритма той же задачи может быть использована графическая форма представления, например в виде блок-схемы. Блок-схема, алгоритма «Оклейка обоями» так же как и словесная форма, должна быть понятна человеку, но в то же время в ней должна быть учтена специфика компьютера, которая часто связана с вводом исходных данных и выводом результатов.

Алгоритм «Оклейка обоями» представлен в виде блок-схемы на рисунке 12.4.

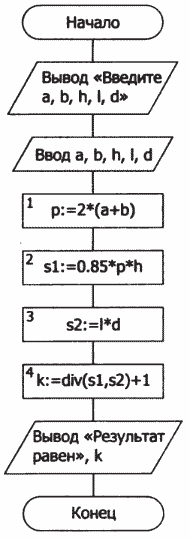
Рис. 12.4. Блок-схема

Пояснения к блок-схеме:

♦ действия, указанные в блоках 1-4, соответствуют действиям, указанным в словесном алгоритме в пп. 1-4;
♦ дополнительно введены блоки для ввода исходных данных в компьютер и вывода результата вычислений;
♦ дополнительно введены блоки начала и конца алгоритма.

Приведем форму представления того же алгоритма «Оклейка обоями» в виде программы на школьном алгоритмическом языке в таблице 12.2.

Таблица 12.2. Алгоритм «Оклейка обоями» в виде программы на школьном алгоритмическом языке

Все алгоритмы, приведенные в качестве примеров, имели одинаковую структуру: в них действия следовали одно за другим. Это самая простая разновидность алгоритмов. Но существуют алгоритмы, в которых последовательность действий может быть нарушена из-за выполнения или невыполнения некоторого условия. Встречаются алгоритмы, в которых некоторая последовательность действий повторяется, причем количество повторений тоже определяется условием.

Любой, даже самый сложный алгоритм, можно представить с помощью трех типовых конструкций (структур): последовательности, ветвления, цикла. Каждая структура имеет один вход и один выход.

На рисунке 12.5 представлены блок-схемы этих базовых структур, из которых видно, что:

♦ в структуре «последовательность» действия выполняются последовательно, сверху вниз, без возвратов (рис. 12.5, а);
♦ в структуре «ветвление» выполняется либо одна, либо другая группа действий в зависимости от истинности (выполнения) или ложности (невыполнения) условия (рис. 12.5, б);
♦ в структуре «цикл» действия повторяются до тех пор, пока выполняется заданное условие (рис. 12.5, в).

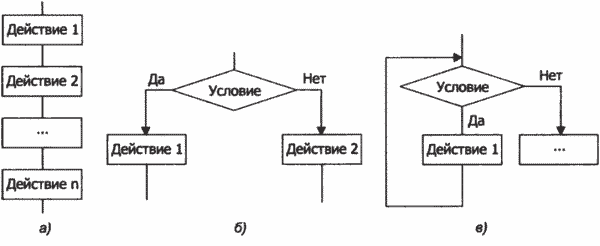
Рис. 12.5. Типовые алгоритмические структуры

Набор типовых структур часто называют алгоритмическими конструкциями, потому что из них, как из конструктора, можно составить алгоритм любой сложности.

В зависимости от того, какие базовые структуры использованы при составлении алгоритмов, различают три основные разновидности алгоритмов: линейный, разветвляющийся, циклический.