Урок 17
Прикладная среда табличного процессора Excel

Общая характеристика табличного процессора

Изучив эту тему, вы узнаете:

- каковы назначение и основные возможности текстового процессора;
- из каких элементарных объектов состоит табличный документ;
- какие типы данных могут храниться в ячейках таблицы;
- что такое абсолютная и относительная адресация;
- правила записи и копирования формул и функций;
- что такое диаграмма и из каких объектов она состоит.

Назначение табличного процессора

Табличный процессор содержит набор компьютерных инструментов для работы с информацией, представленной в табличной форме — в виде электронной таблицы. Рабочая область электронной таблицы напоминает по своей структуре шахматную доску. Она состоит из строк и столбцов, имеющих свои имена.

Основное назначение табличного процессора — автоматизация расчетов данных, представленных в табличной форме. Результатом работы табличного процессора является документ в виде таблицы или диаграммы.

Например, в табличном процессоре можно вести классный журнал. Учителя могут заносить в него оценки учащихся, а встроенные формулы позволят вычислить средний балл для каждого ученика, общую успеваемость класса по предмету и т. п. Каждый раз, когда учитель вносит новую оценку, табличный процессор будет автоматически пересчитывать все результаты.

Характерной особенностью табличного процессора является то, что в нем данные и результаты вычислений представлены в табличной форме. Для наглядности эти данные можно представить в графическом виде как диаграммы.

По сравнению со своей бумажной предшественницей электронная таблица предоставляет пользователю намного больше возможностей для работы. В клетки таблицы можно записывать не только числа, даты и тексты, но и логические выражения, функции и формулы. Формулы позволяют практически мгновенно производить пересчет и выводить в соответствующей ячейке новый результат при изменении исходных данных. Эта возможность позволяет активно использовать электронные таблицы в различных областях:

♦ для автоматизации вычислений;
♦ для представления результатов вычислений в виде диаграмм;
♦ для моделирования, когда исследуется влияние одних параметров на другие.

Объекты документа табличного процессора

Классификация объектов

Представление об объектах документа табличного процессора можно составить, познакомившись с их классификацией (рис. 4.1).

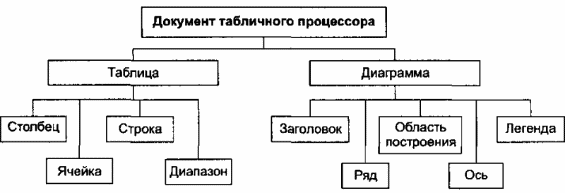
Рис. 4.1. Классификация объектов табличного документа

На первом уровне основанием классификации служит вид документа — таблица и диаграмма. Диаграмма является вспомогательным документом и без таблицы существовать не может. На втором уровне показаны основные объекты, которые образуют таблицу и диаграмму.

Объекты электронной таблицы

Таблица представляет собой сложный объект, состоящий из элементарных объектов: строк, столбцов, ячеек, диапазонов ячеек (рис. 4.2). Каждый элементарный объект имеет имя, которое определено разработчиками электронной таблицы.

Рис. 4.2. Элементарные объекты электронной таблицы

♦ Строка. Заголовки строк представлены в виде целых чисел, начиная с 1.
♦ Столбец. Заголовки столбцов задаются буквами латинского алфавита: сначала от А до Z, затем от АА до AZ, от ВА до BZ и т. д.
♦ Ячейка. Адрес ячейки определяется ее положением в таблице и образуется из заголовков столбца и строки, на пересечении которых она находится. Сначала записывается заголовок столбца, а затем номер строки, например: A3, D6, АВ46.
♦ Диапазон ячеек. Диапазон — это группа смежных ячеек: строка, несколько строк или часть строки; столбец, несколько столбцов или часть столбца; несколько смежных ячеек, образующих прямоугольную область. Диапазон ячеек задается указанием адресов его первой и последней ячеек, разделенных двоеточием.

Примеры:

• адрес ячейки, образованной пересечением столбца А и строки 7, — А7;
• адрес диапазона, образованного частью строки 3, — E3:G3;
• адрес диапазона, образованного частью столбца D, — D4:D8;
• адрес диапазона, имеющего вид прямоугольника с начальной ячейкой F5 и конечной ячейкой G8, — F5:G8.

Ячейка — элементарный объект электронной таблицы, расположенный на пересечении столбца и строки.

Строка — все ячейки, расположенные на одном горизонтальном уровне таблицы.

Столбец — все ячейки, расположенные в одном вертикальном ряду таблицы.

Диапазон ячеек — группа смежных ячеек, которая может состоять из строки, ее части или нескольких строк, столбца, его части или нескольких столбцов, а также из совокупности ячеек, охватывающих прямоугольную область таблицы; диапазоном можно также считать одну ячейку.

Таблица, создаваемая пользователем, представляет собой объект, характеризующийся определенным количеством строк и столбцов. Этому объекту присваивается имя, которое указывается в заголовке окна табличного документа. Над этим объектом можно производить действия, предусмотренные в табличном процессоре.

Параметры объектов таблицы представлены в табл. 4.1.

Таблица 4.1. Параметры объектов таблицы

Объекты диаграммы

Диаграмма является объектом электронной таблицы и предназначена для представления данных в графической форме. Данные, находящиеся в одном столбце или в одной строке, называют рядом. Перед построением диаграммы сначала необходимо указать ряды, а затем перейти к выбору типа диаграммы. Для характеристики диаграммы служат следующие параметры: имя, тип, область, размещение.

♦ Имя. Диаграмме дается имя, под которым она включается в состав электронной таблицы.

♦ Тип. Табличный процессор позволяет строить диаграммы различных типов. Основные типы диаграмм показаны на рис. 4.3. Рассмотрим подробнее некоторые из них.

   • График хорошо знаком вам по различным школьным задачам. На одном чертеже можно разместить несколько графиков, каждый из которых будет соответствовать своему ряду данных.

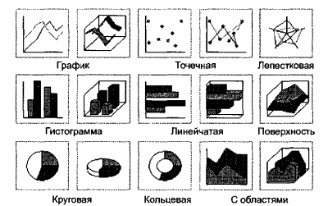
Рис. 4.3. Типы диаграмм

   • Гистограмма, или столбчатая диаграмма, в отличие от круговых, может быть построена для нескольких рядов данных. Высота каждого столбика определяется значением в соответствующей ячейке. Примером гистограммы может служить диаграмма распределения роста учеников каждого класса. Здесь каждый ряд представляет собой набор значений роста учеников каждого класса. Очевидно, что в электронной таблице каждый ряд занимает одну строку или один столбец.

   • Поверхностная диаграмма строится только для нескольких рядов и представляет собой группу многослойных разноцветных поверхностей. Каждый слой соответствует одному ряду данных.

   • Круговая диаграмма (плоская или объемная) используется для графического отображения одного ряда значений. Таким рядом может быть, например, набор значений роста или веса учащихся. Каждый сектор такой диаграммы отражает относительную (выраженную в процентах) долю каждого значения из ряда от общей суммы всех значений.

   • Смешанная диаграмма используется для отображения нескольких рядов данных с использованием разных типов диаграмм.

♦ Область. Ограничивает поле чертежа построения диаграммы.

♦ Размещение. Диаграмма может размещаться либо на том же листе, что и таблица, либо на отдельном листе. Диаграмма состоит из следующих объектов (рис. 4.4): ряд, ось, заголовок, легенда, область построения.

♦ Ряд. Диаграмма может быть построена как по одному ряду, так и по нескольким рядам. Для выделенного диапазона ячеек построение диаграммы ведется по нескольким рядам данных. В этом случае в качестве каждого ряда принимается соответствующая строка или столбец выделенного диапазона. Ряд может содержать подписи отображаемых значений.

♦ Ось. Каждая из осей диаграммы характеризуется следующими параметрами: вид, шкала, шрифт, число. 9 Вид определяет отображение внешнего вида оси на экране.

♦ Шкала определяет минимальное и максимальное значения шкалы, цену основных и промежуточных делений, точку пересечения с другими осями.

♦ Число определяет формат шкалы в соответствии с типами данных, находящихся в диапазоне.

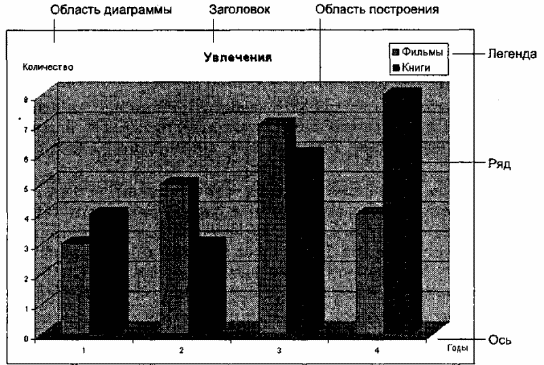
Рис. 4.4. Объекты диаграммы

♦ Заголовок. Заголовком служит текст, определяемый пользователем; как правило, заголовок размещается над диаграммой.

♦ Легенда. При выводе к диаграмме можно добавить легенду — список названий рядов (обозначений переменных).

♦ Область построения. Это область, ограниченная осями и предназначенная для размещения рядов данных. Для удобства анализа результатов на область построения может наноситься сетка.

Способы выделения объектов электронной таблицы

♦ Для выделения ячейки нужно щелкнуть на ней мышью или переместить на нее курсор с помощью клавиш управления курсором.

♦ Для выделения строки нужно щелкнуть на ее заголовке.

♦ Для выделения столбца нужно щелкнуть на его заголовке.

♦ Выделение диапазона ячеек может быть выполнено несколькими способами:
 
   • при помощи мыши — перемещая мышь при нажатой левой кнопке от начала к концу диапазона;
   • при помощи клавиш управления курсором — при нажатой клавише Shift;
   • вводом с клавиатуры начального и конечного адресов ячеек диапазона, разделенных двоеточием.

♦ Для выделения диаграммы необходимо выбрать диаграмму двойным щелчком мыши, а затем щелкнуть на нужном объекте.

Типовые действия над объектами электронной таблицы

Все действия над объектами электронной таблицы, кроме форматирования, редактирования и вычислений, выполняются так же, как и описанные ранее действия над объектами текстового документа. Технологии работы с инструментами табличного процессора аналогичны технологии работы в среде текстового процессора. Особенности действий, связанных с форматированием объектов, мы рассмотрим в теме 4.3.

Данные электронной таблицы

Общие сведения

В табличных процессорах предусмотрены различные форматы представления данных. Форматы определяют типы данных электронной таблицы: символьные (текстовые), числовые, логические, даты и т. д.

Так, например, для переноса разных продуктов человек использует разные емкости, контейнеры и т. п. Для того чтобы принести домой разливное молоко, вы используете бидон или банку, а не сумку или сетку. Если же вы отправились за картошкой, то вам понадобится как раз сетка или мешок, в то время как бидон и банка окажутся бесполезными. Яйца можно принести и в сетке, и в бидоне, но для повышения сохранности лучше воспользоваться специальным контейнером.

От того, какой формат выбран для той или иной ячейки, будет зависеть, какие действия табличный процессор сможет выполнять над ее содержимым.

Представьте себе, что в ячейку записаны цифры 120399. Как они будут восприняты табличным процессором? Какие действия будут над ними произведены? Если установлен текстовый формат, цифры будут восприняты как последовательность символов 1, 2, 0, 3, 9, 9. Если установлен числовой формат, они могут быть восприняты электронной таблицей как число. Если же ячейке назначен формат даты, они будут восприняты как 12 марта 1999 года.

Текстовый тип данных

Текстовые данные представляют собой некоторый набор символов. Если первый из них является буквой, кавычкой, апострофом или пробелом или если цифры в нем чередуются с буквами, то такая запись воспринимается как текст.

Действия над символьными данными производятся аналогично действиям над объектами в текстовом процессоре.

Примеры текстовых (символьных) данных:

Расписание занятий	8 «А» класс
"236	001 счет

Числовой тип данных

Числовые данные представляют собой последовательность цифр, которые могут быть разделены десятичной запятой и начинаться с цифры, знака числа (+ или -) или десятичной запятой. Над числовыми данными в электронной таблице могут производиться различные математические операции.

Примеры числовых данных:

232,5	,546
-13,7	+100

Запомните! Если в ячейке таблицы хранится последовательность цифр, начинающаяся с кавычки, то даже если такой набор цифр выглядит на экране как число, это — текст, и его нельзя использовать в вычислениях. Любые текстовые данные всегда воспринимаются как ноль. 

Укажем косвенный признак, по которому можно отличить текстовые и числовые данные. Если значение в ячейке после ввода распознано табличным процессором как текст, то по окончании ввода (после нажатия на клавишу Enter) они автоматически выравниваются по левой границе ячейки. Данные, распознанные как числовые, после ввода выравниваются по правой границе ячейки (рис. 4.5). Однако этот признак не является показательным, если выравнивание в ячейках было задано вручную.

Логический тип данных

Логические данные используются в логических формулах и функциях. Данные этого типа отображаются в ячейке следующим образом: если вводится любое отличное от нуля число (целое или дробное), то после нажатия на клавишу Enter в ячейке будет выведено значение Истина. Ноль отображается в соответствующей ячейке как Ложь.

Это представление данных связано с понятием логической переменной, которая используется в алгебре логики. Она служит для описания высказываний, которые могут принимать одно из двух возможных значений: «истина» (логическая единица) либо «ложь» (логический ноль).

Тип данных — даты

Этот тип данных используется при выполнении таких функций, как добавление к дате числа, вычисление разности двух дат или пересчет даты вперед или назад. Пересчет чисел в даты производится автоматически в зависимости от заданного формата. Табличный процессор позволяет представлять вводимые числа как даты несколькими способами.

Примеры представления дат в разных форматах:

12 апреля 2006	12.04.2006
Апрель 2006	04.2006
Апрель	12 апреля

Формулы

Понятие формулы

Назначение электронной таблицы в первую очередь состоит в автоматизации вычислений. Для этого в ячейки таблицы вводятся формулы.

Ввод любой формулы начинается со знака равенства. Если его пропустить, то вводимая формула будет воспринята как текст.

В формулы можно включать числовые данные, знаки операций, различные функции, а также адреса объектов таблицы. Формулу, в которой содержатся адреса ячеек, можно сравнить с записью уравнения в математике, где вместо адресов ячеек используются переменные.

Адреса, которые используются в формулах, получили название ссылок. Ссылки позволяют связывать между собой любые ячейки электронной таблицы и производить необходимую обработку табличных данных.

Ссылка — это адрес объекта (ячейки, строки, столбца, диапазона ячеек), используемый при записи формулы.

Формулы представляют собой соединенные знаками арифметических и логических операций операнды. Операндом может быть конкретное значение, ссылка или функция.

Различают арифметические (алгебраические) и логические формулы.

Арифметические формулы. Арифметические формулы аналогичны математическим соотношениям. В них используются арифметические операции (сложение « + », вычитание «-», умножение «*», деление «/», возведение в степень «˄»). При вычислении по формулам соблюдается принятый в математике порядок выполнения арифметических операций: сначала выполняется возведение в степень, затем — умножение и деление, после этого — сложение и вычитание. Операции одного уровня, такие как умножение и деление, выполняются слева направо.

Для изменения порядка выполнения арифметических операций используют круглые скобки. Действия над операндами, заключенными в круглые скобки, выполняются в первую очередь.

Результатом вычислений по арифметической формуле является число. При каждом изменении входящих в формулу операндов результат пересчитывается заново и отображается в соответствующей ячейке.

Пример вычисления по арифметическим формулам:

  Пусть в ячейке СЗ введена формула =А1+7*В2, а в ячейках А1 и В2 находятся числовые данные 3 и 5 (рис. 4.6, а). Тогда при вычислении по заданной формуле сначала будет выполнена операция умножения числа 7 на содержимое ячейки В2 (5) и к этому числу будет прибавлено содержимое ячейки А1 (3). Полученный результат, равный 38, будет отображен в ячейке СЗ, в которой находится формула (рис. 4.6, б).
  В данной формуле А1 и В2 представляют собой ссылки на ячейки. Смысл использования ссылок состоит в том, чтобы при изменении значений операндов автоматически изменялся результат вычислений, выводимый в ячейке СЗ. Например, пусть значение в ячейке А1 стало равным 1, а значение в ячейке В2 — 10. Тогда в ячейке СЗ появляется новое значение — 71 (рис. 4.6, в).

Рис. 4.6. К примеру вычислений по арифметическим формулам

Логические формулы. Логическая формула содержит условие и определяет, истинно оно или ложно. Истинному выражению присваивается значение «истина» (1), а ложному — «ложь» (0).

Однотипные формулы

При работе с электронной таблицей часто возникает необходимость в заполнении некоторого диапазона ячеек формулами, имеющими одинаковую структуру, но разные значения переменных. Это означает, что они различаются ссылками. Подобные формулы получили название однотипных.

Однотипные (подобные) формулы — это формулы, которые имеют одинаковую структуру (строение) и различаются только конкретными ссылками.

Для упрощения и ускорения ввода однотипных формул используется следующий прием. Формулу вводят только в одну (начальную) ячейку, после чего ее копируют в другие ячейки.

Пример однотипных формул:

Относительная, абсолютная и смешанная адресация

В однотипных формулах могут быть использованы самые разные ссылки. Возможны однотипные формулы, в которых часть ссылок при переходе от одной формулы к другой изменяются закономерным образом, а другие входящие в формулу ссылки остаются неизменными для всех формул.

При копировании формулы в другое место таблицы прежде всего необходимо определить способ автоматического изменения входящих в нее ссылок. Для этого используются относительные, абсолютные и смешанные ссылки.

♦ Относительная ссылка используется в формуле в том случае, если она должна изменяться при копировании.

Пример:

Относительная ссылка записывается в обычной форме, например F3, Е7. Во всех ячейках, куда она будет помещена после копирования, изменяется и буква столбца, и номер строки.

♦ Абсолютная ссылка используется в формуле в том случае, если при ее копировании не должны изменяться обе части: буква столбца и номер строки.

Пример:

В абсолютной ссылке перед буквой столбца и перед номером строки ставится символ $, например $F$3, $Е$7. При копировании во все ячейки формула будет помещена в неизменном виде. 

♦ Смешанная ссылка используется, когда при копировании формулы меняется только какая-то одна часть ссылки — либо буква столбца, либо номер строки. При этом символ $ ставится перед той частью ссылки, которая должна остаться неизменной.

Пример:

Смешанные ссылки с неизменяемой буквой столбца: $С8, $F12. Смешанные ссылки с неизменяемым номером строки: А$5, F$9.

Абсолютная ссылка — это ссылка, не изменяющаяся при копировании формулы.

Относительная ссылка — это ссылка, автоматически изменяющаяся при копировании формулы.

Смешанная ссылка — это ссылка, частично изменяющаяся при копировании.

Правило изменения относительных ссылок при копировании формул

Для правильного заполнения ячеек при копировании формул важно понимать правило относительной ориентации. Это правило объясняет, как изменяются входящие в скопированные формулы относительные или смешанные ссылки.

Правило относительной ориентации:
Относительные ссылки в формуле определяют взаимное расположение ячеек с исходными данными и ячейки, в которой хранится результат вычисления.

Поясним смысл этого правила. На рис. 4.7 показан пример записи в ячейку С2 формулы, содержащей относительные ссылки на данные, хранящиеся в ячейках А1 и В4. Эти относительные ссылки указывают на взаимное расположение в таблице ячеек с исходными данными — операндов А1 и В4 — и результата вычисления по формуле, записанной в С2. 

Правило относительной ориентации выполняется табличным процессором следующим образом:

♦ ссылка А1 указывает, что значение первого операнда берется из ячейки, расположенной на одну строку выше и на два столбца левее той, в которую будет помещена формула (здесь — С2);
♦ ссылка В4 указывает, что значение второго операнда берется из ячейки, смещенной на две строки вниз и на один столбец влево относительно места записи формулы (здесь — С2).

Правила копирования формул

1. Ввести формулу, указав в ней относительные и абсолютные ссылки. Такая формула представляет собой образец (шаблон), указывающий положение ячеек, в которых хранятся операнды, относительно положения ячейки с формулой.

2. После ввода исходной формулы необходимо скопировать ее в нужные ячейки. При копировании формул действует правило относительной ориентации ячеек, благодаря которому обеспечивается автоматическая настройка относительных ссылок во всех копиях формулы. Для запрета автоматического изменения ссылок при копировании следует использовать абсолютные ссылки в исходной формуле.

Порядок копирования формулы из ячейки в диапазон:

♦ выделите ячейку с исходной формулой;
♦ скопируйте формулу в буфер обмена;
♦ выделите диапазон ячеек, в который должна быть скопирована исходная формула;
♦ вставьте формулу из буфера, заполнив ею все ячейки выделенного диапазона.

Порядок копирования формул из одного диапазона в другой:

♦ выделите диапазон с формулами, которые должны быть скопированы;
♦ скопируйте формулы из выделенного диапазона в буфер обмена;
♦ установите курсор на первую ячейку диапазона, в который требуется скопировать формулы;
♦ вставьте формулы из буфера.

Пример копирования формул с использованием ссылок различных типов приведен на рис. 4.8:

а) с относительными ссылками;
б) с абсолютными ссылками;
в) со смешанными ссылками.

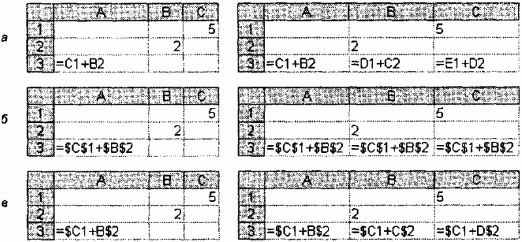
Рис. 4.8. Пример копирования формул с относительными (а), абсолютными (б) и смешанными ссылками(в)

Контрольные вопросы и задания

1. Перечислите объекты электронной таблицы.

2. Как задается адрес диапазона ячеек?

3. Перечислите параметры ячейки.

4. Из каких элементарных объектов состоит любая диаграмма?

5. Назовите основные типы диаграмм в табличном процессоре.

6. Назовите параметры, характеризующие любую диаграмму.

7. Назовите типы данных, используемых в табличном процессоре, и их особенности. Приведите примеры.

8. Что такое ссылка в электронной таблице и чем она отличается от адреса?

9. Что такое относительная адресация в формулах? Приведите примеры.

10. Что такое абсолютная адресация в формулах и как она обозначается? Приведите примеры.

11. Поясните на примере правило относительной ориентации.

12. Объясните на примерах правило автоматического изменения относительных ссылок при копировании.

13. Расскажите правила копирования формул.

14. Объясните на примерах результат копирования формулы, которая содержит:

а) константы и относительные ссылки;
б) относительные и абсолютные ссылки;
в) смешанные ссылки;
г) константы и все виды ссылок.