Урок 32
Логические основы построения компьютера

Изучив эту тему, вы узнаете:

- что изучает алгебра логики;
- какие операции возможны над высказываниями;
- как составляется таблица истинности;
- каким законам подчиняются логические выражения;
- что такое логические элементы компьютера.

Некоторые законы булевой алгебры

Существуют законы (аксиомы), позволяющие преобразовывать сложные логические выражения с целью их упрощения. Некоторые из них приведены в таблице 23.6.

Таблица 23.6. Основные законы булевой алгебры

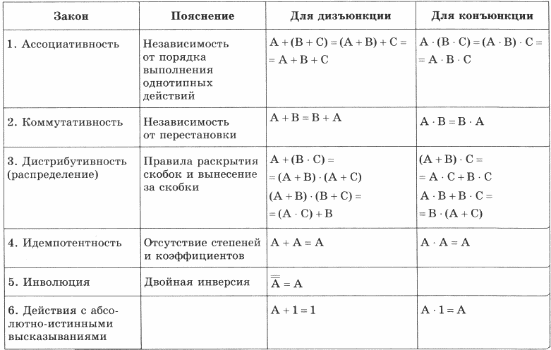
Таблица 23.6. Основные законы булевой алгебры (Продолжение)

Упрощение логического выражения состоит в преобразовании его к более простому (по числу исходных высказываний, операций), но равносильному выражению. Логические функции равносильны, если совпадают их таблицы истинности при всех одинаковых наборах значений.

Для проверки правильности приведенных в таблице 23.6 законов следует установить равносильность их левой и правой части на множестве значений всех переменных, входящих в данную формулу. Это можно сделать одним из следующих способов:

- воспользоваться простыми правилами-подсказками;
- сравнить таблицы истинности для правой и левой части равенства;
- привести правую часть равенства к левой части (или наоборот), применив уже известные или доказанные законы;
- привести обе части равенства к одному выражению.

Приведем примеры доказательств некоторых законов.

Пример 23.1

Для приведенного выше правила раскрытия скобок больше подойдет способ сравнения таблиц истинности (таблица 23.7).

Таблица 23.7. Доказательство при помощи сравнения таблиц истинности

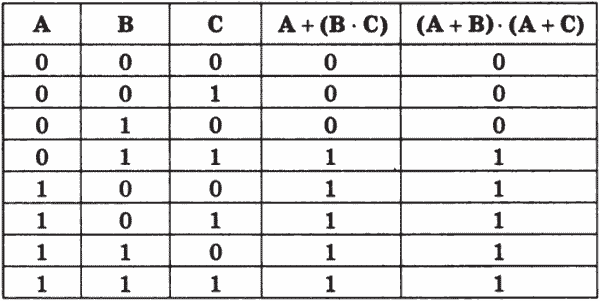
Таким же способом можно доказать законы де Моргана.

Пример 23.2

Для доказательства закона поглощения приведем левую часть к правой, используя уже проверенные нами законы: вы несение за скобки и сложение с абсолютно истинными высказываниями.

А + А • В = А • (1 + В) = А • 1 = А.

Пример 23.3

Для доказательства закона поглощения отрицания приведем левую часть к правой, используя следующие законы: раскрытие скобок для дизъюнкции, закон исключенного третьего и конъюнкцию с абсолютно истинным выражением.

А + 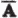• В = • В 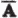+ А = ( + А) • (В + А) = 1 • (А + В) = А + В.

Доказательства остальных законов проведите самостоятельно.

Определение логического выражения по таблице истинности

Нахождение логической формулы

Условимся называть задачу построения таблицы истинности по формуле сложного высказывания — прямой задачей. Тогда обратная задача — построение логической формулы по таблице истинности. Полученную формулу будем записывать в виде логической функции.

Рассмотрим несколько примеров.

Пример 23.4

Приведена таблица истинности для аргументов А, В, по которой надо составить логическое выражение F(A,B).

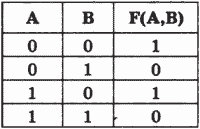
Алгоритм нахождения искомой формулы таков:

1. Выделить в таблице истинности строки, в которых выражение истинно (1);

2. Соединить операцией И (умножением) содержимое столбцов аргументов для выбранных строк. При этом если в таблице «О», пишем входной сигнал с отрицанием, а если в таблице «1», то без отрицания:

3. Соединить операцией ИЛИ полученные выражения.

F(A, В) = 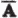• 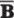+ А • .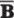

4. Это и есть искомая формула. Однако она громоздка и ее следует упростить. Получаем очень простой результат.

F(A,B) = 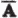• 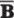+ А • = • ( +А) = .

Пример 23.5

Приведена таблица истинности для аргументов А, В, С, по которой надо составить логическое выражение F(A,B,C). Дополняем таблицу столбцами, названными «Отмечаем» и «Записываем». Выполняем действия в соответствии с алгоритмом, описанным в примере 23.1.

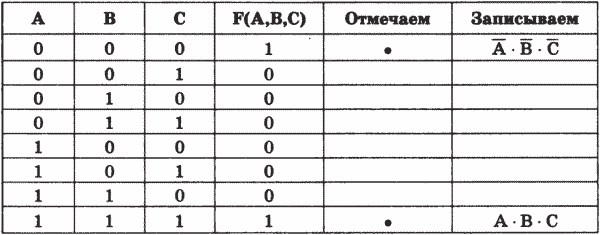
Соединим полученные формулы операцией ИЛИ и получим формулу:

F(A,B,C) = 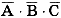+ А - В - С.

Пример 23.6

Приведена таблица истинности для аргументов А, В, по которой надо составить логическое выражение F(A,B). Дополняем таблицу столбцами, названными «Отмечаем» и «Записываем» и выполняем действия в соответствии с алгоритмом, описанным в примере 1.

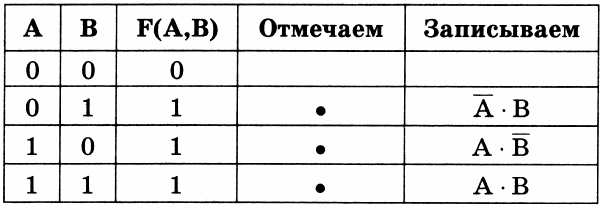
Получаем формулу:

F(A,B) = 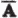• В + А • 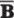+ А • В.

Внимательно посмотрите на таблицу истинности. Не соответствует ли она логической операции ИЛИ?

Если это так, то полученная формула должна быть эквивалентна формуле А + В.

Попробуем это доказать, пользуясь правилами преобразований, которые приведены выше.

Вынесем за скобки «общий множитель» В из 1-го и 3-го «слагаемых» нашего выражения, а 2-е оставим без изменения:

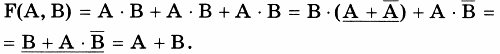
Подчеркнутые выражения упрощаем по правилам 9 и 10, приведенным в таблице 23.6.

Пример 23.7

Приведена таблица истинности для аргументов А, В, С, по которой надо составить логическое выражение F(A,B,C). 

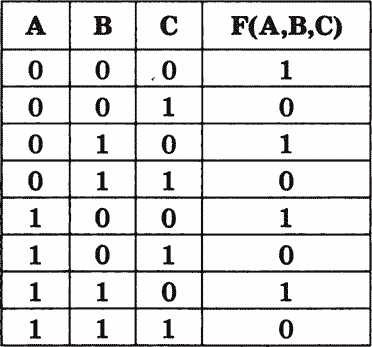
Если внимательно посмотреть на таблицу истинности, становится очевидным, что результат преобразования не зависит от А и В. Результирующий столбец является отрицанием содержимого столбца С. Попробуйте самостоятельно доказать, что громоздкое логическое выражение, которое можно получить по приведенному выше алгоритму, упрощается до 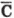, то есть F(A, В,С) = .

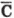Пример 23.8

Приведена таблица истинности для аргументов А, В, по которой надо составить логическое выражение F(A,B).

Очевидно, что результирующий столбец повторяет 1-й, то есть искомая формула упростится до F(A,B) = А.

На приведенных примерах вы убедились, что:

♦ алгоритм, по которому получается формула, верен;
♦ полученная формула часто требует упрощения (минимизации).

С какой целью следует упрощать полученную формулу?

Формула определяется для того, чтобы реализовать ее в физическом устройстве в виде электронной схемы. Упрощение формулы приводит к упрощению схемы, которая будет создана для ее реализации.

Логические элементы и основные логические устройства компьютера

Представление о логическом элементе

Любая информация при обработке на компьютере представляется в двоичной форме, то есть кодируется некоторой последовательностью, состоящей из 0 и 1. Упрощенно можно представить работу компьютера как некоторого устройства, производящего обработку двоичных сигналов, соответствующих 0 и 1. Такую обработку в компьютере выполняют логические элементы (вентили). Логический элемент — это электронное устройство, выполняющее одну из основных логических операций: И, ИЛИ, НЕ (рисунок 23.1). Условные обозначения логических элементов являются стандартными и используются при составлении логических схем компьютера.

Технически логический элемент реализуется в виде электрической схемы, которая представляет собой соединение различных деталей: диодов, транзисторов, резисторов, конденсаторов.

На вход логического элемента поступают электрические сигналы высокого и низкого уровней напряжения, которые интерпретируются в зависимости от реализуемых функций и на выход выдается один выходной сигнал также либо высокого, либо низкого уровня. Эти уровни соответствуют одному из состояний двоичной системы: 1 — 0; ИСТИНА — ЛОЖЬ.

Рис. 23.1. Логические элементы НЕ, ИЛИ, И

Из логических элементов составляются электронные логические схемы, выполняющие более сложные логические операции. Компьютер конструируют из отдельных электронных схем.

Тысячи микроскопических электронных переключателей в кристалле интегральной схемы сгруппированы в системы, выполняющие логические и арифметические операции над двоичными числами. Соединенные в различные комбинации, логические элементы дают возможность компьютеру решать сложнейшие задачи с помощью закодированных импульсов его двоичного языка.

Проектирование логических схем

Научившись составлять и упрощать логическую формулу по заданной таблице истинности, можно приступить к составление схем из логических элементов. Покажем на примере всю цепочку действий от исходной таблицы истинности до логической схемы.

Предположим, что нам надо создать электронное устройство, у которого на выходе будет сигнал тогда, когда входные сигналы не совпадают. Исходная таблица истинности будет иметь такой вид:

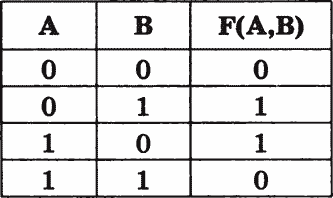
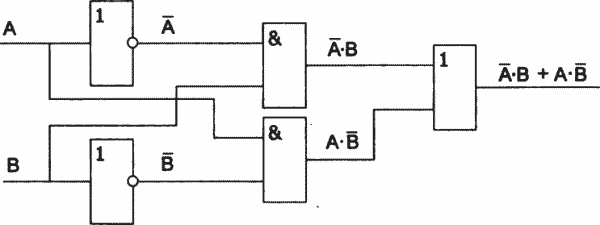
Рис. 23.2. Логическая схема по неупрощенной формуле

По таблице истинности можно получить логическую формулу:

F(A,B) = 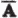• В + А • .

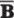В полученной формуле 5 операций: 2 — операции отрицания, 2 — конъюнкции и 1 — дизъюнкции.

Логическая схема будет иметь вид, представленный на рисунке 23.2. 

Схема получилась достаточно сложной, так как полученная по таблице истинности формула не была минимизирована. Применив к формуле законы логики (таблица 23.6), ее можно упростить:

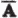• В + А • 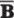= 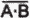• (А + В).

Докажите эквивалентность этих формул самостоятельно.

В упрощенной формуле 4 операции: 1 операция отрицания, 2 — конъюнкции и 1 — дизъюнкции.

Логическая схема для упрощенной формулы будет иметь вид, представленный на рисунке 23.3.

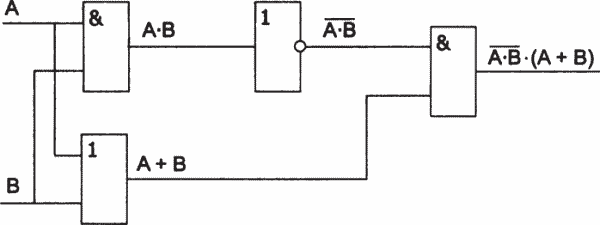
Рис. 23.3. Логическая схема по минимизированной формуле

Примером проектирования логической схемы может служить построение полусумматора для сложения двух двоичных цифр. Если учесть, что все математические операции, осуществляемые компьютером — умножение, деление, возведение в степень, вычисление интегралов, решение дифференциальных уравнений и т. д., — в конечном счете, сводятся к выполнению по определенным правилам операций сложения, то станет ясно, что сумматор — один из важных узлов ЭВМ.

Полусумматор — схема соединения логических элементов, которая обеспечивает сложение двух бит. На вход полусумматора поступает два сигнала, каждый из которых может быть равен О или 1. На выходе также два сигнала — один является двоичной суммой входных сигналов, другой — значение разряда переноса в старший разряд. 

Схема полусумматора не имеет третьего входа, на который мог бы поступать бит переноса от предыдущего разряда суммы. Поэтому обычно полусумматор реализует сложение только младших разрядов двоичных слагаемых.

Итак, изобразим таблицу истинности полусумматора:

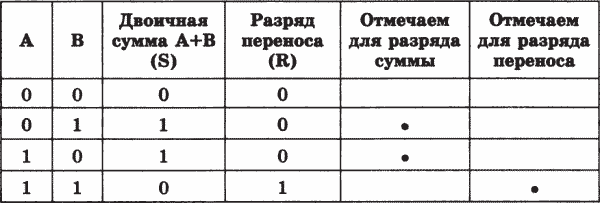
По таблице истинности составим формулы для разряда суммы и разряда переноса:

S = (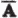• В) + (А • В);

R = А • В.

Для разряда сложения (по формуле S) нами уже составлена логическая схема в предыдущем примере. Значение для разряда переноса (по формуле R) можно взять как промежуточное значение из той же схемы.

В более компактном виде схема полусумматора представлена на рис. 23.4.

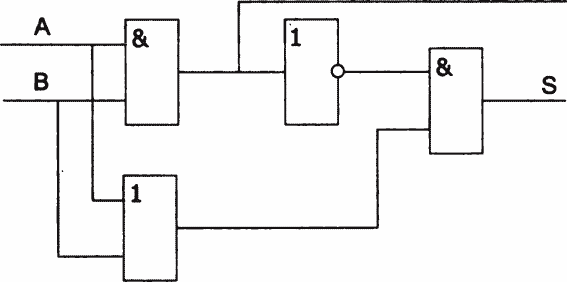
Рис. 23.4. Схема полусумматора

Контрольные вопросы и задания

1. Что изучает алгебра логики?

2. Приведите примеры простых высказываний.

3. Являются ли следующие предложения высказываниями:

■ если D < 0, то уравнение не имеет решения;
■ алгоритм — последовательность действий (план);
■ в гелиоцентрической системе все планеты вращаются вокруг Земли.

4. Приведите примеры сложных высказываний.

5. Сколько строк будет в таблицах истинности для сложных высказываний:

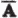■ + В;
■ (А + В) • .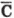

6. Постройте таблицу истинности для сложного высказывания

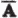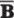■ ( + ) • C .

7. Упростите следующие логические выражения:

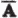■ ( + В) • ;
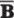■ А + 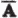• В + С • В;
■ (А + В) • (А + 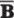) • С.

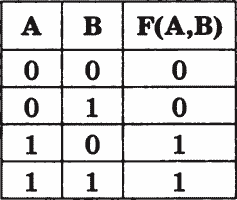
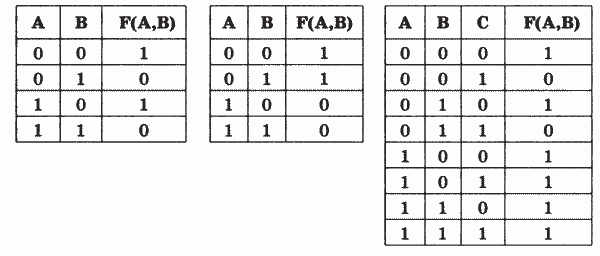
8. По заданным таблицам истинности найдите логические выражения и упростите их:

9. Постройте логические схемы по заданным логическим выражениям:

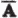■ ( + В) • С;
■ + + ;
■ .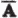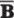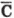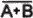