Урок 7
§11. Логические выражения
Содержание урока
Составление условий
Составление условий
Логические выражения часто используются при решении математических задач с помощью компьютеров.
Построим условия (логические выражения), соответствующие заштрихованным областям на числовой оси (рис. 2.22).

Рис. 2.22
На рисунке 2.22, а выделен отрезок [3; 6]. Для того чтобы определить такую область, нужно ограничить значение х с двух сторон: оно должно быть больше или равно трём и меньше или равно шести, причем эти два условия должны выполняться одновременно, т. е. их нужно связать с помощью операции И:
(3 ≤ х) и (х ≤ 6).
Область на рис. 2.22, б — это объединение двух отрезков. Мы можем отдельно записать условия для каждого отрезка и связать их с помощью операции ИЛИ:
(1 ≤ х) и (х ≤ 3) или (5 ≤ х) и (х ≤ 8).
Запишите условие, которое определяет область на рис. 2.22, в.
Теперь рассмотрим задачу с областью на плоскости. Запишем условие, соответствующее заштрихованной части (рис. 2.23).
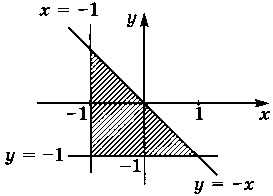
Рис. 2.23
Требуется составить логическое выражение, зависящее от переменных х и у, которое будет равно 1 (истинно) внутри заштрихованной области и равно 0 вне её.
Выделенная область находится справа от вертикальной линии х = -1, поэтому должно выполняться условие х ≥ -1, которое определяет полуплоскость (рис. 2.24).
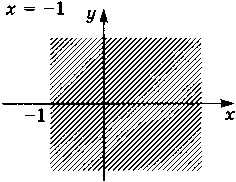
Рис. 2.24
Кроме того, все точки области находятся выше горизонтальной линии у = -1 и ниже наклонной прямой у = —х, что даёт ещё два условия: у ≥ -1 и у ≤ -х. Все три простых условия должны выполняться одновременно, поэтому их нужно связать с помощью двух операций И:
(х ≥ -1) и (у ≥ -1) и (у ≤ -х).
Запишите условие, которое определяет области на рисунках (рис. 2.25).
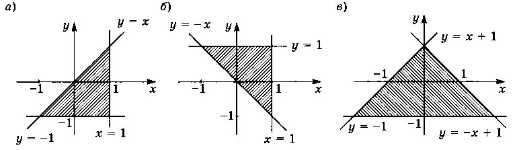
Рис. 2.25
Построим логическое выражение для области на рис. 2.26.
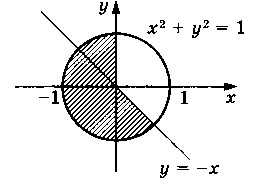
Рис. 2.26
Можно разделить заштрихованную область на две части (рис. 2.27).
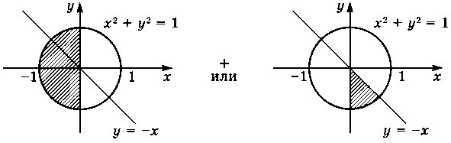
Рис. 2.27
Обе области находятся внутри круга радиуса 1 с центром в начале координат, т. е. в области х2 + у2 ≤ 1. Первая область описывается выражением(х2 + у2 ≤ 1) и (х ≤ 0),
а вторая — выражением
(х2 + у2 ≤ 1) и (х ≥ 0) и (у ≤ -х).
Поскольку нам нужно «сложить» две области, эти выражения нужно объединить с помощью операции логического сложения (ИЛИ):
(х2 + у2 ≤ 1) и (х ≤ 0) или (х2 + у2 ≤ 1) и (х ≥ 0) и (у ≤ -х).
Общее условие х2 + у2 ≤ 1 можно вынести за скобки:
(х2 + у2 ≤ 1) и ((х ≤ 0) или (х ≥ 0) и (у ≤ -х)).
Попробуйте ещё упростить полученное условие.
Запишите условие, которое определяет области на рисунках (рис. 2.28).
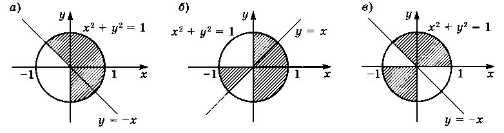
Рис. 2.28
Следующая страница  Логические схемы
Логические схемы

