Урок 11
§15. Табличные модели. Диаграммы
Содержание урока
Оптимальный маршрут
Оптимальный маршрут
Рассмотрим задачу, которая требует анализа табличных данных: определение оптимального (самого лучшего) маршрута поездки.
 Задача. Путешественник прибыл в посёлок Берёзовое в 8 утра по местному времени и увидел следующее расписание автобусов (табл. 3.4).
Задача. Путешественник прибыл в посёлок Берёзовое в 8 утра по местному времени и увидел следующее расписание автобусов (табл. 3.4).
Таблица 3.4
| Отправление из | Прибытие в | Время отправления | Время прибытия |
| Берёзовое | Лесное | 07:30 | 10:00 |
| Берёзовое | Осиновое | 11:50 | 14:10 |
| Лесное | Берёзовое | 12:50 | 15:20 |
| Полевое | Лесное | 13:20 | 14:40 |
| Осиновое | Полевое | 14:00 | 17:15 |
| Лесное | Осиновое | 14:20 | 15:30 |
| Осиновое | Лесное | 14:40 | 15:50 |
| Берёзовое | Полевое | 16:00 | 17:50 |
| Лесное | Полевое | 16:10 | 17:30 |
| Полевое | Осиновое | 17:40 | 19:55 |
Определите самое раннее время, когда он может попасть в посёлок Полевое, и как ему нужно ехать.
Из расписания видно, что автобусы ходят между четырьмя населёнными пунктами. Нарисуем схему, показывающую все возможные способы переезда из посёлка Березовое в посёлок Полевое. Буквы в кружках обозначают посёлки (Б — Берёзовое, П — Полевое, Л — Лесное и О — Осиновое), а слева и справа от них записано время отправления и прибытия автобусов согласно расписанию (рис. 3.3).
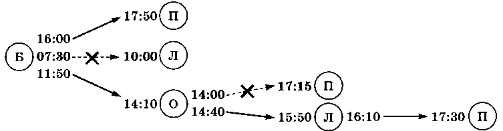
Рис. 3.3
Сравните таблицу 3.1 и схему на рис. 3.3. Ответьте на вопросы.
— Что означают буквы Б, П, Л и О в кружках?
— Что обозначают числа справа и слева от кружков?
— Что обозначают штриховые линии, перечёркнутые крестиками?
— Какие варианты маршрута есть у путешественника? Сколько их?
— Какой из этих вариантов позволяет быстрее добраться до Полевого?
Обратите внимание, что при поиске оптимального решения мы построили графическую модель задачи в виде дерева — многоуровневой структуры. С деревьями вы знакомы из курса 7 класса, скоро мы снова с ними встретимся.
Следующая страница  Анализ диаграмм
Анализ диаграмм

