Урок 15
Использование графов
§ 18. Игровые стратегии
Содержание урока
Выигрышные и проигрышные позиции
Выигрышные и проигрышные позиции
Ключевые слова:
• стратегия • выигрышная позиция • проигрышная позиция • дерево игры • неполное дерево игры
Как вы уже знаете из § 16, игровые модели — это модели, которые описывают соперничество двух (или более) сторон, каждая из которых стремится к выигрышу, т. е. преследует свою цель. Часто цели участников противоречивы — выигрыш одного означает проигрыш других.
Построением и изучением игровых моделей занимается теория игр — раздел прикладной математики. Задача состоит в том, чтобы найти стратегию (алгоритм игры), который позволит тому или другому участнику получить наибольший выигрыш (или, по крайней мере, наименьший проигрыш) в предположении, что соперники играют безошибочно.
 Стратегия — это алгоритм игры, который позволяет добиться цели в игре в предположении, что соперники играют безошибочно.
Стратегия — это алгоритм игры, который позволяет добиться цели в игре в предположении, что соперники играют безошибочно.
Мы будем изучать игры с полной информацией, в которых результат не зависит от случая (говорят, что в таких играх нет неопределённое™). Игроки делают ходы по очереди, в любой момент им известна позиция и все возможные дальнейшие ходы.
Можно ли считать играми с полной информацией «крестики-нолики», карточные игры, шахматы, шашки, «морской бой»?
Теоретически в играх с полной информацией можно построить последовательность ходов из заданной начальной позиции, которая приведёт одного из игроков к выигрышу или, по крайней мере, к ничьей. Нас будут интересовать простые игры, где не так много вариантов развития событий и перебор ходов возможен за приемлемое время. В большинстве игр, например в шахматах, количество вариантов настолько велико, что их полный перебор требует огромного времени и поэтому нереален.
Подсчитайте, сколько различных ходов могут сделать крестики в начале игры «крестики-нолики» на поле 3x3. Сколько различных позиций может возникнуть после ответного хода ноликов? После второго хода крестиков? После второго хода ноликов? Как можно сократить количество рассматриваемых вариантов в этой игре?
Подсчитайте, сколько различных ходов могут сделать белые в начале шахматной игры.
Все позиции (игровые ситуации) делятся на выигрышные и проигрышные.
 Выигрышная позиция — это такая позиция, в которой игрок, делающий первый ход, может гарантированно выиграть при любой игре соперника, если не сделает ошибку.
Выигрышная позиция — это такая позиция, в которой игрок, делающий первый ход, может гарантированно выиграть при любой игре соперника, если не сделает ошибку.
При этом говорят, что у него есть выигрышная стратегия — алгоритм выбора очередного хода, позволяющий ему выиграть.
 Проигрышная позиция — это такая позиция, в которой игрок, делающий первый ход, обязательно проиграет, если его соперник не сделает ошибку.
Проигрышная позиция — это такая позиция, в которой игрок, делающий первый ход, обязательно проиграет, если его соперник не сделает ошибку.
В этом случае говорят, что у него нет выигрышной стратегии. Таким образом, общая стратегия игры состоит в том, чтобы своим ходом создать проигрышную позицию для соперника.
Найдите среди позиций игры в «крестики-нолики», показанных на рис. 3.37, выигрышные и проигрышные. Во всех случаях ходят нолики.
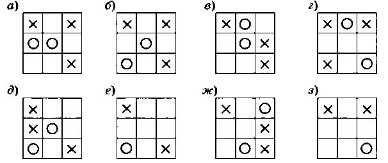
Рис. 3.37
Найдите все возможные ходы белых и чёрных фигур в позиции, показанной на рис. 3.38.

Рис. 3.38
Найдите выигрышный ход белых (они начинают).
Выигрышные и проигрышные позиции можно охарактеризовать так:
• позиция, из которой все возможные ходы ведут в выигрышные позиции, — проигрышная;
• позиция, из которой хотя бы один из возможных ходов ведёт в проигрышную позицию, — выигрышная, при этом выигрышная стратегия игрока состоит в том, чтобы перевести игру в эту проигрышную (для соперника) позицию.
В позициях, показанных на рис. 3.39, найдите выигрышный ход ноликов, который создаёт проигрышную (для крестиков) позицию.
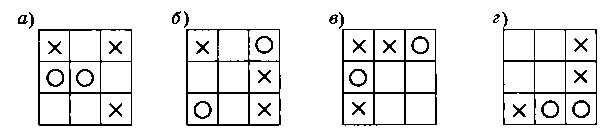
Рис. 3.39
Докажите, что все позиции, показанные на рис. 3.40, проигрышные для ноликов. Рассмотрите все возможные ходы и для каждого из них укажите выигрывающий ход крестиков.
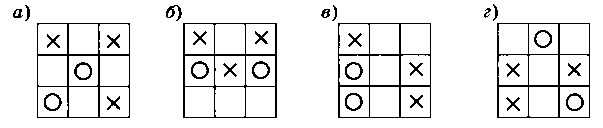
Рис. 3.40
Следующая страница  Дерево перебора вариантов
Дерево перебора вариантов

