Урок 29
Использование графов
§ 18. Игровые стратегии

Содержание урока

Выигрышные и проигрышные позиции

Дерево перебора вариантов

Решение без дерева

Исследование игры

Выводы

Вопросы и задания

Дерево перебора вариантов

Одна из простых игр, где можно перебрать все варианты, — это игра с камнями. Перед двумя игроками лежит куча из некоторого количества камней (обозначим его S) или других одинаковых предметов (монет, бусин, пуговиц и т. п.) За один ход игрок может взять один или два камня. Тот, кто возьмёт последний камень, проигрывает.

Сыграйте в эту игру с соседом несколько раз для S = 6. Начинайте игру по очереди.

Для небольших значений S легко построить дерево перебора вариантов. Для S = 4 такое дерево показано на рис. 3.41.

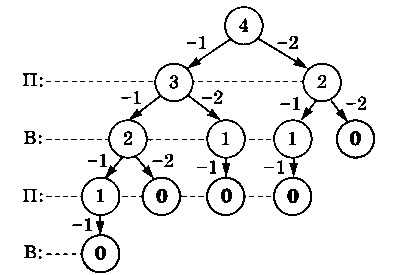
Рис. 3.41

Буквой П обозначены ходы первого игрока (пусть его зовут Петя), а буквой В — ходы второго игрока (будем называть его Ваней). Числа в узлах дерева показывают количество камней в куче после очередного хода, а «-1» и «-2» — взятие из кучи соответственно одного или двух камней.

Очевидно, что позиция S = 1 — проигрышная: тот, кто ходит в этой позиции, проигрывает, потому что берёт последний (единственный) камень. Тогда выигрышными будут все позиции, из которых можно получить S = 1 каким-либо ходом — это позиции S = 2 и S = 3.

Из позиции S = 4 все возможные ходы ведут в выигрышные позиции S = 2 и S = 3, поэтому эта позиция проигрышная. Если Ваня не сделает ошибку, то Петя в любом случае проиграет.

Используя дерево перебора вариантов, выясните, какой ход должен сделать Ваня, чтобы выиграть в позиции S = 2? В позиции S = 3?

Выигрышную стратегию можно показать с помощью неполного дерева игры. Дело в том, что для выигрывающего игрока нам достаточно указать на каждом ходу один-единственный вариант, переводящий игру в проигрышную (для его соперника) позицию. А вот для проигрывающего игрока на каждом ходу нужно рассматривать все варианты, чтобы доказать, что он никак не может избежать поражения. Построим неполное дерево для начальной позиции S = 4, в которой, как мы показали, выигрышная стратегия есть у второго игрока (рис. 3.42).

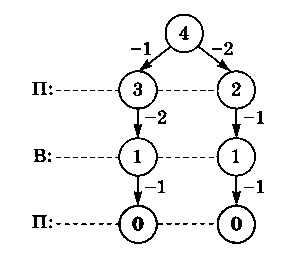
Рис. 3.42

По этому дереву видно, что при любом своём первом ходе Петя обязательно проигрывает на втором ходу, взяв последний камень (если, конечно, Ваня не ошибётся).

Постройте дерево перебора вариантов для игры с камнями при S = 6. Выясните, какова начальная позиция — выигрышная или проигрышная. Почему? Постройте неполное дерево игры с доказательством стратегии выигрывающего игрока.

По результатам исследований определите, при каких значениях S начальные позиции будут выигрышными, а при каких — проигрышными. Если позиция выигрышная, какой стратегии должен следовать Петя?

Следующая страница Решение без дерева

Cкачать материалы урока