Урок 35
Построение и исследование физических моделей
§ 2.4. Построение и исследование физических моделей
Содержание урока
2.4. Построение и исследование физических моделей
2.4. Построение и исследование физических моделей
Рассмотрим процесс построения и исследования модели на конкретном примере движения тела, брошенного под углом к горизонту.
Содержательная постановка задачи «Бросание мячика в площадку». В процессе тренировок теннисистов используются автоматы по бросанию мячика в определенное место площадки. Требуется задать автомату необходимую скорость и угол бросания мячика для попадания в площадку определенной длины, находящуюся на известном расстоянии (рис. 2.15).
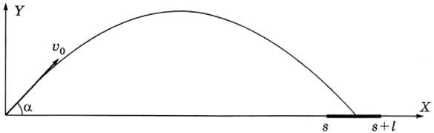
Рис. 2.15. Бросание мячика в площадку
Качественная описательная модель. Сначала построим качественную описательную модель процесса движения тела с использованием физических объектов, понятий и законов, т. е. в данном случае идеализированную модель движения объекта. Из условия задачи можно сформулировать следующие основные предположения:
• мячик мал по сравнению с Землей, поэтому его можно считать материальной точкой;
• изменение высоты мячика мало, поэтому ускорение свободного падения можно считать постоянной величиной g = 9,8 м/с2 и движение по оси Y можно считать равноускоренным;
• скорость бросания тела мала, поэтому сопротивлением воздуха можно пренебречь и движение по оси X можно считать равномерным.
Формальная модель. Для формализации модели используем известные из курса физики формулы равномерного и равноускоренного движения. При заданных начальной скорости и0 и угле бросания а значения координат дальности полета х и высоты у от времени можно описать следующими формулами:
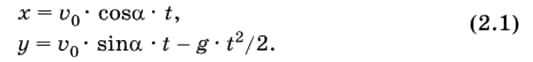
Площадка расположена на поверхности Земли, поэтому из второй формулы (2.1) можно выразить время, которое понадобится мячику, чтобы достичь площадки:
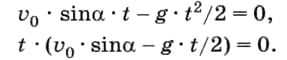
Значение времени t = 0 не имеет физического смысла, поэтому:
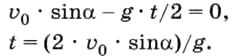
Подставим полученное выражение для времени в формулу для вычисления координаты х:
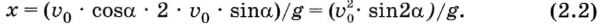
Формализуем теперь условие попадание мячика в площадку. Пусть площадка расположена на расстоянии s и имеет длину l (см. рис. 2.16). Тогда попадание произойдет, если значение координаты х мячика будет удовлетворять условию в форме неравенства:
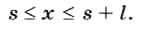
Если х < s, то это означает «недолет», а если х > s + l, то это означает «перелет».
Компьютерная модель движения тела. На основе формальной модели, описывающей движение тела, брошенного под углом к горизонту, можно создать компьютерную модель с использованием системы программирования, например системы объектно-ориентированного программирования Visual Basic, так как она позволяет визуализировать траектории движения тела.
На основе данной формальной модели можно создать компьютерную модель также с использованием электронных таблиц Microsoft Excel или OpenOffice.org Calc. Траектория движения тела визуализируется с использованием диаграммы типа График.
Контрольные вопросы
1. Какие основные предположения можно сделать при построении качественной описательной модели бросания мячика под углом к горизонту? 2. Чем отличается компьютерная модель от формальной модели?
Cкачать материалы урока
