Урок 5
Представление числовой информации в компьютере

Перевод чисел из недесятичной позиционной системы счисления в десятичную

Изучив эту тему, вы узнаете и повторите:

- какие системы счисления существуют;
- как осуществляется перевод чисел из одной системы счисления в другую;
- с какими системами счисления работает компьютер;
- как представляются различные числа в памяти компьютера.

Познакомимся с общими правилами перевода чисел из одной позиционной системы счисления в другую на нескольких примерах.

Представим двоичное число 10110,1012 в виде суммы слагаемых, а затем произведем их сложение:

10110,101₂ = 1*2⁴ + 0*2³ + 1*2² + 1*2¹ + 0*2⁰ + 1*2^-1 + 0*2^-2 + + 1*2^-3 = 16+0+4+2+0+0,5+0+0,125 =22,625₁₀

Таким образом, 10110,101₂ = 22,625₁₀

Представим шестнадцатеричное число 5D8,AC1₁₆ в виде суммы слагаемых, а затем произведем их сложение:

5D8,AC1₁₆ = 5*16² + 13*16¹ + 8*16⁰ + 10*16^-1 + 12*16^-2 + + 1*16^-3 = 1280 + 208 + 8 + 0,625 + 0,047 + 0,006 = 1496,678₁₀

Таким образом, 5D8,AC1₁₆ = 1496,678₁₀

Перевод числа из десятичной системы счисления в другую позиционную систему

Представим десятичное число в общем виде N,M, где N — целая часть числа, а М — его дробная часть. Для перевода десятичного числа в позиционную систему счисления с основанием р необходимо воспользоваться двумя правилами: одно определяет технологию перевода целой части числа, а другое — дробной части.

Правило перевода целой части числа состоит из следующих этапов:

♦ число N делится на новое основание р;
♦ полученный остаток запоминается или записывается (это будет цифра младшего разряда);
♦ целая часть полученного частного снова делится на р;
♦ опять запоминаем полученный остаток (это будет цифра следующего разряда) и т. д.

Такое последовательное деление продолжается до тех пор, пока целая часть частного не окажется меньше, чем основание системы счисления р. Эта последняя целая часть частного будет цифрой старшего разряда. Результат формируется путем последовательной записи слева направо цифры старшего разряда и всех записанных остатков в порядке, обратном их получению.

Правило перевода дробной части числа состоит из следующих этапов:

♦ дробная часть числа умножается на основание р\
♦ запоминается или записывается цифра результата, переносимая в целую часть;
♦ оставшаяся дробная часть числа умножается на основание р;
♦ снова фиксируется цифра результата, переносимая в целую часть, и т. д.

Такое последовательное умножение продолжается до тех пор, пока в дробной части не будет получен ноль или достигнута требуемая точность, например 5 знаков после запятой. Результат формируется в виде последовательной записи зафиксированных цифр переносов в целую часть в том порядке, в котором они были получены.

Рассмотрим примеры.

Требуется перевести десятичные числа 13,126 и 10,8 в двоичную систему счисления. Технология перевода в соответствии с приведенными правилами отражена в табл. 1.4.

Таблица 1.4. Пример перевода из десятичной системы счисления в двоичную

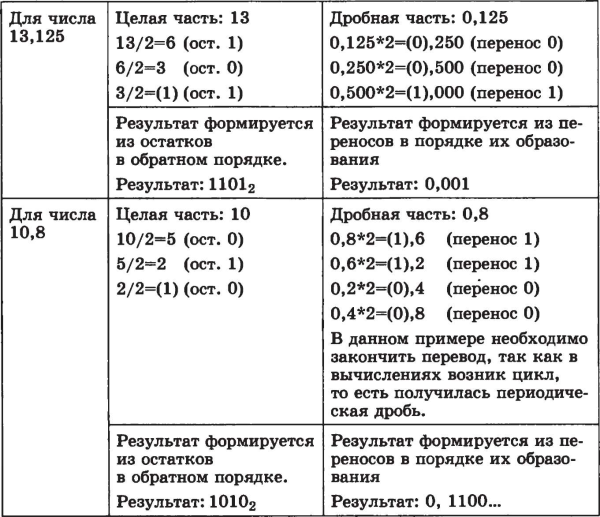
Общий результат перевода: 13,125₁₀=1101,001₂

10,8₁₀=1010,(1100)₂, где в скобках указан период дроби.