Урок 6
Представление числовой информации в компьютере

Соотношение систем счисления

Изучив эту тему, вы узнаете и повторите:

- какие системы счисления существуют;
- как осуществляется перевод чисел из одной системы счисления в другую;
- с какими системами счисления работает компьютер;
- как представляются различные числа в памяти компьютера.

Наряду с двоичной системой счисления в компьютере используются еще две — восьмеричная и шестнадцатеричная. Восьмеричную и шестнадцатеричную системы называют родственными двоичной, поскольку их основания являются степенями числа 2. Родственными, к примеру, являются системы с основаниями 3 и 9.

Перевод чисел внутри родственных систем (в частности, с основаниями 2, 8 и 16) упрощен, поскольку все цифры алфавита для систем с большим основанием можно представить совокупностью цифр системы с наименьшим основанием. Убедимся в этом, рассмотрев табл. 1.5. В ней приведено соотношение чисел в системах счисления с основаниями 10, 2, 8 и 16.

Таблица 1.5. Соотношение двоичной, восьмеричной, шесгнадцатеричной систем счисления

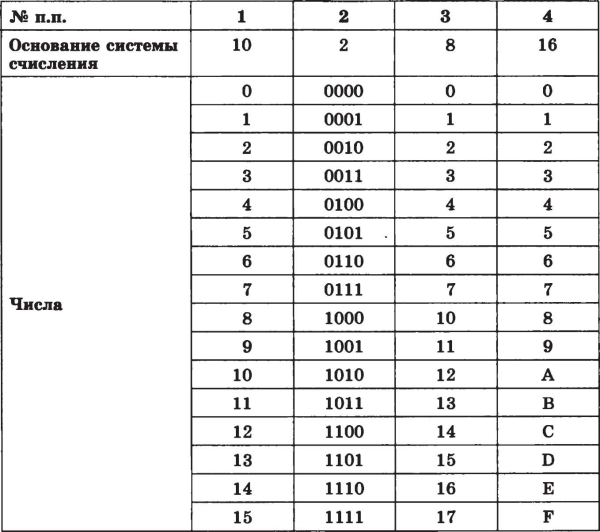
Если внимательно посмотреть на столбцы 2 и 3 табл. 1.5, то видно, что все восьмеричные цифры (от 0 до 7) можно записать при помощи трех двоичных разрядов. На этом основан быстрый перевод из восьмеричной системы в двоичную и наоборот.

Для перевода восьмеричного числа в двоичное достаточно каждую цифру этого числа заменить двоичной триадой (три разряда) в соответствии с таблицей. Например:

734,46₈=111 011 100,100 110₂.

Для перевода двоичного числа в восьмеричное следует воспользоваться следующим алгоритмом:

♦ разделить целую часть числа на триады от младших разрядов к старшим (влево от запятой);
♦ разделить дробную часть на триады в обратном направлении (вправо от запятой);
♦ заменить каждую триаду двоичных чисел соответствующей восьмеричной цифрой по табл. 1.5;
♦ недостающие до триады позиции заполнить незначащими нулями.

Например:

1010,11111₂ = 001 010,111 110₂ = 12,76₈

Подобным свойством обладают и шестнадцатеричные цифры. Все шестнадцатеричные цифры (от 0 до F) можно записать при помощи четырех двоичных разрядов (тетрады) (см. столбцы 2 и 4 табл. 1.5).

Взаимный перевод из шестнадцатеричной в двоичную систему и наоборот осуществляется аналогично, с той лишь разницей, что шестнадцатеричная цифра соответствует четырем двоичным разрядам. Например:

18AE,37F₁₆ - 0001 1000 1010 1110,0011 0111 1111₂

11010101110,00101111₂ - 0110 1010 1110,0010 1111₂ = 6AE,2F₁₆.