Урок 17
Информационные процессы в компьютере
Содержание урока
Однопроцессорная архитектура ЭВМ
Использование периферийных процессоров
Архитектура персонального компьютера
Архитектура ненеймановских вычислительных систем
Варианты реализации ненеймановских вычислительных систем
Архитектура ненеймановских вычислительных систем
Несмотря на стремительно нарастающую производительность ЭВМ, которая каждые 4 5 лет по важнейшим показателям практически удваивается, всегда есть классы задач, для которых никакой производительности не хватает. Укажем некоторые из них.
1. Математические расчеты, лежащие в основе реализации математических моделей многих процессов. Гигантские вычислительные ресурсы, которые можно реализовать очень быстро (как иногда говорят, в реальном масштабе времени), необходимы для более надежного и долгосрочного прогноза погоды, для решения аэрокосмических задач, в том числе и оборонных, для решения многих инженерных задач и т. д.
2. Поиск информации в гигантских базах данных, в информационном пространстве Интернета.
3. Моделирование интеллекта — при всех фантастических показателях, объем оперативной памяти современных компьютеров составляет лишь малую долю объема памяти человека.
Быстродействие компьютера с одним центральным процессором имеет физическое ограничение: повышение тактовой частоты процессора ведет к повышению тепловыделения, которое не может быть неограниченным. Перспективный путь повышения производительности компьютера лежит на пути отказа от единственности главных устройств компьютера: либо процессора, либо оперативной памяти, либо шины, либо всего этого вместе. Это путь еще большего отступления от архитектуры фон Неймана.
Чтобы стало понятнее, зачем компьютеру несколько процессоров, обсудим алгоритм решения простейшей математической задачи. Есть массив из 100 чисел: a1, а2, ... , а100. Требуется найти их сумму.
Нет ничего проще! И на компьютере, и без него мы, скорее всего, поступим так: сложим первые два числа, как-то обозначим их сумму (например, S), затем прибавим к ней третье, и будем делать это еще 98 раз. Это пример последовательного вычислительного процесса. Его блок-схема приведена на рис. 2.8.
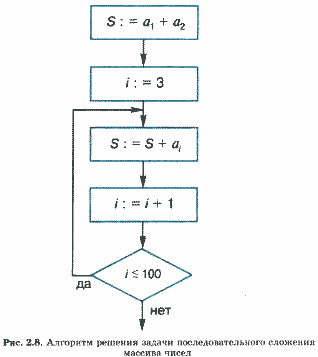
Поскольку у человека нет второй головы, иначе эту задачу в одиночку не решить. Но представим, что мы решаем ее не в одиночку, а всем классом (25 человек). Тогда возникает возможность совсем иной последовательности действий.
1. Объединим числа в пары — по два на каждого (итого распределили 50 чисел); например, ученик № 1 берет себе а1 и а2, ученик № 2 — а3 и а4, и т. д.
2. Даем команду «складывай!» — и каждый складывает свои числа.
3. Даем команду «записывай!» — и каждый записывает мелом на классной доске свой результат.
4. Поскольку у нас осталось еще 50 необработанных чисел (а51, ..., а100), повторяем пункты 1 - 3. После этого имеем на доске 50 чисел b1 = а1 + а2, ..., b50 = а99 + а100 — результаты парных сложений.
5. Объединим в пары числа bi и повторим выполнение пунктов 2 - 4.
Продолжаем этот процесс (2 - 5) до тех пор, пока не останется одно число — искомая сумма.
Первое впечатление, что очень сложно, гораздо сложнее, чем алгоритм на рис. 2.8. Если бы мы захотели записать этот алгоритм в виде блок-схемы, то нам бы пришлось кроме описания порядка и объектов действий сделать то, что мы никогда при записи алгоритмов не делали, — предусмотреть синхронизацию параллельных процессов по времени. Например, выполнение команд 2 и 3 должно завершиться всеми участниками вычислений до того, как они будут продолжены (до перехода к п. 4), иначе даже при решении этой простой задачи наступит хаос.
Но сложность не есть объективная причина отвергнуть такой путь, особенно если речь идет о возможности значительного ускорения компьютерных вычислений. То, что мы предложили выше, называется на языке программистов распараллеливанием вычислений и вполне поддается формальному описанию. Эффект ускорения вычислений очевиден: пункт 2 в приведенном выше алгоритме ускоряет соответствующий этап работы в 25 раз!
Следующий вопрос: что надо изменить в устройстве компьютера, чтобы он смог так работать? Для реализации подобной схемы вычислений компьютеру потребуется 25 процессоров, объединенных в одну архитектуру и способных работать параллельно.
Такие многопроцессорные вычислительные комплексы — реальность сегодняшней вычислительной техники.
Вернемся, однако, к описанной выше последовательности действий — в ней еще есть источники проблем. Представим себе, что в схеме на рис. 2.7 мы дорисовали еще 24 центральных процессора, соединенных с шиной. При реализации в таком компьютере команды 3 произойдет одновременное обращение 25 процессоров к системной шине для пересылки результатов сложения в оперативную память. Но поскольку шина одна, числа по ней могут пересылаться только по одному! Значит, для выполнения команды 3 придется организовать очередь на передачу чисел в память. Тут же возникает вопрос: не сведет ли к нулю эта очередь все преимущества от параллельности выполнения операций на шаге 2? А если преимущества останутся, то насколько они велики? Окупятся ли расходы на 24 дополнительных процессора?
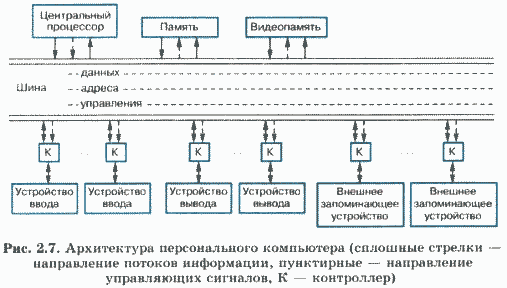
В возникшей ситуации естественен следующий шаг «изобретательской мысли»: ввод в архитектуру нескольких системных шин. А если еще подумать над возможными проблемами, то и нескольких устройств оперативной памяти.
Как видите, все это очень непросто! Обсуждаемые изменения в устройстве компьютера приводят к «ненеймановским» архитектурам. Изобретателям таких систем приходится искать компромисс между возрастающей сложностью (и, как следствие, — стоимостью) и ускорением их работы.
Следующая страница  Варианты реализации ненеймановских вычислительных систем
Варианты реализации ненеймановских вычислительных систем

