Уроки 28 - 29
Подпрограммы
Практикум
Практическая работа № 3.5
"Программирование с использованием подпрограмм"

Содержание урока

Вспомогательные алгоритмы и подпрограммы

Работа 3.5. Программирование с использованием подпрограмм

Работа 3.5. Программирование с использованием подпрограмм

Задание 1

Для решения всех задач сделать два варианта программы: с реализацией указанной подпрограммы в виде функции и в виде процедуры.

Уровень 1

1. Составить программу нахождения наибольшего общего делителя (НОД) и наименьшего общего кратного (НОК) двух натуральных чисел

.

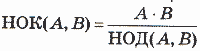Использовать подпрограмму алгоритма Евклида для определения НОД.

2. Вычислить площадь правильного шестиугольника со стороной а, используя подпрограмму вычисления площади треугольника.

3. Даны две дроби 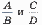— (А, В, С, D — натуральные числа).

Составить программу деления дроби на дробь. Ответ должен быть несократимой дробью. Использовать подпрограмму алгоритма Евклида для определения НОД.

4. Даны две дроби 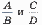— (А, В, С, D — натуральные числа).

Составить программу умножения дроби на дробь. Ответ должен быть несократимой дробью. Использовать подпрограмму алгоритма Евклида для определения НОД.

5. Даны две дроби 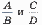— (А, В, С, D — натуральные числа).

Составить программу вычитания из первой дроби второй. Ответ должен быть несократимой дробью. Использовать подпрограмму алгоритма Евклида для определения НОД.

6. Написать программу вычисления суммы 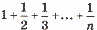— для заданного числа n. Результат представить в виде несократимой дроби 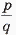(р, q — натуральные). Использовать подпрограммы алгоритма Евклида для определения НОД и сложения двух простых дробей.

7. Даны числа X, Y, Z, Т — длины сторон четырехугольника. Вычислить его площадь, если угол между сторонами длиной X и Y — прямой. Использовать две подпрограммы для вычисления площадей: прямоугольного треугольника и прямоугольника.

Задание 2

Для всех задач выделить подзадачи, решения которых могут быть реализованы через подпрограммы. Выбрать наиболее удобный вариант подпрограммы: функцию или процедуру. Составить программу решения задачи.

Уровень 2

1. Дано простое число. Найти следующее за ним простое число.

2. Для заданного натурального числа п найти наименьший нечетный натуральный делитель k (k ≠ 1).

3. Заменить данное натуральное число на число, которое получается из исходного записью его цифр в обратном порядке (например, дано число 156, нужно получить 651).

4. Найти все натуральные числа, не превосходящие заданного п, которые делятся на каждую из своих цифр.

5. Имеется часть катушки с автобусными билетами. Номер билета шестизначный. Составить программу, определяющую количество счастливых билетов на катушке, если меньший номер билета — N, больший — М (билет является счастливым, если сумма первых трех его цифр равна сумме последних трех).

6. Из заданного числа вычли сумму его цифр. Из результата вновь вычли сумму его цифр и т. д. Через сколько таких действий получится нуль?

7. На отрезке [100, А] (2¹⁰ < N < 2³¹) найти количество чисел, составленных из цифр а, b, с.

8. Найти все натуральные n-значные числа, цифры в которых образуют строго возрастающую последовательность (например, 1234,5789).

Уровень 3

9. Два простых числа называются «близнецами», если они отличаются друг от друга на 2 (например, 41 и 43). Напечатать все пары «близнецов» из отрезка [n, 2n], где n — заданное натуральное число, большее 2.

10. Дано четное число n > 2. Проверить для него гипотезу Гольдбаха: каждое четное п представляется в виде суммы двух простых чисел.

11. Составить программу разложения данного натурального числа на простые множители. Например, 200 = 2³ • 5².

12. Дано натуральное число n. Найти все меньшие п числа Мерсенна. (Простое число называется числом Мерсенна, если оно может быть представлено в виде 2^p — 1, где р — тоже простое число. Например, 31 = 2⁵ - 1 — число Мерсенна.)

13. Два натуральных числа называются «дружественными», если каждое из них равно сумме всех делителей (кроме его самого) другого (например, числа 220 и 284). Найти все пары «дружественных» чисел, которые не больше данного числа N.

14. Натуральное число, в записи которого n цифр, называется числом Армстронга, если сумма его цифр, возведенная в степень n, равна самому числу. Найти все числа Армстронга от 1 до k.

15. Найти все простые натуральные числа, не превосходящие n, двоичная запись которых представляет собой палиндром, т. е. читается одинаково слева направо и справа налево.

16. Составить программу для нахождения чисел из интервала [М, N], имеющих наибольшее количество делителей.

17 Дано натуральное число n > 1. Определить длину периода десятичной записи дроби 1/n.

Следующая страница Подпрограммы