Уроки 17 - 18
Логика и компьютер. Логические операции. Диаграммы Эйлера-Венна
§18. Логика и компьютер. §19. Логические операции. §20. Диаграммы
Содержание урока
§18. Логика и компьютер
§19. Логические операции
§20. Диаграммы
Диаграммы Венна или круги Эйлера
Задачи
§20. Диаграммы
Задачи
Задача 1. Известно количество страниц, которые находит поисковый сервер по следующим запросам (здесь символ «&» обозначает операцию «И», а «|» — операцию «ИЛИ»):
собаки | кошки 770
кошки 550
собаки & кошки 100
Сколько страниц будет выдано по запросу собаки?
Сначала попробуем рассмотреть задачу в общем виде и вывести формулу для её решения. Построим диаграмму с двумя областями А и В. Эти области могут быть разделены (рис. 3.16, а) или пересекаться (рис. 3.16, б).
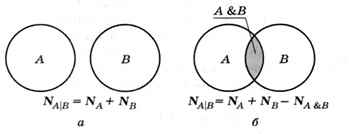
Рис. 3.16
Обозначим через Nx число страниц, которые выдаются по запросу X. В первом случае, когда области не пересекаются, получаем очевидную формулу: NA|B = NA + NB- Это значит, что количество страниц, полученных по запросу А | В, будет равно сумме результатов по отдельным запросам.
Во втором случае (рис. 3.16, б) сумма NA + NB дважды включает общую область, т. е. результат запроса А & В. Поэтому формула изменяется:
NA|B = NA + NB - N А&B.
Это более общий случай, справедливый и для рис. 3.16, а, где N А&B =0. Для нашей задачи (область А — собаки, область В — кошки) получаем:
NA = NA|B - NB + N А&B = 770 - 550 + 100 = 320.
Рассмотрим теперь более сложную задачу, с тремя областями.
Задача 2. Известно количество страниц, которые находит поисковый сервер по следующим запросам (здесь символ «&» обозначает операцию «И», а «|» — операцию «ИЛИ»):
собаки 200
кошки 250
лемуры 450
кошки | собаки 450
кошки | лемуры 40
собаки | лемуры 50
Сколько страниц найдёт этот сервер по запросу
(кошки | собаки) & лемуры?
Обозначим буквами С, К и Л области (группы сайтов), содержащие ключевые слова «собаки», «кошки» и «лемуры» соответственно (рис. 3.17). Построим диаграмму с тремя переменными и выделим интересующую область, которая соответствует запросу
(кошки | собаки) & лемуры?
.На рисунке 3.17 эта область закрашена серым цветом.
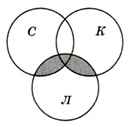
Рис. 3.17
В общем виде задача очень сложна. Попробуем найти какое-нибудь упрощающее условие. Например, выделим три условия:
собаки 200
кошки 250
кошки & собаки 450
Это означает, что область «кошки ИЛИ собаки» равна сумме областей «кошки» и «собаки», т. е. эти области не пересекаются! Таким образом, в нашем случае диаграмма выглядит, как показано на рис. 3.18.
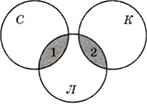
Рис. 3.18
Области 1 (собаки & лемуры) и 2 (кошки & лемуры) нам известны, они составляют соответственно 40 и 50 страниц, поэтому по запросу (кошки | собаки) & лемуры поисковый сервер выдаст 40 + 50 = 90 страниц.
Подготовьте сообщение
а) «Диаграммы Венна и теория множеств»
б) «Язык запросов поисковых систем»
Задачи для самостоятельной работы
Следующая страница 
§18. Логика и компьютер
Cкачать материалы урока
