Урок 23
Хранение в памяти целых и вещественных чисел
§26. Особенности представления чисел в компьютере. §27. Хранение в памяти целых чисел. §29. Хранение в памяти вещественных чисел
Содержание урока
§26. Особенности представления чисел в компьютере
§27. Хранение в памяти целых чисел
§29. Хранение в памяти вещественных чисел
Как кодируются в компьютерах вещественные числа?
Представление чисел с плавающей запятой
Два способа представления чисел с плавающей запятой
§29. Хранение в памяти вещественных чисел
Представление чисел с плавающей запятой
Удобное представление вещественных чисел не пришлось специально придумывать. В математике уже существовал подходящий способ записи, основанный на том, что любое число А в системе счисления с основанием В можно записать в виде
A = ± Z • ВР,
где Z называют значащей частью, а показатель степени Р — порядком числа (рис. 4.19). Для десятичной системы это выглядит привычно, например, заряд электрона равен -1,6 • 10-19 кулона, а скорость света в вакууме составляет 3 • 108 м/с.
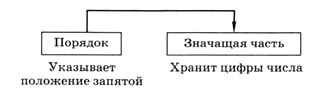
Рис. 4.19
Однако представление числа с плавающей запятой не единственно. Например, число 23,4 можно записать следующими способами:
2340 • 10-2 = 234 • 10-1 = 23,4 • 100 = 2,34 • 101 = 0,234 • 102 = 0,0234 • 103 = ...
На первый взгляд, выбор очень широкий, однако большинство вариантов обладают серьезными недостатками. В частности, все представления, в которых значащая часть содержит нули непосредственно после запятой (0,0234, 0,00234 и т. п.) или перед ней (2340, 23400 и т. п.), не подходят, поскольку, сохраняя эти незначащие нули, мы напрасно увеличиваем разрядность чисел. Согласно математической теории, для обеспечения максимальной точности при сохранении цифр числа в фиксированном количестве разрядов надо выбирать такой метод, при котором значащие цифры числа следует поместить как можно ближе к запятой. С этой точки зрения оптимальным будет вариант, когда целая часть равна нулю, а первая ненулевая цифра находится сразу после запятой (в нашем примере 0,234). При этом вместо двух частей (целой и дробной) остаётся только дробная, что фактически делает ненужной «разделительную» запятую. Но взгляните на рис. 4.20, а, изображающий такое число на индикаторе: первый разряд всегда равен нулю, что делает его практически бесполезным. Поэтому с точки зрения экономии разрядов лучше взять другой вариант, в котором значащая часть равна 2,34 (рис. 4.20, б). Именно такой выбор закреплён в стандарте IEEE 754 1, на котором основана арифметика вещественных чисел в современных компьютерах.
1 Последняя версия стандарта называется IEEE 754-2008.
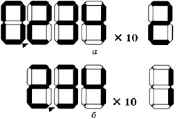
Рис. 4.20
Следующая страница 
Два способа представления чисел с плавающей запятой
Cкачать материалы урока
