Уроки 36 - 39
Логические величины и выражения, программирование ветвлений
Практикум
Практическая работа № 3.2
"Программирование логических выражений"
Практическая работа № 3.3
"Программирование ветвящихся алгоритмов"

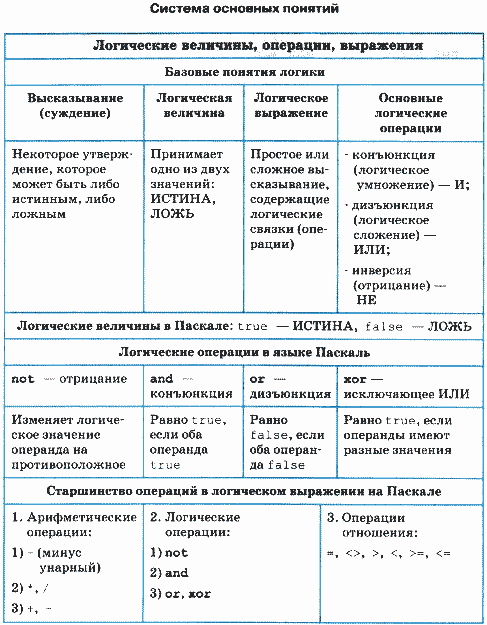
Логические величины, операции, выражения

С элементами математической логики вы уже встречались в курсе информатики основной школы, изучая способы записи запросов к базе данных и условной функции ЕСЛИ в электронных таблицах, основы алгоритмизации и программирования. Повторим основные понятия логики с целью дальнейшего углубления ваших знаний в использовании ее для программирования.

К числу основных понятий логики относятся: высказывание, логическая величина, логические операции, логические выражения и формулы.

Высказывание (суждение) — это повествовательное предложение, в котором что-либо утверждается или отрицается. По поводу любого высказывании можно сказать, истинно оно или ложно.

Например, высказывание «На улице идет дождь» будет истинным или ложным в зависимости от состояния погоды в данный момент. Истинность высказывания «Значение А больше, чем В», записанного в форме неравенства: А > В, будет зависеть от значений переменных А и В.

Логические величины — понятия, выражаемые словами: ИСТИНА, ЛОЖЬ (true, false). Следовательно, истинность высказываний выражается через логические величины.

Логическая константа: ИСТИНА или ЛОЖЬ.

Логическая переменная: символически обозначенная логическая величина. Следовательно, если известно, что А, В, X, Y и др. — переменные логические величины, то, значит, они могут принимать значения только ИСТИНА или ЛОЖЬ.

Логическое выражение — простое или сложное высказывание. Сложное высказывание строится из простых с помощью логических операций (связок).

Логические операции

Конъюнкция (логическое умножение). В русском языке она выражается союзом И. В математической логике используются знаки & или ∧. Конъюнкция — двухместная операция; записывается в виде: А & В. Значением такого выражения будет ЛОЖЬ, если значение хотя бы одного из операндов ложно.

Дизъюнкция (логическое сложение). В русском языке этой связке соответствует союз ИЛИ. В математической логике она обозначается знаком v. Дизъюнкция — двухместная операция; записывается в виде: A v В. Значением такого выражения будет ИСТИНА, если значение хотя бы одного из операндов истинно.

Отрицание. В русском языке этой связке соответствует частица НЕ (в некоторых высказываниях применяется оборот «неверно, что ...»). Отрицание — унарная (одноместная) операция; записывается в виде: ¬ А или Ā.

Правила выполнения рассмотренных логических операций отражены в следующей таблице, которая называется таблицей истинности логических операций (здесь И означает «истина», Л — «ложь»):

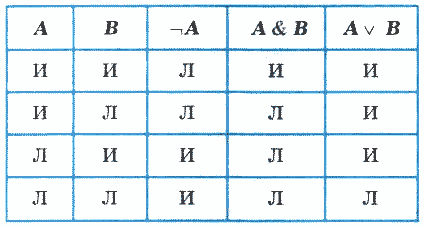
Логическая формула — формула, содержащая лишь логические величины и знаки логических операций. Результатом вычисления логической формулы является ИСТИНА или ЛОЖЬ.

Последовательность выполнения операций в логических формулах определяется старшинством операций. В порядке убывания старшинства логические операции расположены так: отрицание, конъюнкция, дизъюнкция. Кроме того, на порядок выполнения операций влияют скобки, которые можно использовать в логических формулах.

Например: (А & В) v (¬ А & В) v (¬ А & ¬ В).

Пример. Вычислить значение логической формулы:

¬ X & Y v X & Z,

если логические переменные имеют следующие значения: X = ЛОЖЬ, Y = ИСТИНА, Z = ИСТИНА.

Решение. Отметим цифрами сверху порядок выполнения операций в формуле:

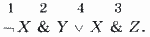
Используя таблицу истинности, вычислим формулу по шагам:

1)	 ЛОЖЬ = ИСТИНА;
2)	 ИСТИНА & ИСТИНА = ИСТИНА;
3)	 ЛОЖЬ & ИСТИНА = ЛОЖЬ;
4)	 ИСТИНА v ЛОЖЬ = ИСТИНА.
Ответ: ИСТИНА.

Логические функции на области числовых значений

Алгебра чисел пересекается с алгеброй логики в тех случаях, когда приходится проверять принадлежность значений алгебраических выражений некоторому множеству. Например, принадлежность значения числовой переменной X множеству положительных чисел выражается через высказывание: «X больше нуля». Символически это записывается так: Х > 0. В алгебре такое выражение называют неравенством. В логике — отношением.

Отношение X > 0 может быть истинным или ложным. Если X — положительная величина, то оно истинно, если отрицательная, то ложно. В общем виде отношение имеет следующую структуру:

< выражение 1 > < знак отношения > < выражение 2 >

Здесь выражения 1 и 2 — некоторые математические выражения, принимающие числовые значения. В частном случае выражение может представлять собой одну константу или одну переменную величину. Знаки отношений могут быть следующими:

Итак, отношение — это простое высказывание, а значит, логическая величина. Оно может быть как постоянной: 5 > 0 — всегда ИСТИНА, 3 * 6 : 2 — всегда ЛОЖЬ; так и переменной: а < b, х + 1 = с - d. Если в отношение входят переменные числовые величины, то и значение отношения будет логической переменной.

Отношение можно рассматривать как логическую функцию от числовых аргументов. Например: F(x) = (х > 0) или Р(х, у) = = (х < у). Аргументы определены на бесконечном множестве действительных чисел, а значения функции — на множестве, состоящем из двух логических величин: ИСТИНА, ЛОЖЬ.

Логические функции от числовых аргументов еще называют термином предикат. В алгоритмах предикаты играют роль условий, по которым строятся ветвления и циклы. Предикаты могут быть как простыми логическими функциями, не содержащими логических операций, так и сложными, содержащими логические операции.

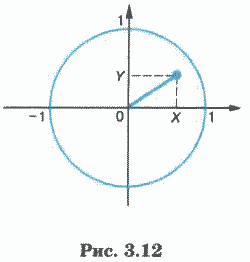
Пример 1. Записать предикат (логическую функцию) от двух вещественных аргументов X и Y, который будет принимать значение ИСТИНА, если точка на координатной плоскости с координатами X и Y лежит внутри единичной окружности с центром в начале координат (рис. 3.12).

Из геометрических соображений понятно, что для всех точек, лежащих внутри единичной окружности, будет истинным значение следующей логической функции:

F(Х, У) = (X² + У² < 1).

Для значений координат точек, лежащих на окружности и вне ее, значение функции F будет ложным.

Пример 2. Записать предикат, который будет принимать значение ИСТИНА, если точка на координатной плоскости с координатами X и У лежит внутри кольца с центром в начале координат, и радиусами R1 и R2.

Поскольку значения R1 и R2 — переменные величины, искомая логическая функция будет иметь четыре аргумента: X, У, R1, R2. Возможны две ситуации:

1) R1² < X² + У² < R2² и R1 < R2: R1 — внутренний радиус, R2 — внешний радиус;

2) R2² < X² + У² < R1² и R2 < R1: R2 — внутренний радиус, R1 — внешний радиус.

Объединив дизъюнкцией оба этих утверждения и записав их по правилам алгебры логики, получим следующую логическую функцию:

F(Х, У, R1, R2) = (((X² + У²) > R1²) & ((X² + У²) < R2²) & R1 < R2) v (((X² + У²) > R2²) & ((X² + У²) < R1²) & R2 < R1).

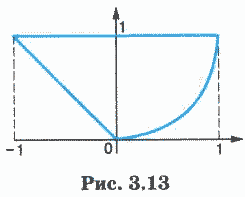
Пример 3. Записать предикат, который будет принимать значение ИСТИНА, если точка на координатной плоскости с координатами X и У лежит внутри фигуры, ограниченной жирными линиями на рис. 3.13.

Фигура ограничена тремя границами, описываемыми уравнениями:

У = -X — левая граница, линейная функция;

У = 1 — верхняя граница, константа;

У = X² — правая граница, парабола.

Рассматриваемая область есть пересечение трех полуплоскостей, описываемых неравенствами:

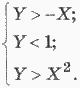
Во внутренних точках все эти три отношения являются одно-временно истинными. Поэтому искомый предикат имеет вид:

F(X, У) = (У > -X) & (Y < 1) & (У > X²).

Логические выражения на Паскале

Уже говорилось о том, что в Паскале имеется логический тип данных.

Логические константы: true (истина), false (ложь).

Логические переменные: описываются с типом Boolean.

Операции отношения: осуществляют сравнение двух операндов и определяют, истинно или ложно соответствующее отношение между ними. Знаки операций отношения: = (равно), <> (не равно), > (больше), < (меньше), >= (больше или равно), <= (меньше или равно).

Логические операции: not — отрицание, and — логическое умножение (конъюнкция), or — логическое сложение (дизъюнкция), хоr — исключающее ИЛИ. Таблица истинности для этих операций (Т — true; F — false):

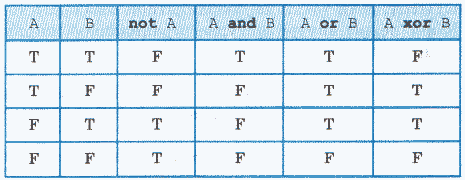
Логическое выражение может состоять из логических констант и переменных, отношений, логических операций. Логическое выражение принимает значение true или false.

Например, логическая формула ¬ X & У v X & Z на Паскале запишется в виде следующего логического выражения:

not X and Y or X and Z,

где X, Y, Z — переменные типа Boolean.

Логические операции располагаются в следующем порядке по убыванию старшинства (приоритета): 1) not, 2) and, 3) or, xor. Операции отношения имеют самый низкий приоритет. Поэтому если операндами логической операции являются отношения, то их следует заключать в круглые скобки. Например, математическому неравенству 1 ≤ X ≤ 50 соответствует следующее логическое выражение:

(1 <= Х) and (Х <= 50)

Логическая функция odd(x) принимает значение true, если значение целочисленного аргумента х является нечетным, иначе — false.

Для правильной записи сложного логического выражения (предиката) нужно учитывать относительные приоритеты арифмети-ческих, логических операций и операций отношений, поскольку все они могут присутствовать в логическом выражении. По убыванию приоритета операции располагаются в следующем порядке.

1.	 Арифметические операции:
- (минус унарный)
*, /
+, -
2.	 Логические операции:
not
and
or, xor
3.	 Операции отношения:
=, <>, >, <, >=, <=

Еще раз обратите внимание, что в логическом выражении, соответствующем предикату из примера 3:

(Y > -X) and (Y < 1) and (Y > X * X),

операции отношения заключены в скобки, поскольку они младше логических операций, а выполняться должны раньше.

Вопросы и задания

1. Какого типа величина получается при вычислении отношения (неравенства) между числами?

2. Что такое предикат? Приведите примеры.

3. Запишите на языке алгебры логики логические функции, которые будут принимать значение ИСТИНА, если справедливы следующие утверждения, и ЛОЖЬ — в противном случае:

а) все числа X, Y, Z равны между собой;
б) из чисел X, Y, Z только два равны между собой;
в) каждое из чисел X, Y, Z положительно;
г) только одно из чисел X, У, Z положительно;
д) значения чисел X, У, Z упорядочены по возрастанию.

4. Все формулы, полученные при решении предыдущей задачи, запишите в виде логических выражений на Паскале.

5. Постройте таблицу истинности для логической формулы:

¬X & Y v X & Z.

Пояснение: в таблице истинности должны быть вычислены значения формулы для всех вариантов значений логических переменных: X, У, Z. Следовательно, таблица будет содержать 2³ = 8 строк и 4 столбца: значения X, У, Z и результат. В таблицу можно добавить дополнительные столбцы, содержащие результаты промежуточных операций.

6. Вычислите значения следующих логических выражений, записанных на Паскале:

Пояснения: odd(x) — логическая функция определения четности аргумента, равна true, если х — нечетное, и равна false, если х — четное; trunc (х) — целочисленная функция от вещественного аргумента, возвращающая ближайшее целое число, не превышающее х по модулю.

Программирование ветвлений

На уроках 33 - 35 "Программирование линейных алгоритмов" был показан способ отображения ветвления (полного и неполного) на блок-схеме и учебном Алгоритмическом языке. Алгоритмическая структура ветвления программируется в Паскале с помощью условного оператора If. В 9 классе вы познакомились с этим оператором. Вспомним его формат.

Полное ветвление:

If < логическое выражение >
Then < оператор 1 >
Else < оператор 2 >

Неполное ветвление:

If < логическое выражение >
Then < оператор >

То, что в алгоритмах называется условием, в Паскале является логическим выражением, которое вычисляется в первую очередь. Если его значение равно true, то будет выполняться < оператор 1 > (после Then), если — false, то < оператор 2 > (после Else) для полной формы или оператор, сразу следующий после условного, для неполной формы (без Else). На ветвях может быть как простой оператор, так и составной — серия операторов в операторных скобках Begin, End.

Пример 1. По длинам трех сторон треугольника а, b, с требуется вычислить его площадь.

Для решения задачи используется формула Герона

где р = (а + b + с)/2 — полупериметр треугольника. Исходные данные должны удовлетворять основному соотношению для сторон треугольника — длина каждой стороны должна быть меньше суммы длин двух других сторон, и длины сторон не могут быть отрицательными величинами.

Имея возможность в одном условном операторе записывать достаточно сложные логические выражения, используя логические операции, мы можем сразу «отфильтровать» все варианты неверных исходных данных.

Пример 2. Требуется перевести пятибалльную оценку в ее на-именование: 5 — «отлично», 4 — «хорошо», 3 — «удовлетворительно», 2 — «неудовлетворительно».

Блок-схема алгоритма приведена на рис. 3.14.

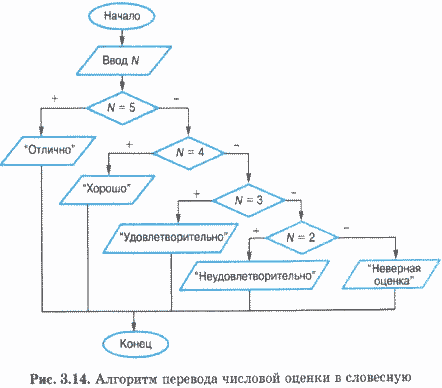
Этот алгоритм имеет структуру вложенных ветвлений и может быть запрограммирован с использованием условного оператора If следующим образом:

Пример 3. Решение рассмотренной в предыдущем примере задачи можно запрограммировать с помощью одного оператора выбора, имеющегося в языке Паскаль. Вот как будет выглядеть такая программа:

Оператор выбора имеет следующий формат:

Case <  селектор > of
< список констант 1 > :	< оператор 1 > ;
···
< список констант N > :	< оператор N > ;
Else <оператор>
End

Здесь < селектор > — это выражение любого порядкового типа; < константа > — постоянная величина того же типа, что и селектор; < оператор > — любой простой или составной оператор.

Выполнение оператора выбора происходит так: вычисляется выражение-селектор; затем в списках констант ищется такое значение, которое совпадает с полученным значением селектора; далее исполняется оператор, помеченный данной константой. Если такой константы не найдено, то происходит переход к выполнению оператора, следующего после слова Else.

Пример 4. В этом примере демонстрируется использование списка констант в операторе выбора. Программа сообщает, сдал студент экзамен или не сдал. Если оценка одна из следующих: 3, 4, 5, то экзамен сдан; если 2, то не сдан.

Case N of
	3,	4,	5:	WriteLn('Экзамен сдан');
			2:	WriteLn('Экзамен не сдан');
	Else WriteLn('Нет такой оценки')
End

Так же как условный оператор, оператор выбора может ис-пользоваться в неполной форме, т. е. без ветви Else.

Если применить условный оператор, то эта программа запишется так:

If (N=3) or (N=4) or (N=5)
Then WriteLn('Экзамен сдан')
Else If N=2
	Then WriteLn('Экзамен не сдан')
	Else WriteLn('Нет такой оценки');

В условии ветвления использовано сложное логическое выражение, содержащее операции логического сложения or (или).

Вопросы и задания

1. Какие операторы используются для программирования ветвящихся алгоритмов?

2. В каких случаях удобно использование оператора выбора?

3. Составьте на Паскале программу упорядочения по возрастанию значений в трех переменных: X, Y, Z.

4. Используя оператор выбора, составьте программу, которая по введенному номеру месяца будет выводить название соответствующего времени года (зима, весна, лето, осень).

Пример поэтапной разработки программы решения задачи

Постановка задачи и формализация

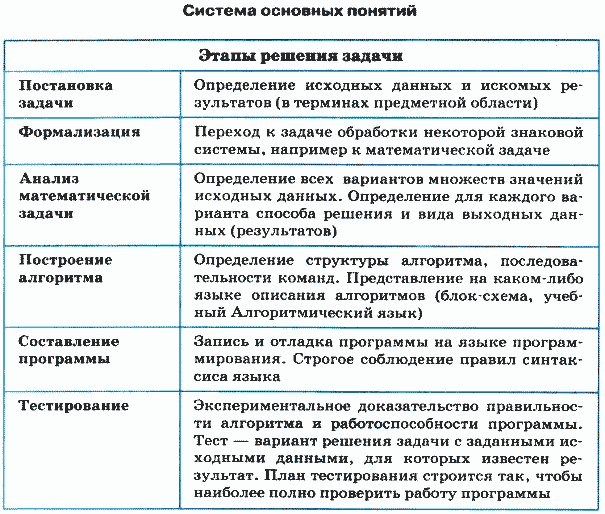
Словом «задача» называют проблему, которая требует решения. Решение задачи начинается с ее постановки. На этапе постановки задачи в терминах предметной области (физики, экономики, биологии и др.) определяются исходные данные и результаты, которые надо получить.

Следующий этап — формализация задачи. Чаще всего процесс формализации означает перевод задачи на язык математики: формул, уравнений, неравенств, систем уравнений, систем неравенств и т. п.

Подробнее о формализации будет рассказано в разделе, посвященном информационному моделированию (в 11 классе). Некоторые представления об этом вы уже имеете из курса информатики для 7-9 классов.

Решение полученной математической задачи требует знания математики, умения выполнять анализ математической задачи. Такой анализ необходим для того, чтобы построить правильный алгоритм решения, обладающий всеми свойствами алгоритма.

Анализ математической задачи

Пусть в результате формализации некоторой задачи было получено квадратное уравнение: ах² + bх + с = 0, где коэффициенты а, b, с являются исходными данными. Требуется решить это уравнение, т. е. найти его корни. Проведем анализ этой математической задачи.

Рассмотрим различные варианты значений исходных данных, которые приводят к разным результатам для решающего ее алгоритма. Ограничимся только поиском вещественных корней уравнения.

Проанализируем все возможные варианты множества значений коэффициентов а, b, с:

Построение алгоритма

Построим блок-схему алгоритма решения квадратного уравнения (рис. 3.15), учитывающего все ситуации, описанные в анализе задачи. Здесь вместо слов «да» и «нет» использованы знаки « + » и « — ».

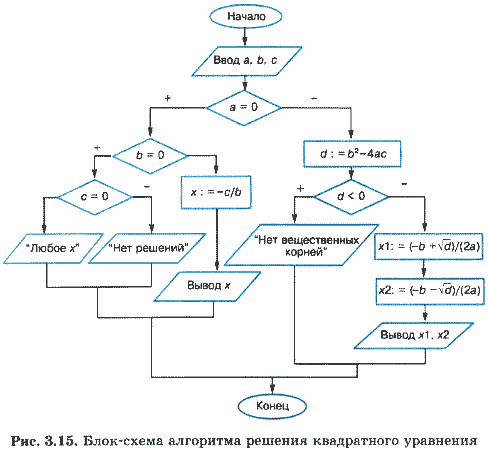
Построенный алгоритм, несомненно, удовлетворяет свойству универсальности по отношению к исходным данным. Запишем этот же алгоритм на учебном Алгоритмическом языке.

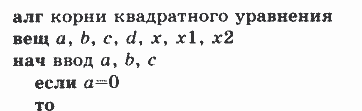
Обратите внимание на смещения строк в тексте алгоритма — соблюдается принцип структуризации внешнего вида ("Программирование линейных алгоритмов"). Повторим его: запись всякой вложенной структуры должна быть смещена на несколько позиций вправо относительно записи внешней структуры, а конструкции одного уровня вложенности записываются на одном вертикальном уровне.

Программирование

Алгоритмический язык (АЯ) — это язык описания алгоритмов с русскими служебными словами. После того как алгоритм записан на АЯ, составление программы на Паскале становится несложной задачей. Основное внимание следует уделять строгому соблюдению синтаксических правил языка. Правило смещения строк в тексте программы то же, что было сформулировано (в "Программирование линейных алгоритмов") для АЯ. Соответствующие друг другу служебные слова Begin и End должны располагаться друг под другом.

Чем больше текст программы, тем больше вероятность совершения ошибок при ее записи и вводе в компьютер. Ошибки, нарушающие правила грамматики языка, называются синтаксическими ошибками. Поиск и устранение синтаксических ошибок в программе называются отладкой. Отладить программу программисту помогает система программирования на данном языке, которая автоматически обнаруживает ошибки и сообщает о них программисту.

Тестирование программы

Тестирование — это этап, на котором экспериментально доказывается правильность алгоритма, заключенного в программе, и работоспособность программы. Тест — это вариант решения задачи с заданными исходными данными, для которых известен результат.

Предварительно должен быть составлен план тестирования. Для ветвящегося алгоритма должны быть протестированы все его ветви. В нашем примере пять ветвей, пять вариантов ответа. Значит, в плане тестирования должно быть не менее пяти вариантов теста.

В таблице 3.5 представлен план тестирования программы Roots и результаты проведенного тестирования.

Теперь, анализируя результаты тестирования, делаем вывод: правильность алгоритма и работоспособность программы доказаны.

Если какой-то из вариантов теста не дает ожидаемого результата, то в программе есть ошибки. Например, пусть программист ошибочно записал следующие операторы присваивания для вычисления корней:

Результаты всех тестов, кроме 4-го, совпали с ожидаемыми, а в 4-м тесте получилось: х1 = 4, х2 = -6. После этого программист обратит внимание на выражения для вычисления корней и исправит ошибки: либо заменит знак умножения на знак деления, либо заключит в скобки выражение 2*а.

Вопросы и задания

1. Сформулируйте основные цели этапов алгоритмического решения задачи.

2. Проанализируйте задачу решения биквадратного уравнения, составьте алгоритм и напишите программу на Паскале.

---

Практикум

Работа 3.2. Программирование логических выражений

Задание

Для каждой задачи составить программу, выводящую значение TRUE, если указанное высказывание является истинным, и FALSE — в противном случае (использовать условный оператор нельзя).

Уровень 1

1. Треугольник со сторонами а, b, с является равносторонним.

2. Целое число N является четным двузначным числом.

3. Треугольник со сторонами а, b, с является равнобедренным.

4. Среди чисел а, b, с есть хотя бы одна пара взаимно противоположных чисел.

5. Данные числа х, у являются координатами точки, лежащей в первой координатной четверти.

6. Данные числа c и d являются соответственно квадратом и кубом числа а.

7. Заданное натуральное число N является двузначным и кратно К.

Уровень 2

8. (х₁, у₁) и (х₂, у₂) — координаты левой верхней и правой нижней вершин прямоугольника. Точка А(х, у) принадлежит данному прямоугольнику.

9. Данное четырехзначное число читается одинаково слева направо и справа налево.

10. В заданном натуральном трехзначном числе N имеется четная цифра.

11. Сумма каких-либо двух цифр заданного трехзначного натурального числа N равна третьей цифре.

12. Сумма цифр заданного четырехзначного числа N превосходит произведение цифр этого же числа на 1.

13. Сумма двух последних цифр заданного трехзначного числа N меньше заданного К, а первая цифра больше 5.

Уровень 3

14. Целая и дробная части заданного вещественного числа одинаковы.

15. Заданы координаты трех точек плоскости. Эти точки не лежат на одной прямой.

16. Первые две цифры в дробной части заданного вещественного числа совпадают с записью целой части этого числа.

17. Точка с координатами (х, у) принадлежит части плоскости, лежащей между прямыми у = m, у = п (m < n).

18. Среди первых трех цифр из дробной части положительного вещественного числа есть нуль.

19. Шахматный король за один ход может переместиться с одного заданного поля на другое (каждое поле задано двумя координатами — целыми числами от 1 до 8).

20. Шахматный ферзь за один ход может переместиться с одного заданного поля на другое (каждое поле задано двумя координатами — целыми числами от 1 до 8).

Работа 3.3. Программирование ветвящихся алгоритмов

Задание 1

Для каждой задачи составить программу с ветвящейся структурой, используя условный оператор IF.

Уровень 1

1. Даны два угла треугольника (в градусах). Определить, существует ли такой треугольник. Если да, то прямоугольный ли он.

2. На плоскости XOY задана своими координатами точка А. Указать, где она расположена: на какой оси или в какой координатной четверти.

3. Грузовой автомобиль выехал из одного города в другой со скоростью υ₁ км/ч. Через Ив этом же направлении выехал легковой автомобиль со скоростью υ₂ км/ч. Составить программу, определяющую, догонит ли легковой автомобиль грузовой через t₁ ч после своего выезда.

4. Написать программу нахождения суммы большего и меньшего из 3 чисел.

5. Написать программу, распознающую по длинам сторон среди всех треугольников прямоугольные. Если таковых нет, то вычислить величину угла С.

6. Найти max{min(a, b), min(c, d)}.

7. Составить программу, осуществляющую перевод величин из радианной меры в градусную или наоборот. Программа должна запрашивать, какой перевод нужно осуществить, и выполнять указанное действие.

Уровень 2

8. Заданы размеры А, В прямоугольного отверстия и размеры x, y, z кирпича. Определить, пройдет ли кирпич через отверстие.

9. Два прямоугольника, расположенные в первом квадранте, со сторонами, параллельными осям координат, заданы координатами своих левого верхнего и правого нижнего углов. Для первого прямоугольника это точки (х₁, у₁) и (х₂, 0), для второго — (х₃, у₃), (х₄, 0). Составить программу, определяющую, пересекаются ли данные прямоугольники, и вычисляющую площадь общей части, если они пересекаются.

10. В небоскребе N этажей и всего один подъезд; на каждом этаже по 3 квартиры; лифт может останавливаться только на нечетных этажах. Человек садится в лифт и набирает номер нужной ему квартиры М. На какой этаж должен доставить лифт пассажира?

11. Написать программу, которая по заданным трем числам определяет, является ли сумма каких-либо двух из них положительной.

12. Известно, что из четырех чисел а₁, а₂, а₃ и а₄ одно отлично от трех других, равных между собой; присвоить номер этого числа переменной n.

13. Составить программу, которая проверяла бы, не приводит ли суммирование двух целых чисел А и В к переполнению (т. е. к результату большему, чем 32 767). Если будет переполнение, то сообщить об этом, иначе вывести сумму этих чисел.

Уровень 3

14. Заданы координаты (на плоскости) вершин четырехугольника. Определить, является ли он: а) ромбом; б) параллелограммом; в) прямоугольником; г) квадратом.

15. Для двух треугольных пирамид, заданных ребрами, определить, площадь полной поверхности которой из них больше и на сколько.

16. Дана точка А(х, у). Определить, принадлежит ли она треугольнику с вершинами в точках (х₁, у₁), (х₂, y₂), (х₃, у₃).

17. Написать программу, определяющую, будут ли прямые А₁х + В₁у + C₁ = 0 и А₂Х + В₂у + С₂ = О перпендикулярны. Если нет, то найти угол между ними.

18. Заданы координаты вершин прямоугольника: (х₁, у₁), (х₂, у₂), (х₃, у₃), (х₄, у₄). Определить площадь части прямоугольника, расположенной в I координатной четверти.

19. Найти координаты точек пересечения прямой у = kx + b и окружности радиуса R с центром в начале координат. В каких координатных четвертях находятся точки пересечения? Если точек пересечения нет или прямая касается окружности, выдать соответствующее сообщение.

20. Дана точка А(х, у). Определить, принадлежит ли она прямоугольнику с вершинами в точках (x₁, у₁), (х₂, у₂), (х₃, у₃), (x₄, у4)

Задание 2
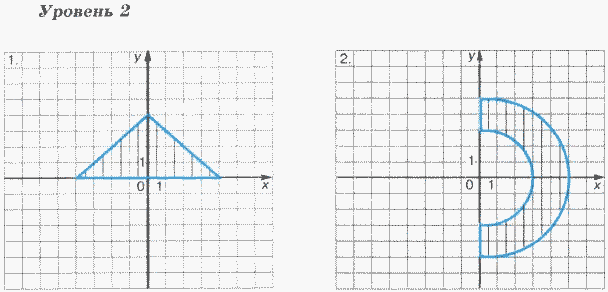
Задачи на определение принадлежности точки области

Для каждой задачи составить программу, содержащую ветвления и определяющую, принадлежит ли точка с координатами (X, Y) заштрихованной области.

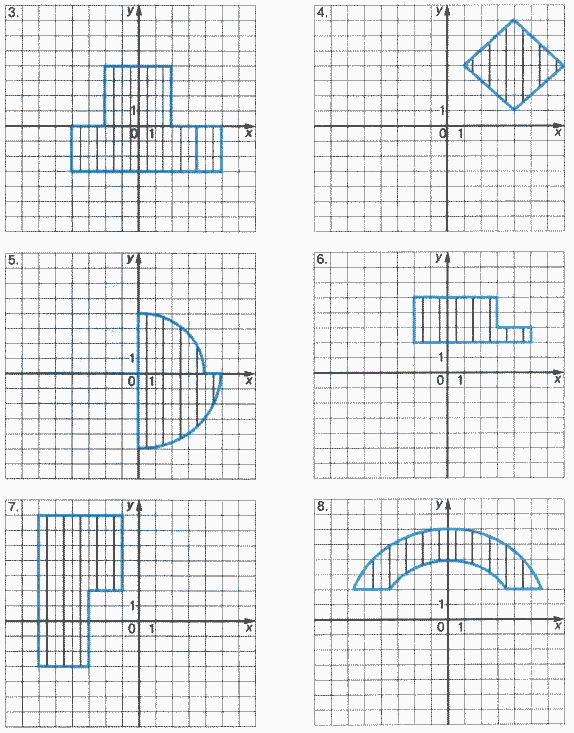
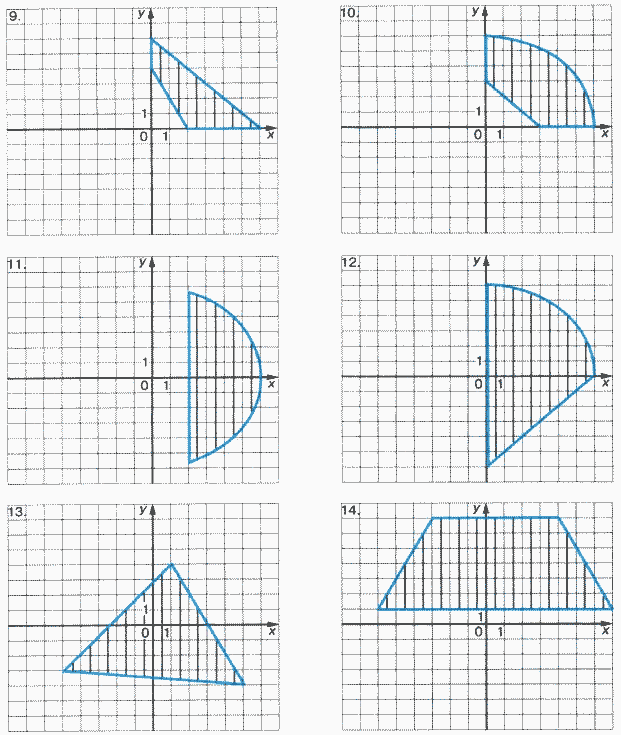
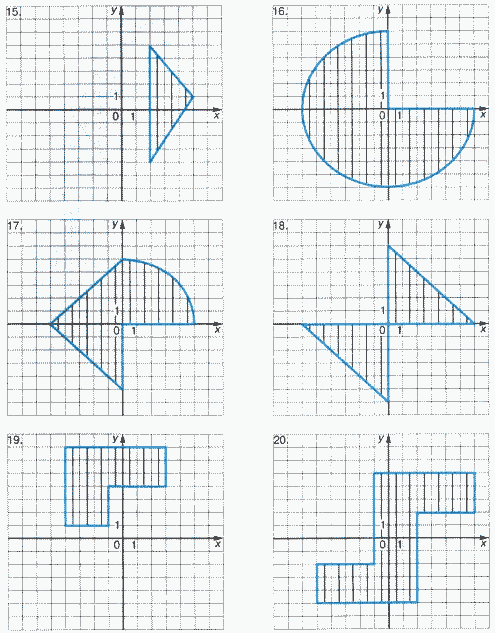
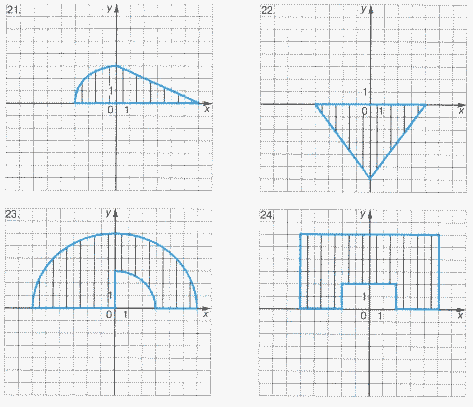
Задание 3
Задачи на использование оператора выбора

Для каждой задачи составить программу с ветвящейся структурой, используя оператор выбора SELECT CASE.

Уровень 1

1. Для каждой введенной цифры (0—9) вывести соответствующее ей название на английском языке (0 — zero, 1 — one, 2 — two, ...).

2. Составить программу, которая по данному числу (1-12) выводит название соответствующего ему месяца на английском языке.

3. Написать программу, которая по вводимому числу от 1 до 11 (номеру класса) выдает соответствующее сообщение «Привет, k-классник». Например, если k — 1, «Привет, первоклассник»; при k = 4: «Привет, четвероклассник».

4. Составить программу, позволяющую получить словесное описание школьных отметок (1 — плохо, 2 — неудовлетворительно, 3 — удовлетворительно, 4 — хорошо, 5 — отлично).

5. Написать программу, которая бы по введенному номеру единицы измерения (1 — дециметр, 2 — километр, 3 — метр, 4 — миллиметр, 5 — сантиметр) и длине отрезка L выдавала соответствующее значение длины отрезка в метрах.

6. Написать программу, которая бы по введенному номеру единицы измерения (1 — килограмм, 2 — миллиграмм, 3 — грамм, 4 — тонна, 5 — центнер) и массе М выдавала соответствующее значение массы в килограммах.

7. Даны два действительных положительных числа х и у. Арифметические действия над числами пронумерованы (1 — сложение, 2 — вычитание, 3 — умножение, 4 — деление). Составить программу, которая по введенному номеру выполняет то или иное действие над числами.

8. Написать программу, которая по номеру дня недели (целому числу от 1 до 7) выдает в качестве результата расписание уроков в вашем классе в этот день.

Уровень 2

9. Составить программу, которая по заданному году и номеру месяца определяет количество дней в этом месяце.

10. Пусть элементами круга являются радиус (первый элемент), диаметр (второй элемент) и длина окружности (третий элемент). Составить программу, которая по номеру элемента запрашивала бы его соответствующее значение и вычисляла бы площадь круга.

11. Пусть элементами прямоугольного равнобедренного треугольника являются: 1) катет а; 2) гипотенуза b; 3) высота, опущенная из вершины прямого угла на гипотенузу h; 4) площадь S. Составить программу, которая по заданному номеру и значению соответствующего элемента вычисляла бы значение всех остальных элементов треугольника 12. В старояпонском календаре был принят 12-летний цикл. Годы внутри цикла носили названия животных: крысы, коровы, тигра, зайца, дракона, змеи, лошади, овцы, обезьяны, курицы, собаки и свиньи. Написать программу, которая вводит номер некоторого года и печатает его название по старояпонскому календарю. (Справка: 1996 г. — год Крысы — начало очередного цикла.)

13. Для целого числа k от 1 до 99 напечатать фразу «Мне k лет», учитывая при этом, что при некоторых значениях k слово «лет» надо заменить на слово «год» или «года». Например, 11 лет, 22 года, 51 год.

14. Написать программу, которая по введенному числу от 1 до 12 (номеру месяца) выдает все приходящиеся на этот месяц праздничные дни (например, если введено число 1, то: 1 января — Новый год, 7 января — Рождество).

15. Дано натуральное число N. Если оно делится на 4, вывести на экран ответ N = 4k (где k — соответствующее частное); если остаток от деления на 4 равен 1, N = 4k + 1; если остаток от деления на 4 равен 2, N = 4k + 2; если остаток от деления на 4 равен 3, N = 4k + 3. Например, 12 = 4 • 3, 22 = 4 • 5 + 2.

16. Пусть элементами равностороннего треугольника являются: 1) сторона а; 2) площадь S; 3) высота h; 4) радиус вписанной окружности r; 5) радиус описанной окружности R. Составить программу, которая по заданному номеру и значению соответствующего элемента вычисляла бы значение всех остальных элементов треугольника.