Уроки 40 - 44
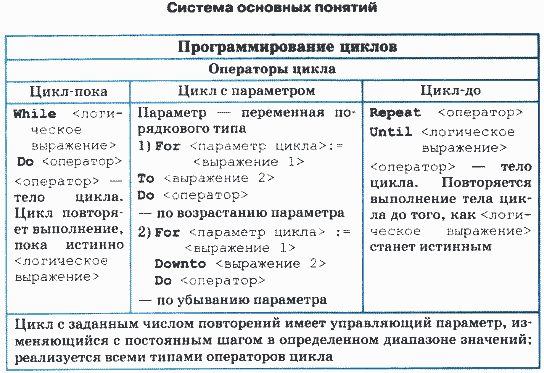
Программирование циклов
Практикум
Практическая работа № 3.4
"Программирование циклических алгоритмов"
Программирование циклов
 |
 |
 |
Рассмотрим приемы программирования циклов на Паскале. На уроках 33 - 35 "Программирование линейных алгоритмов" рассказывалось о том, что существуют две циклические алгоритмические структуры: цикл с предусловием (цикл-пока) и цикл с постусловием (цикл-до). Были показаны способы описания циклических структур в блок-схемах и на Алгоритмическом языке. Форматы соответствующих операторов цикла в Паскале следующие.
 Цикл с предусловием (цикл-пока):
Цикл с предусловием (цикл-пока):
While < логическое выражение > Do < оператор >
 Цикл с постусловием (цикл-до):
Цикл с постусловием (цикл-до):
Repeat < оператор > Until < логическое выражение >
Различают циклы с заданным числом повторений и итерационные циклы.
На примерах конкретных задач рассмотрим приемы программирования циклов.
В математике известно, что сумма следующего бесконечного числового ряда:
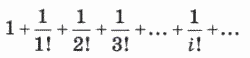
в пределе стремится к значению константы е = 2,71828182... Функция ех называется экспонентой, а логарифм по основанию е называется натуральным логарифмом: 1пх.
Требуется составить программу, вычисляющую эту константу по сумме числового ряда. Напомним, что символ «!» читается как «факториал» — функция, определенная следующим образом:
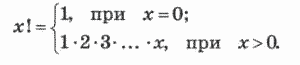
Если слагаемые в вычисляемом выражении обозначить так:
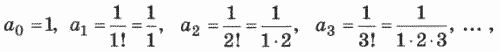
то обобщенная формула для i-го элемента будет следующей:
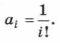
Нетрудно увидеть, что между элементами данной последовательности имеется зависимость:
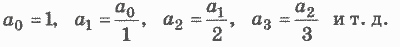
Такая зависимость называется рекуррентной зависимостью, а соответствующая числовая последовательность — рекуррентной последовательностью. Данная рекуррентная последовательность может быть описана следующей ветвящейся формулой, которая называется рекуррентной формулой:
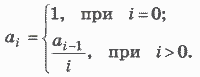
Циклы с заданным числом повторений
 Пример 1. Дано целое положительное значение N. Требуется вычислить сумму:
Пример 1. Дано целое положительное значение N. Требуется вычислить сумму:
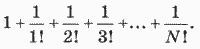
Ниже приводятся два варианта программы решения этой задачи. В первом варианте используется цикл с предусловием, во втором — цикл с постусловием.

Обратите внимание на то, как цикл с предусловием преобразуется в цикл с постусловием — условие цикла помещается после тела цикла и заменяется на противоположное:
Not(i ≤ N) = i > N.
И тот, и другой цикл повторят свое выполнение (N + 1) раз. Переменная i выполняет роль не только знаменателя в дроби 1/i!, но и является счетчиком числа повторений цикла. Такие переменные называются параметрами цикла. И еще: в цикле с постусловием служебные слова Repeat и Until сами выполняют роль операторных скобок. Поэтому писать Begin и End здесь не требуется.
Выполнение этих программ на компьютере для значения N = 7 приводит к следующему результату: Е=2,7182539.
Для программирования циклов с заданным числом повторений при постоянном шаге изменения параметра цикла в Паскале существует цикл с параметром. Вот как выглядит программа решения той же задачи с использованием цикла с параметром:

В программе используется оператор цикла For, для которого существуют два варианта:
1) For <параметр цикла>:=<выражение 1> То <выражение 2>
Do <оператор>
2) For <параметр цикла>:=<выражение 1> Downto <выражение 2>
Do <оператор>
Здесь <параметр цикла> — имя простой переменной порядкового типа. Выполнение оператора For в первом варианте (То) происходит по следующей схеме.
1. Вычисляются значения <выражения 1> и <выражения 2>. Это делается только один раз при входе в цикл.
2. Параметру цикла присваивается значение <выражения 1>.
3. Значение параметра цикла сравнивается со значением <выражения 2>. Если параметр цикла меньше или равен этому значению, то выполняется тело цикла (<оператор>), в противном случае выполнение цикла заканчивается.
4. Значение параметра цикла изменяется на следующее значение в его типе (для целых чисел — увеличивается на единицу); происходит возврат к пункту 3.
Оператор цикла For объединяет в себе действия, которые при использовании цикла While выполняют различные операторы: присваивание параметру начального значения, сравнение его с конечным значением, изменение значения параметра на следующее.
Во втором варианте оператора For слово Downto буквально можно перевести как «вниз до». В таком случае параметр цикла изменяется по убыванию, т. е. при каждом повторении цикла параметр изменяет свое значение на предыдущее (равносильно i : =pred (i)).
Работая с оператором For, учитывайте следующие правила:
• параметр цикла не может иметь вещественного типа;
• в теле цикла нельзя изменять переменную-параметр цикла;
• при выходе из цикла значение переменной-параметра является неопределенным.
Рассмотрим пример программы, в которой в теле цикла будет присутствовать ветвление.
 Пример 2. Составим программу проверки знаний учеником таблицы умножения. Компьютер задает ученику 10 вопросов на умножение чисел от 2 до 9. На каждое задание ученик вводит свой ответ, компьютер сообщает, верный ответ или нет.
Пример 2. Составим программу проверки знаний учеником таблицы умножения. Компьютер задает ученику 10 вопросов на умножение чисел от 2 до 9. На каждое задание ученик вводит свой ответ, компьютер сообщает, верный ответ или нет.
На рисунке 3.16 приведена блок-схема такого алгоритма.
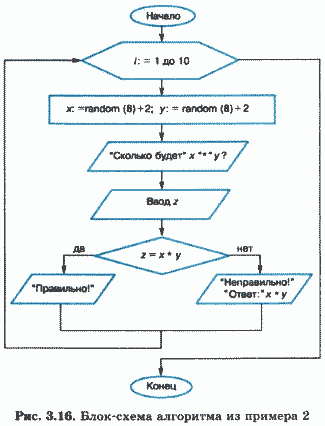
Обратите внимание на то, как отображается на блок-схеме цикл с параметром.
В этом алгоритме использована функция random (х), результатом выполнения которой является случайное целое число из диапазона от 0 до х - 1. Следовательно, выражение random (8)+2 принимает случайные значения от 2 до 9. Функция random называется датчиком случайных чисел.
На Паскале этот алгоритм программируется так:

А вот фрагмент интерфейса исполнения этой программы:
Сколько будет 4*8? 21 Неправильно! 4*8=32 Сколько будет 6*9? 54 Правильно!
В программе используется стандартная процедура randomize. Ее исполнение производит установку случайного начального состояния датчика случайных чисел. Благодаря этому при повторном выполнении программы будут получаться разные последовательности случайных чисел.
Вопросы и задания
1. Постройте трассировочную таблицу выполнения программы Summa_1 для значения n = 3.
2. Составьте программу, по которой компьютер десять раз запросит ввод любых чисел и в результате выведет среднее арифметическое значение введенных чисел (массив не использовать). Сделайте три варианта программы, используя операторы цикла While, Repeat и For.
3. Составьте программу, по которой компьютер десять раз запросит ввод целых чисел и в результате сообщит, сколько среди введенных чисел четных и сколько нечетных.
4. Составьте программу, по которой на экран будет выведена вся таблица умножения.
5. Усовершенствуйте программу TablMul (пример 2 данного параграфа) таким образом, чтобы в результате выводилось сообщение о количестве правильных и неправильных ответов.
6. Усовершенствуйте программу TablMul таким образом, чтобы в результате выводилась оценка, поставленная ученику. Критерии для выставления оценок придумайте сами.
7. Получите таблицу значений функции sin x и cos x на отрезке [0, 1] с шагом 0,1 в следующем виде:
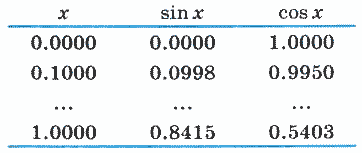
8. Получите в возрастающем порядке все трехзначные числа, в десятичной записи которых нет одинаковых цифр.
9. Значение функции е х (экспонента от х) равно сходящейся сумме бесконечного ряда:
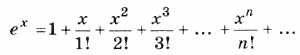
Получите рекуррентную формулу для слагаемых. Используя операторы цикла While, Repeat и For, составьте три варианта программы вычисления суммы с заданным числом слагаемых.
Вложенные и итерационные циклы
 |
 |
 |
Если в теле одного цикла имеется другой цикл, то такая структура алгоритма называется вложенными циклами. Рассмотрим задачу, программа решения которой имеет структуру вложенных циклов.
Требуется получить на экране компьютера таблицу умножения в форме матрицы Пифагора. Блок-схема алгоритма будет следующей (рис. 3.17).
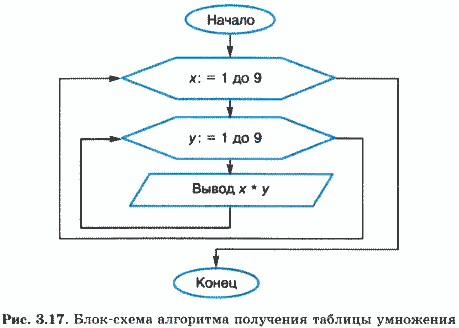
Здесь цикл по параметру у вложен в цикл по параметру х. Последовательность изменения значений параметров циклов такая:
х = 1; у = 1, 2, 3, ..., 9 х = 2; у = 1, 2, 3, ..., 9 ... х = 9; у = 1, 2, 3, ..., 9
Таким образом, внешний цикл исполнится 9 раз, а внутренний — 9 • 9 = 81 раз. На один шаг повторения внешнего цикла происходит полная прокрутка внутреннего.
При программировании вложенных циклов используется понятие глубины вложенности. В данном примере глубина вложенности внутреннего цикла равна единице. Если бы внутри вложенного цикла был еще один вложенный цикл (например, для вычисления всех вариантов перемножения трех сомножителей), то его глубина вложенности равнялась бы двум.
Программа на Паскале получения матрицы Пифагора:

В результате выполнения программы на экране получим:
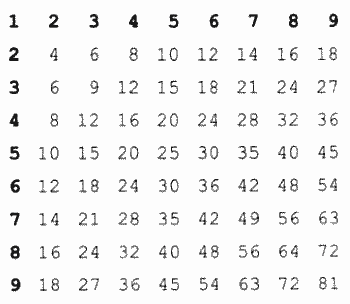
В программе присутствуют некоторые элементы, не отраженные в блок-схеме. В описании переменных X, Y использован ограниченный тип: 1. . 9, поскольку в данной задаче величины принимают целые значения только в этом диапазоне. Оператор WriteLn перед началом вложенного цикла обеспечивает переход к новой строке в таблице каждый раз при смене первого сомножителя. В операторе Write(X*Y:3) для вывода значения произведения после двоеточия использован указатель формата — 3. Это обеспечивает вывод чисел в три позиции на экране, благодаря чему соответствующие столбцы таблицы располагаются строго друг под другом. Первая строка и первый столбец на экране — это сомножители, что соответствует стандартному формату таблицы Пифагора.
Итерационные циклы
 Итерационный цикл — это цикл, для которого число повторений тела цикла заранее неизвестно. В итерационных циклах на каждом шаге вычислений происходят последовательное приближение и проверка условия достижения искомого результата. Выход из итерационного цикла осуществляется в случае выполнения заданного условия.
Итерационный цикл — это цикл, для которого число повторений тела цикла заранее неизвестно. В итерационных циклах на каждом шаге вычислений происходят последовательное приближение и проверка условия достижения искомого результата. Выход из итерационного цикла осуществляется в случае выполнения заданного условия.
 Пример 1. Снова рассмотрим задачу вычисления суммы числового ряда:
Пример 1. Снова рассмотрим задачу вычисления суммы числового ряда:
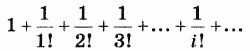
Но теперь условие будет таким: в сумму нужно включить только слагаемые, значение которых больше некоторой малой величины ε. При этом полученная сумма будет отличаться от предельного значения (константы е) на величину, не большую ε.
Поскольку с увеличением значения i величина 1/i! уменьшается, в сумму надо включать все слагаемые, предшествующие первому значению, меньшему ε. Вот две программы решения этой задачи, использующие циклы с предусловием и постусловием:

Решить эту задачу, используя цикл с параметром, нельзя. Итерационные циклы программируются путем использования либо цикла-пока, либо цикла-до.
В качестве результата выводится значение суммы и число вошедших в нее слагаемых. Выполнение этих программ для значения ε=10 -8 дает в результате: Е=2,71828182, Слагаемых: 12. Таким образом, за 12 повторений цикла значение константы е получено с точностью до 8 знаков после запятой. Слово «итерации» означает «приближения». С каждым повторением цикла вычисляемая величина приближалась к предельному значению константы.
 Пример 2. На уроках 33 - 35 "Программирование линейных алгоритмов" была рассмотрена задача вычисления суммы цифр трехзначного натурального числа. Программа имела линейную структуру. Поставим задачу в более общем виде: для любого многозначного натурального числа вычислить сумму всех его цифр.
Пример 2. На уроках 33 - 35 "Программирование линейных алгоритмов" была рассмотрена задача вычисления суммы цифр трехзначного натурального числа. Программа имела линейную структуру. Поставим задачу в более общем виде: для любого многозначного натурального числа вычислить сумму всех его цифр.
Выделение цифр происходит с помощью однотипных действий: использования операций mod и div. Очевидно, что их можно «зациклить». Однако число повторений цикла будет разным для чисел разной длины. Поэтому эта задача не решается с помощью цикла с заданным числом повторений. В таком случае в программе можно использовать либо оператор цикла While, либо Repeat и нельзя — цикл с параметром For.
Программа с использованием цикла с предусловием:

Поскольку при каждом повторении цикла от числа X отбрасывается одна младшая цифра, закончить цикл нужно тогда, когда X станет равным нулю. Обратите внимание на типы переменных. Надо помнить о разнообразии групп типов в Паскале. Назначение переменной X типа Longint дает возможность вводить в нее значения, включающие до десяти знаков. Для переменной Sum, назначен тип Word, поскольку сумма цифр может быть только положительным числом.

Вопросы и задания
1. Найдите все значения натуральных чисел X, Y, Z из интервала от 1 до 10, удовлетворяющих равенству: X2 + Y2 = Z2.
2. Вычислите количество точек с целочисленными координатами, попадающих в круг радиуса R (R > 0) с центром в начале координат.
3. Старинная задача. Сколько можно купить быков, коров и телят на 100 руб., если в сумме должно быть куплено 100 голов скота, а цена быка — 10 руб., цена коровы — 5 руб., цена теленка — 0,5 руб.?
4. Чем отличается итерационный цикл от цикла с заданным числом повторений?
5. Почему для программирования итерационных циклов не используется оператор цикла с параметром?
6. Запрограммируйте итерационный цикл вычисления функции е х (см. задание 9 из "Программирование циклов"*1*) с точностью ε. Сделайте два варианта программы: с циклами While и Repeat. Выполните вычисления для ε = 10 -6, х = 2 и сопоставьте полученный результат со значением стандартной функции ехр (х).
7. Составьте программу определения количества четных и нечетных цифр в записи данного натурального числа.
8. Составьте программу определения наибольшей цифры в записи данного натурального числа.
*1* Задание 9 из "Программирование циклов"
Значение функции е х (экспонента от х) равно сходящейся сумме бесконечного ряда:
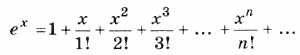
Получите рекуррентную формулу для слагаемых. Используя операторы цикла While, Repeat и For, составьте три варианта программы вычисления суммы с заданным числом слагаемых.
Практикум
Работа 3.4. Программирование циклических алгоритмов
Задание 1
Циклы с заданным числом повторений
Вычислить значение суммы или произведения числовой последовательности.
Уровень 1
1. Дано натуральное число N. Вычислить:
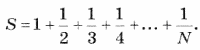
2. Дано натуральное число N. Вычислить:
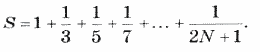
3. Дано натуральное число N. Вычислить:
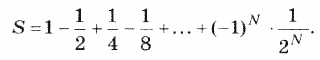
4. Дано натуральное число N. Вычислить:
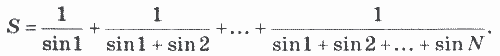
5. Дано натуральное число N. Вычислить произведение первых N сомножителей:
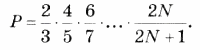
6. Дано натуральное n. Вычислить:
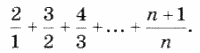
7. Вычислить:
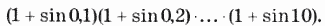
Уровень 2
8. Дано натуральное число N. Вычислить:
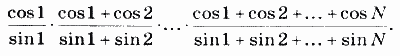
9. Дано действительное число х. Вычислить:
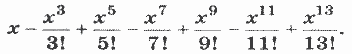
10. Даны натуральное n, действительное х. Вычислить:
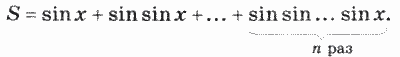
11. Дано действительное х. Вычислить:
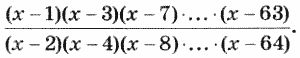
12. Дано натуральное n. Вычислить:
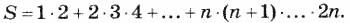
13. Дано натуральное число n. Вычислить:

14. Вычислить по схеме Горнера:
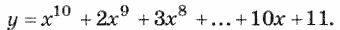
15. Числа Фибоначчи (f n ) определяются формулами
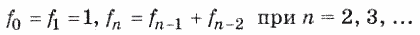
Для данного значения р определить f p .
16. Даны натуральные числа n и k. Вычислить:
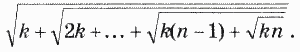
Задание 2
Итерационные циклы
Найти наименьший номер последовательности, заданной рекуррентной формулой, для которого выполняется условие |аn - аn-1| < ε, где ε — малая величина. Вывести на экран этот номер и все элементы ai, где
i = 1, 2, ..., n.
Задание 3
Циклы при обработке целых чисел
Решить поставленные задачи с помощью циклических алгоритмов (простых и вложенных), используя операции целочисленной арифметики.
Уровень 2
1. Натуральные числа а, b, с называются числами Пифагора, если выполняется условие а2 + b2 = с2. Напечатать все числа Пифагора, меньшие N.
2. Найти наибольшую и наименьшую цифры в записи данного натурального числа.
3. Дано натуральное число N. Найти и вывести все числа в интервале от 1 до N - 1, у которых сумма всех цифр совпадает с суммой цифр данного числа. Если таких чисел нет, то вывести слово «нет».
Пример: N = 44. Числа: 17, 26, 35.
4. Дано натуральное число N. Найти и вывести все числа в интервале от 1 до N - 1, у которых произведение всех цифр совпадает с суммой цифр данного числа. Если таких чисел нет, то вывести слово «нет».
Пример: N = 44. Числа: 18, 24.
5. Дано натуральное число N (N > 9). Определить количество нулей, идущих подряд в младших разрядах данного числа.
Пример: N = 1020000. Количество нулей равно четырем.
6. Найти все натуральные числа, не превосходящие заданного n, которые делятся на каждую из своих цифр.
7. Дано натуральное число N. Получить новое число М, которое образуется из числа N путем замены последней цифры на наименьшую цифру в записи числа N.
Пример: N = 128452, М = 128451.
8. Дано натуральное число N. Получить новое число М, которое образуется из числа N путем замены последней цифры на наибольшую цифру в записи числа N.
Пример: N = 128452, М = 128458.
Уровень 3
9. Даны два натуральных числа m и n. Проверить, есть ли в записи числа m цифры, одинаковые с цифрами в записи числа n.
10. Дано натуральное число N (N > 9). Определить количество нулей в цифровой записи числа, кроме нулей в младших разрядах.
Пример: N = 10025000. Количество нулей равно двум.
11. Натуральное число М называется совершенным, если оно равно сумме всех своих делителей, включая 1, но исключая себя. Напечатать все совершенные числа, меньшие заданного числа N.
12. Дано целое n > 2. Напечатать все простые числа из диапазона [2, n].
13. Дано натуральное число N. Определить количество цифр в цифровой записи данного числа, которые имеют наименьшее значение.
Пример: N = 4548. Количество цифр с наименьшим значением равно двум (две цифры 4).
14. Дано натуральное число N. Определить количество цифр в цифровой записи данного числа, которые имеют наибольшее значение.
Пример: N = 1808. Количество цифр с наибольшим значением равно двум (две цифры 8).
15. Палиндром — это сочетания символов, которые читаются одинаково слева направо и справа налево. Например, числа 4884, 121 являются палиндромами. Составить программу, которая определяет, является ли заданное натуральное число палиндромом.
16. Дано натуральное число n. Переставить его цифры так, чтобы образовалось максимальное число, записанное теми же цифрами.
17. Дано натуральное число n. Переставить его цифры так, чтобы образовалось наименьшее число, записанное теми же цифрами.


