Уроки 45 - 47
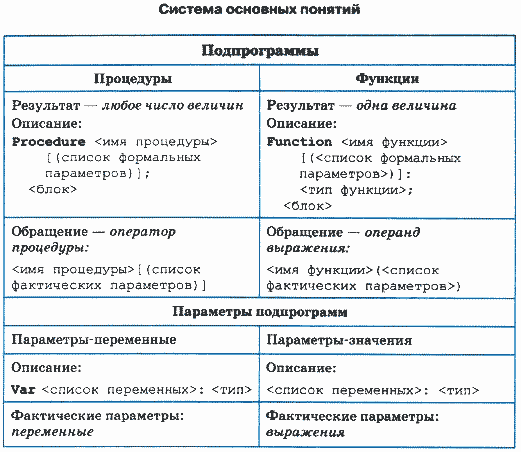
Подпрограммы
Практикум
Практическая работа № 3.5
"Программирование с использованием подпрограмм"

Вспомогательные алгоритмы и подпрограммы

Еще одним важнейшим методологическим приемом структурного программирования является декомпозиция решаемой задачи на подзадачи — более простые, с точки зрения программирования, части исходной задачи. Алгоритмы решения таких подзадач называются вспомогательными алгоритмами.

В языках программирования вспомогательные алгоритмы называются подпрограммами. В Паскале различаются две разновидности подпрограмм: процедуры и функции. Рассмотрим этот вопрос на примере следующей задачи: даны два натуральных числа а и b. Требуется определить наибольший общий делитель трех величин: а + b, а² + b², а • b.

Запишем это так: НОД(а + b, а² + b², а • b).

Идея решения состоит в следующем математическом факте: если х, у, z — три натуральных числа, то НОД(х, y, z) = НОД(НОД(х, у), z). Иначе говоря, нужно найти НОД двух величин, а затем НОД полученного значения и третьего числа (попробуйте это доказать).

Очевидно, что вспомогательным алгоритмом для решения поставленной задачи является алгоритм получения наибольшего общего делителя двух чисел. Эта задача решается с помощью алгоритма Евклида, который подробно обсуждался в 9 классе. Напомним, что идея алгоритма Евклида основана на следующей формуле:

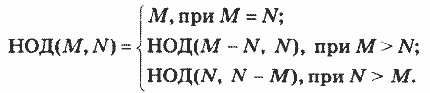
Приведем алгоритм решения поставленной задачи на учебном Алгоритмическом языке. Алгоритм состоит из процедуры «Евклид» и основного алгоритма «Задача», в котором присутствуют два обращения к процедуре:

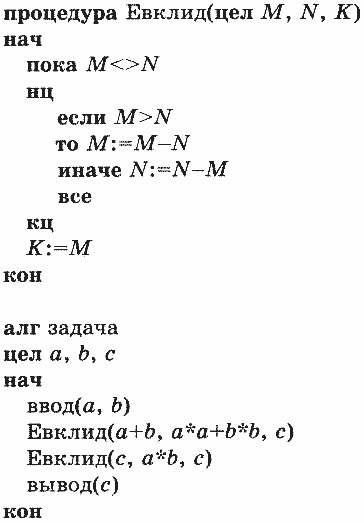
Здесь М, N и К являются формальными параметрами процедуры. М и N — параметры-аргументы, К — параметр-результат.

Процедуры в Паскале. Основное отличие процедур в Паскале от процедур в Алгоритмическом языке (АЯ) состоит в том, что процедуры в Паскале описываются в разделе описания подпрограмм, а в АЯ процедура является внешней по отношению к вызывающей программе. Теперь посмотрим, как решение поставленной задачи программируется на Паскале.

В данном примере обмен аргументами и результатами между основной программой и процедурой производится через параметры. Описание процедуры на Паскале имеет следующий формат:

Procedure <имя процедуры> [(список формальных параметров)]; <блок>

Квадратные скобки указывают на то, что список формальных параметров может отсутствовать, т. е. возможна процедура без параметров. Параметры могут быть параметрами-переменными и параметрами-значениями. Параметры-переменные записываются следующим образом:

Var <список переменных>: <тип>

Параметры-значения указываются так:

<список переменных>: <тип>

Чаще всего аргументы представляются как параметры-значения (хотя могут быть и параметрами-переменными). А для передачи результатов используются параметры-переменные. Процедура в качестве результата может передавать в вызывающую программу множество значений (в частном случае — одно), а может и ни одного. Теперь рассмотрим правила обращения к процедуре. Обращение к процедуре производится в форме оператора процедуры:

<имя процедуры>[(список фактических параметров)]

Если описана процедура с формальными параметрами, то обращение к ней производится оператором процедуры с фактическими параметрами. Правила соответствия между формальными и фактическими параметрами: соответствие по количеству, соответствие по последовательности и соответствие по типам.

Взаимодействие формальных и фактических параметров через параметры-переменные называется передачей по ссылке: при обращении к процедуре ей передается ссылка на переменную, заданную в качестве фактического параметра. Эта ссылка и используется процедурой для доступа к этой переменной.

Другой вариант взаимодействия формальных и фактических параметров называется передачей по значению: вычисляется значение фактического параметра (выражения), и это значение присваивается соответствующему формальному параметру.

В рассмотренном нами примере формальные параметры М и N являются параметрами-значениями. Это аргументы процедуры. При обращении к ней первый раз им соответствуют значения выражений А + В и abs(A - В); второй раз — С и А*В. Параметр К является параметром-переменной. В ней получается результат работы процедуры. В обоих обращениях к процедуре соответствующим фактическим параметром является переменная С. Через эту переменную основная программа получает результат.

Теперь рассмотрим другой вариант программы, решающей ту же задачу. В ней используется процедура без параметров.

Чтобы разобраться в этом примере, требуется объяснить новое для нас понятие: область действия описания.

Областью действия описания любого программного объекта (переменной, типа, константы и т. д.) является тот блок, на который это описание распространяется. Если данный блок вложен в другой (подпрограмма), то присутствующие во вложенном блоке описания являются локальными. Они действуют только в пределах внутреннего блока. Описания же, расположенные во внешнем блоке, называются глобальными по отношению к внутреннему блоку. Если глобально описанный объект используется во внутреннем блоке, то на него распространяется внешнее (глобальное) описание.

В программе NOD1 переменные М, N, К являются локальными внутри процедуры; переменные А, В, С — глобальные. Однако внутри процедуры переменные А, В, С не используются. Связь между внешним блоком и процедурой осуществляется через параметры.

В программе N0D2 все переменные являются глобальными. В процедуре Evklid нет ни одной локальной переменной (нет и параметров). Переменные М и N, используемые в процедуре, получают свои значения через оператор присваивания в основном блоке программы и изменяют значения в подпрограмме. Результат получается в глобальной переменной К, значение которой выводится на экран. Здесь обмен значениями между основной программой и процедурой производится через глобальные переменные.

Использование механизма передачи через параметры делает процедуру более универсальной, независимой от основной программы. Однако в некоторых случаях оказывается удобнее использовать передачу через глобальные переменные. Чаще такое бывает с процедурами, работающими с большими объемами информации. В этой ситуации глобальное взаимодействие экономит память компьютера.

Функции. Теперь выясним, что такое подпрограмма - функция. Обычно функция используется в том случае, когда результатом работы подпрограммы должна быть скалярная (простая) величина. Тип результата называется типом функции. Формат описания функции следующий:

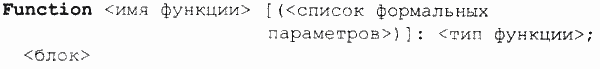
Как и у процедуры, у функции в списке формальных параметров могут присутствовать параметры-переменные и параметры-значения. Всё это — аргументы функции. Параметры вообще могут отсутствовать, если аргументы передаются глобально.

Программа решения рассмотренной выше задачи с использованием функции будет выглядеть следующим образом:

Из примера видно, что тело функции отличается от тела процедуры только тем, что в функции результат присваивается идентификатору функции: Evklid:=M.

Обращение к функции является операндом в выражении. Оно записывается в следующей форме:

<имя функции> (<список фактических лараметров>)

Правила соответствия между формальными и фактическими параметрами все те же. Сравнивая приведенные выше программы, можно сделать вывод, что программа N0D3 имеет определенные преимущества перед другими. Функция позволяет получить результат путем выполнения одного оператора присваивания. Здесь также иллюстрируется возможность того, что фактическим аргументом при обращении к функции может быть эта же функция.

По правилам стандарта Паскаля, возврат в вызывающую программу из подпрограммы происходит, когда выполнение подпрограммы доходит до ее конца (последний End). Однако в современных версиях Паскаля есть средство, позволяющее выйти из подпрограммы в любом ее месте. Это оператор-процедура Exit. Например, функцию определения большего из двух данных вещественных чисел можно описать так:

Модифицированный алгоритм Евклида. Подпрограмму алгоритма Евклида можно составить иначе, если воспользоваться операцией mod (получение остатка от деления), имеющейся в Паскале. Идея алгоритма исходит из справедливости следующих равенств:

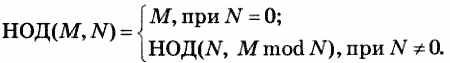
В таком случае функцию Evklid можно переписать так:

Вопросы и задания

1. Для чего используются подпрограммы?

2. В чем различие между процедурами и функциями?

3. Какие существуют способы передачи данных между подпрограммой и вызывающей ее программой?

4. Составьте программу вычисления площади кольца по значениям внутреннего и внешнего радиусов, используя подпрограмму вычисления площади круга (два варианта: с процедурой и с функцией).

5. Составьте программу сложения двух простых дробей. Результат должен быть несократимой дробью. Используйте подпрограмму вычисления НОД по алгоритму Евклида. Простая дробь задается двумя целыми числами: числителем и знаменателем.

6. По координатам вершин треугольника вычислите его периметр, используя подпрограмму вычисления длины отрезка между двумя точками.

7. Даны три целых числа. Определите, у которого из них больше сумма цифр. Подсчет суммы цифр организуйте через подпрограмму.

---

Практикум

Работа 3.5. Программирование с использованием подпрограмм

Задание 1

Для решения всех задач сделать два варианта программы: с реализацией указанной подпрограммы в виде функции и в виде процедуры.

Уровень 1

1. Составить программу нахождения наибольшего общего делителя (НОД) и наименьшего общего кратного (НОК) двух натуральных чисел

.

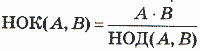Использовать подпрограмму алгоритма Евклида для определения НОД.

2. Вычислить площадь правильного шестиугольника со стороной а, используя подпрограмму вычисления площади треугольника.

3. Даны две дроби 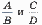— (А, В, С, D — натуральные числа).

Составить программу деления дроби на дробь. Ответ должен быть несократимой дробью. Использовать подпрограмму алгоритма Евклида для определения НОД.

4. Даны две дроби 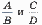— (А, В, С, D — натуральные числа).

Составить программу умножения дроби на дробь. Ответ должен быть несократимой дробью. Использовать подпрограмму алгоритма Евклида для определения НОД.

5. Даны две дроби 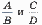— (А, В, С, D — натуральные числа).

Составить программу вычитания из первой дроби второй. Ответ должен быть несократимой дробью. Использовать подпрограмму алгоритма Евклида для определения НОД.

6. Написать программу вычисления суммы 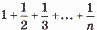— для заданного числа n. Результат представить в виде несократимой дроби 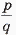(р, q — натуральные). Использовать подпрограммы алгоритма Евклида для определения НОД и сложения двух простых дробей.

7. Даны числа X, Y, Z, Т — длины сторон четырехугольника. Вычислить его площадь, если угол между сторонами длиной X и Y — прямой. Использовать две подпрограммы для вычисления площадей: прямоугольного треугольника и прямоугольника.

Задание 2

Для всех задач выделить подзадачи, решения которых могут быть реализованы через подпрограммы. Выбрать наиболее удобный вариант подпрограммы: функцию или процедуру. Составить программу решения задачи.

Уровень 2

1. Дано простое число. Найти следующее за ним простое число.

2. Для заданного натурального числа п найти наименьший нечетный натуральный делитель k (k ≠ 1).

3. Заменить данное натуральное число на число, которое получается из исходного записью его цифр в обратном порядке (например, дано число 156, нужно получить 651).

4. Найти все натуральные числа, не превосходящие заданного п, которые делятся на каждую из своих цифр.

5. Имеется часть катушки с автобусными билетами. Номер билета шестизначный. Составить программу, определяющую количество счастливых билетов на катушке, если меньший номер билета — N, больший — М (билет является счастливым, если сумма первых трех его цифр равна сумме последних трех).

6. Из заданного числа вычли сумму его цифр. Из результата вновь вычли сумму его цифр и т. д. Через сколько таких действий получится нуль?

7. На отрезке [100, А] (2¹⁰ < N < 2³¹) найти количество чисел, составленных из цифр а, b, с.

8. Найти все натуральные n-значные числа, цифры в которых образуют строго возрастающую последовательность (например, 1234,5789).

Уровень 3

9. Два простых числа называются «близнецами», если они отличаются друг от друга на 2 (например, 41 и 43). Напечатать все пары «близнецов» из отрезка [n, 2n], где n — заданное натуральное число, большее 2.

10. Дано четное число n > 2. Проверить для него гипотезу Гольдбаха: каждое четное п представляется в виде суммы двух простых чисел.

11. Составить программу разложения данного натурального числа на простые множители. Например, 200 = 2³ • 5².

12. Дано натуральное число n. Найти все меньшие п числа Мерсенна. (Простое число называется числом Мерсенна, если оно может быть представлено в виде 2^p — 1, где р — тоже простое число. Например, 31 = 2⁵ - 1 — число Мерсенна.)

13. Два натуральных числа называются «дружественными», если каждое из них равно сумме всех делителей (кроме его самого) другого (например, числа 220 и 284). Найти все пары «дружественных» чисел, которые не больше данного числа N.

14. Натуральное число, в записи которого n цифр, называется числом Армстронга, если сумма его цифр, возведенная в степень n, равна самому числу. Найти все числа Армстронга от 1 до k.

15. Найти все простые натуральные числа, не превосходящие n, двоичная запись которых представляет собой палиндром, т. е. читается одинаково слева направо и справа налево.

16. Составить программу для нахождения чисел из интервала [М, N], имеющих наибольшее количество делителей.

17 Дано натуральное число n > 1. Определить длину периода десятичной записи дроби 1/n.