Уроки 48 - 54
Работа с массивами
Практикум
Практическая работа № 3.6
"Программирование обработки одномерных массивов"
Практическая работа № 3.7
"Программирование обработки двумерных массивов"

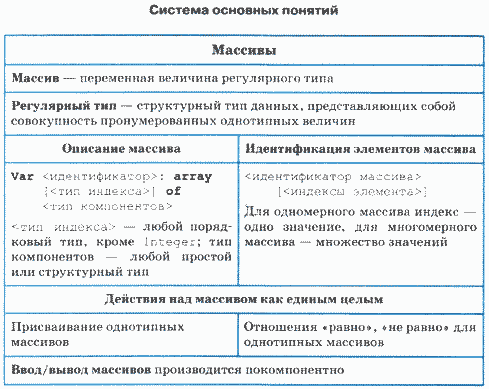
Массивы

Массивом в Паскале называют переменную величину регулярного типа.

Регулярный тип — это структурный тип данных, представляющих собой совокупность пронумерованных однотипных величин.

Описание массивов. Переменная регулярного типа описывается в разделе описания переменных в следующей форме:

Var <идентификатор>: array[<тип индекса>] of <тип компонентов>

В данном случае квадратные скобки — это обязательные символы, которые называются индексными скобками. Чаще всего в качестве типа индекса употребляется ограниченный тип. Например, массив вещественных чисел, хранящий 12 значений среднемесячных температур в течение года, опишется так:

Var Т: array[1..12] of Real;

Описание массива определяет, во-первых, размещение массива в памяти, во-вторых, правила его дальнейшего употребления в программе.

Элемент массива идентифицируется в виде переменной с индексами:

<Идентификатор массива> [<Индексы элемента>]

Для одномерного массива индекс — это одно значение. Для многомерных массивов индекс — множество значений. В качестве индекса может употребляться любое выражение соответствующего типа. Например, для элементов массива температур возможны обозначения: Т[5] , Т[k], T[i + j], T[m div 2].

Последовательные элементы массива располагаются в последовательных ячейках памяти (Т [1], Т[2] и т. д.), причем значения индекса не должны выходить за диапазон 1. .12.

Тип индекса может быть любым скалярным порядковым типом, кроме Integer. Например, в программе могут присутствовать следующие описания:

Var cod: array[Char] of 1..100; L: array[Boolean] of Char;

В такой программе допустимы следующие обозначения элементов массивов:

cod['x']; Lftrue]; cod[chr(65) ] ; L[a>0].

В некоторых случаях бывает удобно в качестве индекса использовать перечислимый тип. Например, данные о количестве учеников в четырех десятых классах одной школы могут храниться в следующем массиве:

Type Index = (А, В, С, D) ;

Var class_10: array[Index] of Byte;

И если, например, элемент class 10 [А] равен 35, то это означает, что в 10А классе 35 человек. Такое индексирование улучшает наглядность программы.

Часто структурному типу присваивается имя в разделе типов, которое затем используется в разделе описания переменных.

Type Masl = array [1..100] of Integer;

Mas2 = array [-10.. 10] of Char;

Var Num: Masl; Sim: Mas2;

До сих пор речь шла об одномерных массивах, в которых типы элементов скалярные.

Многомерный массив в Паскале трактуется как одномерный массив, тип элементов которого также является массивом (массив массивов).

В качестве примера рассмотрим таблицу с информацией о среднемесячных температурах за 10 лет, например с 2001 по 2010 год. Очевидно, для этого удобна прямоугольная (двумерная) таблица, в которой столбцы соответствуют месяцам, а строки — годам.

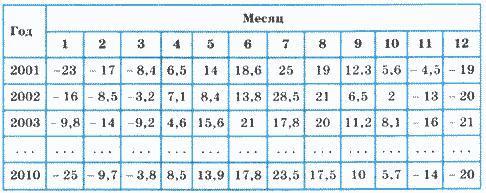
Для обработки такой таблицы в программе следует описать массив:

Var Тabl: array[2001..2010] of array[1.. 12] of Real;

Вот примеры обозначения некоторых элементов этого массива:

Тabl [2001] [1] ; Тabl [2005] [10] ; Тabl [2010] [12] .

Однако чаще употребляется другая, эквивалентная форма обозначения элементов двумерного массива:

Тabl [2 001, 1] ; Тabl [2005, 10] ; Тabl [2010,12] .

Переменная ТаЫ [2 001] обозначает всю первую строку таблицы, т. е. весь массив температур за 2001 год. Другим эквивалентным вариантом приведенному выше описанию является следующее:

Туре Month = array [1..12] of Real;

Year = array [2001..2010] of Month;

Var Tabl: Year;

Наиболее краткий вариант описания данного массива такой:

Var Tabl: array [2001.. 2010, 1..12] of Real;

Продолжая по аналогии, можно определить трехмерный массив как одномерный массив, у которого элементами являются двумерные массивы. Вот пример описания трехмерного массива:

Var A: array[1..10, 1..20, 1..30] of Integer;

Это массив, состоящий из 10 • 20 • 30 = 6000 целых чисел и занимающий в памяти 6000 • 2 = 12 000 байтов. В Паскале нет ограничения сверху на размерность массива. Однако в каждой конкретной реализации Паскаля ограничивается объем памяти, выделяемый под массивы. В Турбо Паскале это ограничение равно 64 килобайтам.

По аналогии с математикой одномерные числовые массивы часто называют векторами, а двумерные — матрицами.

В Паскале не допускается употребление динамических массивов, т. е. таких, размер которых определяется в процессе выполнения. Изменение размеров массива происходит через изменение в тексте программы и повторную компиляцию. Для упрощения таких изменений удобно определять индексные параметры в разделе констант:

Const Imax = 10; Jmax = 20;

Var Mas: array[1..Imax, l..Jmax] of Integer;

Теперь для изменения размеров массива Mas и всех операторов программы, связанных с этими размерами, достаточно отредактировать только одну строку в программе — раздел констант.

Действия над массивом как единым целым. Такие действия допустимы лишь в двух случаях:

• присваивание значений одного массива другому;
• применение к массивам операций отношения «равно», «не равно».

В обоих случаях массивы должны иметь одинаковые типы (тип индексов и тип элементов).

Пример 1

Var Р, Q: array [1.. 5, 1..10] of Real;

При выполнении операции присваивания

P:=Q

все элементы массива Р станут равными соответствующим элементам массива Q.

Пример 2

Как уже отмечалось, в многомерных массивах переменная с индексом может обозначать целый массив. Тогда если массив ТаЫ описан так:

Type mas = array [1..12] of Real;

Var Таbl: array [2001.. 2010] of mas;

и в нем требуется данные за 2009 год сделать такими же, как за 2001 год (девятой строке присвоить значение первой строки), то это можно сделать одним присваиванием:

Таbl [2009] : =Таbl [2001]

А если нужно поменять местами значения этих строк, то это делается через третью переменную того же типа:

Р:=Таbl [2009] ; Таbl [2009] : =Таbl [2001 ] ; Таbl [2001] :=Р; где Р описана так:

Var Р: mas;

Ввод и вывод массивов производятся покомпонентно. Вот примеры ввода с клавиатуры значений одномерного и двумерного массивов:

For I: =1 То 12 Do

ReadLn(Т[I]);

For I:=l To Imax Do

For J:=l To Jmax Do

ReadLn(Mas[I, J]);

Здесь каждое следующее значение будет вводиться с новой строки. Для построчного ввода используется оператор Read.

Аналогично в цикле по индексной переменной организуется вывод значений массива на экран. Например:

For I: =1 То 12 Do Write (Т [ I ] : 8 : 4 ) ;

Напомним, что модификатор формата 8:4 означает вывод числа в формате с фиксированной точкой в 8 позициях, из которых в 4 последних позициях размещается дробная часть.

Следующий фрагмент программы организует построчный вывод матрицы на экран:

После вывода очередной строки матрицы оператор Writeln без параметров переведет курсор в начало новой строки. Следует заметить, что в последнем примере матрица на экране будет получена в естественной форме прямоугольной таблицы, если Jmax не превышает 12 (подумайте почему).

Вопросы и задания

1. Что такое регулярный тип данных? Что такое массив?

2. Какие типы допустимы для индексов массива?

3. Как в Паскале трактуется многомерный массив?

4. Какие действия можно выполнять над массивом как единым целым?

5. Дан вектор {z}, i = 1, …, 50. Составьте программу ввода значений и вычисления длины этого вектора по следующей формуле:

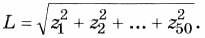
6. Даны значения массива {а_i}, i = 0, ..., 10 и переменной х. Составьте программу вычисления алгебраического многочлена 10-й степени по формуле Горнера:

a₁₀x¹⁰ + а₉х⁹ + ... + а₁х + а₀ = ((...(а₁₀х + а₉)х + а₈)х + ... + а₁)х + а₀.

Типовые задачи обработки массивов

Заполнение массива

Значения массива могут задаваться вводом с клавиатуры, чтением из файла или вычислением в программе. В некоторых задачах статистического характера требуется заполнять массивы случайными числами.

Пример 1. Заполнить массив равномерно распределенными целыми случайными числами в диапазоне от 0 до 100.

Со стандартной функцией Random (х) вы уже знакомы. Напомним, что она возвращает псевдослучайное целое число в диапазоне от 0 до х - 1.

Если требуется изменить диапазон случайных чисел, то это всегда можно сделать путем сдвига. Например, если нужно получить числа в диапазоне от -50 до 50, то в программе пишется оператор присваивания:

X[i]:=Random(100)-50;

Для получения вещественных случайных чисел используется функция Random без аргумента. Она возвращает случайные дробные значения в диапазоне [0,1). С помощью сдвига и множителя эти значения можно привести к любому диапазону. Например, следующее выражение будет вычислять случайное вещественное число в диапазоне значений от -5 до 5: 10 * Random-5.

Пример 2. Заполнить верхнетреугольную матрицу указанного вида и вывести ее на экран.

Пояснение: для элементов M[i, j] матрицы М, расположенных в верхнем треугольнике (включая диагональ), выполняется следующее соотношение между индексами: j ≤ i.

Пример 3. Выбор максимального элемента. В одномерном массиве X из примера 1 требуется определить наибольшее значение среди значений элементов и его порядковый номер (индекс).

Идея алгоритма решения этой задачи следующая: чтобы в переменной ХМах получить максимальное значение массива X, сначала в нее заносится первое значение массива Х[1]. Затем значение ХМах поочередно сравнивается с остальными элементами массива, и каждое значение, большее Хmах, присваивается этой переменной. Для получения номера максимального элемента массива в целочисленной переменной imax следует записывать в нее номер элемента массива X одновременно с занесением значения в Хmах. На Алгоритмическом языке это запишется так:

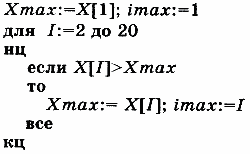
Заметим, что если в массиве X несколько значений, равных максимальному, то в imax будет получен первый номер из этих элементов. Чтобы получить номер последнего элемента, равного максимальному, нужно в ветвлении если заменить знак отношения > на >=. Для нахождение минимального элемента массива достаточно заменить знак отношения «больше» на «меньше».

Оформим в виде процедуры на Паскале подпрограмму поиска максимального элемента в одномерном массиве. Заполним одномерный массив случайными числами (как в примере 1). С помощью процедуры найдем в нем максимальное значение и индекс его первого вхождения в массив.

Процедура МахАггау имеет три параметра: исходный массив А, Мах А — переменную для найденного максимального значения, k — переменную для индекса максимального значения. При обращении к процедуре им соответствуют фактические параметры: X, Xmax, imax. Размер массива определяется глобальной константой n, значение которой используется как в основной программе, так и в процедуре.

Пример 4. Сортировка массива. В одномерном массиве X из N элементов требуется произвести перестановку значений так, чтобы они расположились по возрастанию, т. е. Х₁ ≤ Х₂ ≤ ... ≤ X_N.

Существует целый класс алгоритмов сортировки. Ниже описан алгоритм, который называется методом пузырька.

Идея алгоритма: производится последовательное упорядочивание смежных пар элементов массива: Х₁ и Х₂, Х₂ и Х₃,..., X_N-1 и X_N. В итоге максимальное значение переместится в X_N. Затем ту же процедуру повторяют до Х_N-1 и т. д., вплоть до цепочки из двух элементов Х₁ и Х₂. Такой алгоритм будет иметь структуру двух вложенных циклов, причем внутренний цикл переменной (сокращающейся) длины.

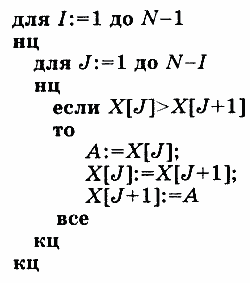
Для сортировки массива по убыванию значений достаточно заменить знак отношения «больше» на «меньше».

Запрограммируем на Паскале процедуру сортировки массива по возрастанию методом пузырька.

Пример 5. Ранее было рассмотрено описание двумерного массива, содержащего среднемесячные температуры за 10 лет, с 2001 по 2010 год. Определить, в каком году за этот период было самое теплое лето, т. е. в каком году была наибольшая средняя температура летних месяцев.

Идея решения: в одномерном массиве S получить средние температуры летних месяцев за каждый год из 10 лет. Затем найти номер наибольшего элемента в этом массиве, это и будет искомый год.

Вопросы и задания

1. Какими способами можно заполнить массив значениями?

2. Как можно вычислять целые случайные числа в диапазоне от -50 до 0?

3. Как можно вычислять вещественные случайные числа в диапазоне от 2,5 до 10?

4. Даны два вектора{х_i}, {y_i}, i = 1, ..., 10, упорядоченные по возрастанию. Соедините их в один вектор {z_i}, i = 1, ..., 20 так, чтобы сохранилась упорядоченность.

5. Дан массив, состоящий из 100 целых чисел. Выведите все числа, которые встречаются в этом массиве:

а) несколько раз;
б) только по одному разу.

6. В целочисленной матрице размером 10 х 10 найдите максимальное значение и индексы всех элементов, равных ему.

7. Матрицу размером 5 х 10 заполните случайными двоичными цифрами (0 и 1). Определите номер строки с наибольшим количеством нулей.

8. В двоичной матрице размером 10 х 10 (см. задание 7) найдите совпадающие строки.

---

Практикум

Работа 3.6. Программирование обработки одномерных массивов

Задание

Составить программу решения поставленной задачи по обработке одномерного массива (вектора). По возможности, использовать подпрограммы.

Уровень 1

1. Дана последовательность действительных чисел а₁, а₂, …, а_n. Выяснить, будет ли она возрастающей.

2. Дан массив из N действительных чисел. Подсчитать, сколько в нем отрицательных, положительных и нулевых элементов.

3. Даны действительные числа а₁, а₂, …, а_n. Поменять местами первый наибольший элемент с последним наименьшим элементом.

4. В заданном одномерном массиве поменять местами соседние элементы, стоящие на четных местах, с элементами, стоящими на нечетных местах.

5. Задана последовательность {X_i} из N вещественных чисел. Вычислить последовательность {S_i} по формуле:

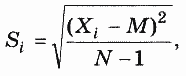
где М — среднее арифметическое значение последовательности X.

6. Задана последовательность из N целых чисел. Вычислить сумму тех элементов массива, порядковые номера которых совпадают со значением этого элемента.

7. Определить, сколько процентов от всего количества элементов последовательности целых чисел составляют нечетные элементы.

8. Дан массив Х_[N] целых чисел. Не используя других массивов, переставить его элементы в обратном порядке. 9. Задана последовательность из N вещественных чисел. Вычислить сумму чисел, порядковые номера которых являются простыми числами.

10. Последовательность а₁, а₂, …, а_2n состоит из нулей и единиц. Поместить в начало этой последовательности все нули, а затем все единицы.

11. Даны действительные числа а₁, а₂, …, а_2n. Найти:

mах(a₁ + а_2n, а₂ +а_2n-1, …, а_n + а_n+1).

12. Дана последовательность действительных чисел a₁ ≤ а₂ ≤ ... ≤ а_n. Вставить действительное число b в нее так, чтобы последовательность осталась неубывающей.

13. Дана последовательность целых чисел а₁, а₂, …, а_n. Указать пары чисел а_i, а_j, таких что a_i + а_j = m, где m - заданное целое число.

14. Даны координаты n (n ≤ 30) точек на плоскости: (Х₁, У₁), ..., (Х_п, Y_n). Найти номера пары точек, расстояние между которыми наибольшее (считать, что такая пара единственная).

15. Дан массив, состоящий из n натуральных чисел. Образовать новый массив, элементами которого будут элементы исходного, оканчивающиеся на цифру k.

16. Дан массив целых чисел. Найти в этом массиве минимальный элемент m и максимальный элемент М. Получить в порядке возрастания все целые числа из интервала (m; М), которые не входят в данный массив.

17. Даны две последовательности а₁, а₂, ..., а_n и b_х, b₂, ..., b_n (m < п). В каждой из них значения элементов различны. Верно ли, что все элементы второй последовательности входят в первую последовательность?

18. Вывести значения и номера наибольшего, наименьшего и наименее удаленного от среднего арифметического значения элементов данной последовательности вещественных чисел.

Уровень 3

19. Сформировать массив простых чисел, не больших заданного натурального числа N.

20. Сформировать массив простых множителей заданного числа.

21. В одномерном массиве все отрицательные элементы переместить в начало массива, а остальные — в конец с сохранением порядка следования. Дополнительный массив заводить не разрешается.

22. В одномерном массиве с четным количеством элементов (2N) находятся координаты N точек плоскости. Они располагаются в следующем порядке: х₁, у₁, х₂, у₂, х₃, у₃, и т. д. Определить:

а) минимальный радиус окружности с центром в начале координат, которая содержит все точки;
б) внутренний и внешний радиусы кольца с центром в начале координат, которое содержит все точки;
в) номера точек, которые могут являться вершинами квадрата;
г) номера точек, которые могут являться вершинами равнобедренного треугольника;
д) номера самых удаленных и наименее удаленных друг от друга точек;
е) три точки, которые являются вершинами треугольника, для которого разность точек вне его и внутри является минимальной.

23. Дана последовательность целых чисел. Найти количество различных чисел в этой последовательности.

24. На плоскости п точек заданы своими координатами, и также дана окружность радиуса R с центром в начале координат. Указать множество всех треугольников с вершинами в заданных точках, пересекающихся с окружностью; множество всех треугольников, содержащихся внутри окружности.

25. Разделить массив на две части, поместив в первую элементы, большие среднего арифметического элементов массива, а во вторую — меньшие (части не сортировать).

26. Даны две последовательности а₁ < а₂ < ... < а_n и b₁ < b₂ < ... < b_m. Образовать из них новую последовательность чисел так, чтобы она тоже была неубывающей.

Примечание. Дополнительный массив не использовать.

27. Сортировка вставками. Дана последовательность чисел а₁, а₂, ..., а_n. Требуется переставить числа в порядке возрастания. Делается это следующим образом. Пусть а₁, а₂, ..., a_i — упорядоченная по неубыванию последовательность, т. е. а₁ < а₂ < ... < а_i. Берется следующее число a_i+1 и вставляется в последовательность так, чтобы новая последовательность была также возрастающей. Процесс производится до тех пор, пока все элементы от i+1 до n не будут перебраны.

Примечание. Место помещения очередного элемента в отсортированную часть найти с помощью двоичного поиска. Двоичный поиск оформить в виде отдельной функции.

28. Алгоритм сортировки фон Неймана. Упорядочить массив а₁, а₂, ..., а_n по неубыванию с помощью алгоритма сортировки слияниями:

1) каждая пара соседних элементов сливается в одну группу из двух элементов (последняя группа может состоять из одного элемента);

2) каждая пара соседних двухэлементных групп сливается в одну четырехэлементную группу и т. д.

При каждом слиянии новая укрупненная группа упорядочивается.

29. Шейкер-сортировка. Алгоритм «пузырьковой» сортировки легко улучшить. Разумно запомнить, производился ли на данном проходе какой-либо обмен. Если нет, то алгоритм можно закончить. Еще одно улучшение заключается в том, что периодически меняется направление сортировки, которое борется с некоторой асимметрией «пузырькового» метода. Написать программу, реализующую данный улучшенный алгоритм.

Работа 3.7. Программирование обработки двумерных массивов

Задание

Составить программу решения поставленной задачи по обработке двумерного массива (матрицы). По возможности, использовать подпрограммы.

Уровень 1

1. Вычислить сумму и число положительных элементов матрицы A[N, N], находящихся над главной диагональю.

2. Дана целая квадратная матрица n-го порядка. Определить, является ли она магическим квадратом, т. е. такой матрицей, в которой суммы элементов во всех строках и столбцах одинаковы.

3. Определить, является ли заданная целая квадратная матрица n-го порядка симметричной (относительно главной диагонали).

4. Дана целочисленная квадратная матрица. Найти в каждой строке наибольший элемент и поменять его местами с элементом главной диагонали в этой же строке.

5. Упорядочить по возрастанию элементы каждой строки матрицы размером n х m.

6. Задана квадратная матрица. Получить транспонированную матрицу (перевернутую относительно главной диагонали).

7. Квадратная матрица, симметричная относительно главной диагонали, задана верхним треугольником в виде одномерного массива. Восстановить исходную матрицу и напечатать по строкам.

8. Задана матрица порядка n и число k. Разделить элементы k-й строки на диагональный элемент, расположенный в этой строке.

9. Для целочисленной квадратной матрицы найти число элементов, кратных k, и наибольший из этих элементов.

10. Найти наибольший и наименьший элементы прямоугольной матрицы и поменять их местами.

11. В данной действительной квадратной матрице порядка п найти сумму элементов строки, в которой расположен элемент с наименьшим значением. Предполагается, что такой элемент единственный.

12. Дана действительная матрица размером n х m. Требуется преобразовать матрицу: поэлементно вычесть последнюю строку из всех строк, кроме последней.

13. Определить наименьший элемент каждой четной строки матрицы А[М, N].

Уровень 2

14. Задана квадратная матрица. Переставить строку с максимальным элементом на главной диагонали со строкой с заданным номером m.

15. Определить номера строк матрицы R[M, N], хотя бы один элемент которых равен с, и элементы этих строк умножить на d.

16. Дана матрица B[N, М]. Найти в каждой строке матрицы максимальный и минимальный элементы и поменять их с первым и последним элементами строки соответственно.

17. Элемент матрицы назовем седловой точкой, если он является наименьшим в своей строке и одновременно наибольшим в своем столбце или, наоборот, является наибольшим в своей строке и наименьшим в своем столбце. Для заданной целой матрицы размером n х m напечатать индексы всех ее седловых точек.

18. Дана вещественная матрица размером n х m. Переставляя ее строки и столбцы, добиться того, чтобы наибольший элемент (или один из них) оказался в верхнем левом углу.

19. Дана квадратная матрица A[N, А]. Записать на место отрицательных элементов матрицы нули, а на место положительных — единицы. Вывести на печать нижнюю треугольную матрицу в общепринятом виде.

20. Дана действительная матрица размером n х m, все элементы которой различны. В каждой строке выбирается элемент с наименьшим значением, затем среди этих чисел выбирается наибольшее. Указать индексы элемента с найденным значением.

21. Дана действительная квадратная матрица порядка N (N — нечетное), все элементы которой различны. Найти наибольший элемент среди стоящих на главной и побочной диагоналях и поменять его местами с элементом, стоящим на пересечении этих диагоналей.

22. Для заданной квадратной матрицы сформировать одномерный массив из ее диагональных элементов. Найти след матрицы, просуммировав элементы одномерного массива. Преобразовать исходную матрицу по правилу: четные строки разделить на полученное значение, нечетные оставить без изменения.

23. Дана прямоугольная матрица. Найти строку с наибольшей и строку с наименьшей суммой элементов. Вывести на печать найденные строки и суммы их элементов.

24. В данной действительной квадратной матрице порядка п найти наибольший по модулю элемент. Получить квадратную матрицу порядка n - 1 путем отбрасывания из исходной матрицы строки и столбца, на пересечении которых расположен элемент с найденным значением.

25. Расположить столбцы матрицы D[M, N] в порядке возрастания элементов k-й строки (1 ≤ k ≤ М).

Уровень 3

26. Среди столбцов заданной целочисленной матрицы, содержащих только такие элементы, которые по модулю не больше 10, найти столбец с минимальным произведением элементов.

27. Для заданной квадратной матрицы найти такие k, что k-я строка матрицы совпадает с k-м столбцом.

28. Найти максимальный среди всех элементов тех строк заданной матрицы, которые упорядочены (либо по возрастанию, либо по убыванию).

29. Составить программу, которая заполняет квадратную матрицу порядка п натуральными числами 1, 2, 3, ..., n², записывая их в нее «по спирали».

Например, для n = 5 получаем следующую матрицу:

30. Среди тех строк целочисленной матрицы, которые содержат только нечетные элементы, найти строку с максимальной суммой модулей элементов.

31. Подсчитать количество строк заданной целочисленной матрицы N х N, являющихся перестановкой чисел 1, 2, ..., N (т. е. содержащих каждое из чисел 1, 2, ..., N ровно один раз).