Уроки 55 - 57
Организация ввода - вывода с использованием файлов
Практикум
Практическая работа № 3.6
"Программирование обработки одномерных массивов"
Практическая работа № 3.7
"Программирование обработки двумерных массивов"

До сих пор мы программировали ввод исходных данных с клавиатуры и вывод на экран монитора.

Вводом/выводом называется обмен данными между оперативной памятью и любыми внешними устройствами, в том числе устройствами внешней памяти: магнитными и оптическими дисками, флеш-накопителями.

Информация на внешних носителях хранится в файлах. По форме хранения данных файлы бывают типизированными, нетипизированными и текстовыми. В типизированных и нетипизированных файлах данные различных типов хранятся в том же формате, что и в оперативной памяти. Следовательно, при чтении и записи в такие файлы данные копируются, не изменяя объема и формы своего представления. В текстовых файлах данные хранятся в символьном формате. Поэтому при вводе (чтении) чисел из текстового файла происходит преобразование их представления из символьной формы в форму их внутреннего представления (с фиксированной или плавающей запятой). А при выводе (записи) чисел в текстовый файл они преобразуются из внутренней формы в символьную.

Далее мы будем использовать только текстовые файлы.

Текстовые файлы

Текстовый файл — наиболее часто употребляемая разновидность файлов. Устройства ввода с клавиатуры и вывода на экран работают только с текстовыми файлами. Файлы, содержащие тексты программ на Паскале и других языках программирования, являются текстовыми. Различная документация, информация, передаваемая по каналам электронной связи, — всё это текстовые файлы.

Содержимое текстового файла представляет собой символьную последовательность, разделенную на строки. Каждая строка заканчивается специальным признаком EOLN {end of line — конец строки). Весь файл заканчивается признаком EOF {end of file — конец файла). Схематически это выглядит так:

Здесь S, обозначает i-й символ в строке. Каждый символ представлен во внутреннем коде (ASCII) и занимает 1 байт. Признак EOLN состоит из двух однобайтовых управляющих кодов: CR (код ASCII — 13) — возврат к началу строки и LF (код ASCII — 10) — перевод строки. При выводе содержимого текстового файла на экран или на печать признак EOLN обеспечивает визуальное разделение строк: переход к продолжению вывода с новой строки.

Текстовый файл можно создать или преобразовать с помощью текстового редактора. Его можно просмотреть на экране монитора или распечатать на принтере.

Ввод из текстового файла

Исходные данные могут быть заранее подготовлены в файле с помощью текстового редактора и сохранены на диске под определенным именем. Ввод исходных данных из файла производится автоматически, и при этом не происходит задержки выполнения программы, как при клавиатурном вводе.

Для организации ввода данных из текстового файла следует:

• объявить в программе переменную с типом Text (она называется файловой переменной);
• связать файловую переменную с файлом внешней памяти, содержащим исходные данные, с помощью оператора Assign;
• открыть файл для чтения с помощью процедуры Reset;
• осуществить чтение из файла с помощью операторов Read или ReadLn;
• закрыть файл с помощью оператора Close.

Пример 1. В текстовом файле с именем abc.txt хранятся пять чисел, разделенных на две строки:

2.5  3.1  4.0

0.7  1.5

В следующей программе организован ввод этих данных в вещественные переменные а, b, с, d, е.

Если файл хранится не в текущем каталоге, то в операторе Assign кроме имени файла надо указывать полный путь к нему. Имя файла можно задавать в строковой константе или переменной.

Для массивов большого размера удобно производить ввод значений из заранее подготовленного текстового файла с исходными данными.

Пример 2. Пусть в текстовом файле с именем matr.txt с помощью текстового редактора записана следующая числовая матрица размером 4x4:

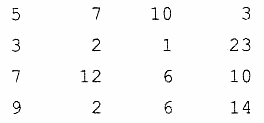
В следующей программе производится ввод этой матрицы в двумерный массив М:

Вывод в текстовый файл

Запись результатов выполнения программы в текстовый файл позволяет сохранить их для того, чтобы в дальнейшем можно было их просмотреть с помощью текстового редактора, распечатать на принтере, а также использовать в качестве исходных данных для другой программы.

Для организации вывода данных в текстовый файл следует:

• объявить в программе файловую переменную с типом Text;
• связать файловую переменную с файлом внешней памяти с помощью оператора Assign;
• открыть файл для записи с помощью процедуры Rewrite;
• осуществить запись в файл с помощью операторов Write или WriteLn;
• закрыть файл с помощью оператора Close.

Пример 3. Требуется записать в текстовый файл таблицу умножения на 2.

Var A: Integer;

ТМ: Text; {Описание файловой переменной}

Begin

Assign (ТМ, 'E:\TabMul.txt'); {Связывание переменной ТМ с файлом}

Rewrite(ТМ); {Открытие файла для записи} {Циклический вывод в файл таблицы умножения}

For А:=2 То 9 Do WriteLn(ТМ, 2, '*', А, '=', 2*А) ;

Close(ТМ) {Закрытие файла}

End.

Процедуры открытия файла для записи и запись в файл имеют следующий формат:

Rewrite(<файловая переменная>)

Write(<файловая переменная>, <список вывода>)

WriteLn(<файловая переменная>, <список вывода>)

Если файла с именем, указанным в операторе Assign, на диске не было, то программа его создаст. Если такой файл уже был, то его прежнее содержание будет утеряно и в него запишутся новые данные. В конце выполнения оператора WriteLn выставляется признак EOLN. Оператор Write этого не делает. Закрытие файла приводит к выставлению признака EOF.

В результате выполнения программы в корневом каталоге диска Е появится файл с именем TabMul.txt. Открыв его в текстовом редакторе, увидим:

2*2 = 4
2*3 = 6
2*4 = 8
2*5 = 10
2*6 = 12
2*7 = 14
2*8 = 16
2*9 = 18

Вопросы и задания

1. Сформулируйте правила организации ввода данных из текстового файла.

2. Сформулируйте правила организации вывода данных в текстовый файл.

3. Напишите программу, по которой из текстового файла с именем kvur.txt будут прочитаны три числа а, b, с — коэффициенты квадратного уравнения, затем будут вычислены корни этого уравнения и выведены на экран и в текстовый файл korni.txt.

4. Введите из текстового файла целочисленную матрицу размером 6 x 8. Переверните матрицу, поменяв 1-ю строку с 6-й строкой, 2-ю строку с 5-й, 3-ю строку с 4-й и запишите полученную матрицу в другой файл.

5. Введите с клавиатуры одномерный числовой массив из 9 элементов. Сверните его в матрицу размером 3x3, разместив первую тройку элементов в 1-й строке матрицы, 2-ю тройку — во второй строке, 3-ю тройку — в третьей строке. Полученную матрицу выведите на экран и в текстовый файл.

6. Введите с клавиатуры построчно в двумерный массив числовую матрицу размером 4 x 4 Разверните ее по столбцам в одномерный массив. Запишите массив в текстовый файл.

---

Практикум

Работа 3.6. Программирование обработки одномерных массивов

Задание

Составить программу решения поставленной задачи по обработке одномерного массива (вектора). По возможности, использовать подпрограммы.

Уровень 1

1. Дана последовательность действительных чисел а₁, а₂, …, а_n. Выяснить, будет ли она возрастающей.

2. Дан массив из N действительных чисел. Подсчитать, сколько в нем отрицательных, положительных и нулевых элементов.

3. Даны действительные числа а₁, а₂, …, а_n. Поменять местами первый наибольший элемент с последним наименьшим элементом.

4. В заданном одномерном массиве поменять местами соседние элементы, стоящие на четных местах, с элементами, стоящими на нечетных местах.

5. Задана последовательность {X_i} из N вещественных чисел. Вычислить последовательность {S_i} по формуле:

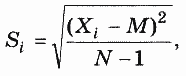
где М — среднее арифметическое значение последовательности X.

6. Задана последовательность из N целых чисел. Вычислить сумму тех элементов массива, порядковые номера которых совпадают со значением этого элемента.

7. Определить, сколько процентов от всего количества элементов последовательности целых чисел составляют нечетные элементы.

8. Дан массив Х_[N] целых чисел. Не используя других массивов, переставить его элементы в обратном порядке. 9. Задана последовательность из N вещественных чисел. Вычислить сумму чисел, порядковые номера которых являются простыми числами.

10. Последовательность а₁, а₂, …, а_2n состоит из нулей и единиц. Поместить в начало этой последовательности все нули, а затем все единицы.

11. Даны действительные числа а₁, а₂, …, а_2n. Найти:

mах(a₁ + а_2n, а₂ +а_2n-1, …, а_n + а_n+1).

12. Дана последовательность действительных чисел a₁ ≤ а₂ ≤ ... ≤ а_n. Вставить действительное число b в нее так, чтобы последовательность осталась неубывающей.

13. Дана последовательность целых чисел а₁, а₂, …, а_n. Указать пары чисел а_i, а_j, таких что a_i + а_j = m, где m - заданное целое число.

14. Даны координаты n (n ≤ 30) точек на плоскости: (Х₁, У₁), ..., (Х_п, Y_n). Найти номера пары точек, расстояние между которыми наибольшее (считать, что такая пара единственная).

15. Дан массив, состоящий из n натуральных чисел. Образовать новый массив, элементами которого будут элементы исходного, оканчивающиеся на цифру k.

16. Дан массив целых чисел. Найти в этом массиве минимальный элемент m и максимальный элемент М. Получить в порядке возрастания все целые числа из интервала (m; М), которые не входят в данный массив.

17. Даны две последовательности а₁, а₂, ..., а_n и b_х, b₂, ..., b_n (m < п). В каждой из них значения элементов различны. Верно ли, что все элементы второй последовательности входят в первую последовательность?

18. Вывести значения и номера наибольшего, наименьшего и наименее удаленного от среднего арифметического значения элементов данной последовательности вещественных чисел.

Уровень 3

19. Сформировать массив простых чисел, не больших заданного натурального числа N.

20. Сформировать массив простых множителей заданного числа.

21. В одномерном массиве все отрицательные элементы переместить в начало массива, а остальные — в конец с сохранением порядка следования. Дополнительный массив заводить не разрешается.

22. В одномерном массиве с четным количеством элементов (2N) находятся координаты N точек плоскости. Они располагаются в следующем порядке: х₁, у₁, х₂, у₂, х₃, у₃, и т. д. Определить:

а) минимальный радиус окружности с центром в начале координат, которая содержит все точки;
б) внутренний и внешний радиусы кольца с центром в начале координат, которое содержит все точки;
в) номера точек, которые могут являться вершинами квадрата;
г) номера точек, которые могут являться вершинами равнобедренного треугольника;
д) номера самых удаленных и наименее удаленных друг от друга точек;
е) три точки, которые являются вершинами треугольника, для которого разность точек вне его и внутри является минимальной.

23. Дана последовательность целых чисел. Найти количество различных чисел в этой последовательности.

24. На плоскости п точек заданы своими координатами, и также дана окружность радиуса R с центром в начале координат. Указать множество всех треугольников с вершинами в заданных точках, пересекающихся с окружностью; множество всех треугольников, содержащихся внутри окружности.

25. Разделить массив на две части, поместив в первую элементы, большие среднего арифметического элементов массива, а во вторую — меньшие (части не сортировать).

26. Даны две последовательности а₁ < а₂ < ... < а_n и b₁ < b₂ < ... < b_m. Образовать из них новую последовательность чисел так, чтобы она тоже была неубывающей.

Примечание. Дополнительный массив не использовать.

27. Сортировка вставками. Дана последовательность чисел а₁, а₂, ..., а_n. Требуется переставить числа в порядке возрастания. Делается это следующим образом. Пусть а₁, а₂, ..., a_i — упорядоченная по неубыванию последовательность, т. е. а₁ < а₂ < ... < а_i. Берется следующее число a_i+1 и вставляется в последовательность так, чтобы новая последовательность была также возрастающей. Процесс производится до тех пор, пока все элементы от i+1 до n не будут перебраны.

Примечание. Место помещения очередного элемента в отсортированную часть найти с помощью двоичного поиска. Двоичный поиск оформить в виде отдельной функции.

28. Алгоритм сортировки фон Неймана. Упорядочить массив а₁, а₂, ..., а_n по неубыванию с помощью алгоритма сортировки слияниями:

1) каждая пара соседних элементов сливается в одну группу из двух элементов (последняя группа может состоять из одного элемента);

2) каждая пара соседних двухэлементных групп сливается в одну четырехэлементную группу и т. д.

При каждом слиянии новая укрупненная группа упорядочивается.

29. Шейкер-сортировка. Алгоритм «пузырьковой» сортировки легко улучшить. Разумно запомнить, производился ли на данном проходе какой-либо обмен. Если нет, то алгоритм можно закончить. Еще одно улучшение заключается в том, что периодически меняется направление сортировки, которое борется с некоторой асимметрией «пузырькового» метода. Написать программу, реализующую данный улучшенный алгоритм.

Работа 3.7. Программирование обработки двумерных массивов

Задание

Составить программу решения поставленной задачи по обработке двумерного массива (матрицы). По возможности, использовать подпрограммы.

Уровень 1

1. Вычислить сумму и число положительных элементов матрицы A[N, N], находящихся над главной диагональю.

2. Дана целая квадратная матрица n-го порядка. Определить, является ли она магическим квадратом, т. е. такой матрицей, в которой суммы элементов во всех строках и столбцах одинаковы.

3. Определить, является ли заданная целая квадратная матрица n-го порядка симметричной (относительно главной диагонали).

4. Дана целочисленная квадратная матрица. Найти в каждой строке наибольший элемент и поменять его местами с элементом главной диагонали в этой же строке.

5. Упорядочить по возрастанию элементы каждой строки матрицы размером n х m.

6. Задана квадратная матрица. Получить транспонированную матрицу (перевернутую относительно главной диагонали).

7. Квадратная матрица, симметричная относительно главной диагонали, задана верхним треугольником в виде одномерного массива. Восстановить исходную матрицу и напечатать по строкам.

8. Задана матрица порядка n и число k. Разделить элементы k-й строки на диагональный элемент, расположенный в этой строке.

9. Для целочисленной квадратной матрицы найти число элементов, кратных k, и наибольший из этих элементов.

10. Найти наибольший и наименьший элементы прямоугольной матрицы и поменять их местами.

11. В данной действительной квадратной матрице порядка п найти сумму элементов строки, в которой расположен элемент с наименьшим значением. Предполагается, что такой элемент единственный.

12. Дана действительная матрица размером n х m. Требуется преобразовать матрицу: поэлементно вычесть последнюю строку из всех строк, кроме последней.

13. Определить наименьший элемент каждой четной строки матрицы А[М, N].

Уровень 2

14. Задана квадратная матрица. Переставить строку с максимальным элементом на главной диагонали со строкой с заданным номером m.

15. Определить номера строк матрицы R[M, N], хотя бы один элемент которых равен с, и элементы этих строк умножить на d.

16. Дана матрица B[N, М]. Найти в каждой строке матрицы максимальный и минимальный элементы и поменять их с первым и последним элементами строки соответственно.

17. Элемент матрицы назовем седловой точкой, если он является наименьшим в своей строке и одновременно наибольшим в своем столбце или, наоборот, является наибольшим в своей строке и наименьшим в своем столбце. Для заданной целой матрицы размером n х m напечатать индексы всех ее седловых точек.

18. Дана вещественная матрица размером n х m. Переставляя ее строки и столбцы, добиться того, чтобы наибольший элемент (или один из них) оказался в верхнем левом углу.

19. Дана квадратная матрица A[N, А]. Записать на место отрицательных элементов матрицы нули, а на место положительных — единицы. Вывести на печать нижнюю треугольную матрицу в общепринятом виде.

20. Дана действительная матрица размером n х m, все элементы которой различны. В каждой строке выбирается элемент с наименьшим значением, затем среди этих чисел выбирается наибольшее. Указать индексы элемента с найденным значением.

21. Дана действительная квадратная матрица порядка N (N — нечетное), все элементы которой различны. Найти наибольший элемент среди стоящих на главной и побочной диагоналях и поменять его местами с элементом, стоящим на пересечении этих диагоналей.

22. Для заданной квадратной матрицы сформировать одномерный массив из ее диагональных элементов. Найти след матрицы, просуммировав элементы одномерного массива. Преобразовать исходную матрицу по правилу: четные строки разделить на полученное значение, нечетные оставить без изменения.

23. Дана прямоугольная матрица. Найти строку с наибольшей и строку с наименьшей суммой элементов. Вывести на печать найденные строки и суммы их элементов.

24. В данной действительной квадратной матрице порядка п найти наибольший по модулю элемент. Получить квадратную матрицу порядка n - 1 путем отбрасывания из исходной матрицы строки и столбца, на пересечении которых расположен элемент с найденным значением.

25. Расположить столбцы матрицы D[M, N] в порядке возрастания элементов k-й строки (1 ≤ k ≤ М).

Уровень 3

26. Среди столбцов заданной целочисленной матрицы, содержащих только такие элементы, которые по модулю не больше 10, найти столбец с минимальным произведением элементов.

27. Для заданной квадратной матрицы найти такие k, что k-я строка матрицы совпадает с k-м столбцом.

28. Найти максимальный среди всех элементов тех строк заданной матрицы, которые упорядочены (либо по возрастанию, либо по убыванию).

29. Составить программу, которая заполняет квадратную матрицу порядка п натуральными числами 1, 2, 3, ..., n², записывая их в нее «по спирали».

Например, для n = 5 получаем следующую матрицу:

30. Среди тех строк целочисленной матрицы, которые содержат только нечетные элементы, найти строку с максимальной суммой модулей элементов.

31. Подсчитать количество строк заданной целочисленной матрицы N х N, являющихся перестановкой чисел 1, 2, ..., N (т. е. содержащих каждое из чисел 1, 2, ..., N ровно один раз).