Урок 11
Моделирование в электронных таблицах

Расчет геометрических параметров объекта

ЗАДАЧА 3.1. Склеивание коробки

I этап. Постановка задачи

ОПИСАНИЕ ЗАДАЧИ

Имеется квадратный лист картона. Из листа по углам вырезают четыре квадрата и склеивают коробку по сторонам вырезов. Какова должна быть сторона вырезаемого квадрата, чтобы коробка имела наибольшую вместимость? Какого размера надо взять лист, чтобы получить из него коробку с заданным максимальным объемом?

ЦЕЛЬ МОДЕЛИРОВАНИЯ

Определить максимальный объем коробки.

ФОРМАЛИЗАЦИЯ ЗАДАЧИ

Проведем формализацию задачи в виде поиска ответов на вопросы.

 

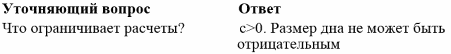
II этап. Разработка модели

ИНФОРМАЦИОННАЯ МОДЕЛЬ

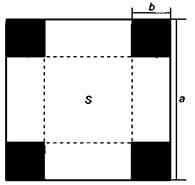
Для вывода формул математической модели составим геометрическую модель в виде чертежа с указанием исследуемых характеристик объекта.

Расчетные параметры объекта определяются по формулам:

с=а—2b — длина стороны дна;

S=c² — площадь дна;

V=Sb — объем.

Здесь а — длина стороны картонного листа, b — размер выреза. Первоначальный размер выреза b₀=0. Последующие размеры выреза определяются по формуле b_i+1=b_i+△b.

КОМПЬЮТЕРНАЯ МОДЕЛЬ

Для моделирования будем использовать среду табличного процессора. В этой среде информационная и математическая модели объединяются в таблицу, которая содержит три области:

♦ исходные данные;
♦ промежуточные расчеты;
♦ результаты.

Заполните область исходных данных по предложенному образцу. В этой области заданы тестовые исходные параметры а=40 см, △b=1 см, которые были использованы для расчета «вручную» длины стороны дна, площади дна и объема коробки при нескольких значениях выреза.

Составьте таблицу расчета по приведенному образцу.

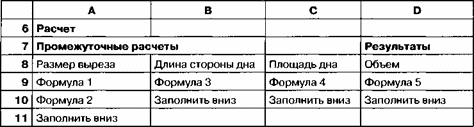
Введите расчетные формулы по правилам, принятым в среде электронных таблиц:

III этап. Компьютерный эксперимент

ПЛАН ЭКСПЕРИМЕНТА

ТЕСТИРОВАНИЕ

Провести тестовый расчет компьютерной модели.

ЭКСПЕРИМЕНТ 1

Проследить, как изменяется с увеличением выреза:
♦ длина стороны дна;
♦ площадь дна;
♦ объем коробки.

ЭКСПЕРИМЕНТ 2

Исследовать, как определить наибольший объем коробки и соответствующий вырез.

ЭКСПЕРИМЕНТ 3

Исследовать, как изменяется наибольший объем коробки и соответствующий вырез при изменении стороны исходного листа.

ЭКСПЕРИМЕНТ 4

Исследовать, как изменяется наибольший объем коробки и соответствующий вырез, если уменьшить шаг изменения выреза (например, при △b=0,3 см).

ЭКСПЕРИМЕНТ 5

Подобрать размер картонного листа, из которого можно сделать картонную коробку с заданным наибольшим объемом (например, 5000 см³).

ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ

ТЕСТИРОВАНИЕ

Сравните результаты, полученные после ввода формул, с результатами, приведенными в примере расчета. Совпадение значений с контрольным образцом показывает правильность введения формул.

Пример расчета для а=40 см, △b=1 см.

ЭКСПЕРИМЕНТ 1. Исследование параметров модели

1. Для проведения исследования заполните в компьютерной модели не менее 20 строк.

2. По столбцу В проследите, как изменяется длина стороны дна. Определите, сколько строк компьютерной модели надо использовать для исследования.

Вывод. Длина стороны дна уменьшается до нуля, а затем становится отрицательной. Для исследования используется диапазон строк, для которых с>0. Общее количество строк с положительными значениями с приблизительно равно а/2.

1. В диапазоне строк, подлежащих исследованию, по столбцу С проследите, как изменяется площадь дна. Сделайте вывод.

2. В диапазоне строк, подлежащих исследованию, по столбцу D проследите, как изменяется объем коробки. Сделайте вывод.

Вывод. Объем коробки сначала увеличивается, достигает некоторого наибольшего значения, затем уменьшается.

ЭКСПЕРИМЕНТ 2. Определение наибольшего объема коробки и соответствующего выреза

1. В диапазоне строк, подлежащих исследованию, по столбцу С определите наибольший объем коробки.

2. По столбцу А определите размер выреза, соответствующий наибольшему объему.

ЭКСПЕРИМЕНТ 3. Зависимость наибольшего объема коробки от размера исходного листа

1. Определите значения наибольшего объема коробки для нескольких значений длины картонного листа. Для этого:
♦ в ячейку В4 введите новое исходное значение;
♦ по столбцу В определите допустимый диапазон строк для исследования. При необходимости заполните дополнительное количество строк; 

2. Результаты экспериментов разместите в ячейках на свободном пространстве электронной таблицы по образцу.
♦ по столбцу D определите наибольший объем коробки;
♦ по столбцу А определите размер выреза, соответствующий наибольшему объему.

3. Сделайте вывод и запишите его после таблицы результатов экспериментов.

ЭКСПЕРИМЕНТ 4. Зависимость наибольшего объема коробки от шага изменения выреза

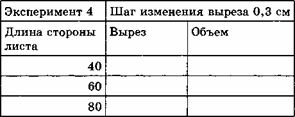
1. Введите в ячейку новое значение шага изменения выреза (например, △b=0,3 см).

2. Определите значения наибольшего объема коробки для нескольких значений длины картонного листа.

3. Результаты экспериментов разместите в ячейках на свободном пространстве электронной таблицы по образцу.

4. Сравните значения наибольшего объема и соответствующего выреза, полученные в 3-м и 4-м экспериментах.

5. Сделайте вывод, позволяет ли уменьшение шага изменения выреза точнее определить наибольший объем и соответствующий вырез. Запишите вывод после таблицы результатов экспериментов. 

ЭКСПЕРИМЕНТ 5. Подбор размера исходного картонного листа

1. Для подбора размера исходного картонного листа изменяйте значение ячейки и определяйте наибольший объем коробки, пока не добьетесь заданной величины.

2. Результаты экспериментов разместите в ячейках на свободном пространстве электронной таблицы по образцу.

IV этап. Анализ результатов моделирования

По результатам экспериментов сформулируйте выводы.

Составьте отчет в текстовом процессоре. В отчете отразите этапы моделирования: исходные данные, геометрическую модель, расчетные формулы, результаты экспериментов и выводы.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

3.2. Определение максимальной площади треугольника.

В прямоугольном треугольнике задана длина гипотенузы с. Найти размеры катетов, при которых треугольник имеет наибольшую площадь. Составить геометрическую и математическую модель. Провести расчеты.

3.3. Определение минимальной длины изгороди садового участка.

Садовый участок прямоугольной формы имеет площадь 5. При каких размерах длины и ширины участка длина изгороди будет наименьшей? Составить геометрическую и математическую модель. Провести расчеты.