Уроки 12 - 14
Моделирование в электронных таблицах
Моделирование ситуаций
ЗАДАЧА 3.4. Обои и комната
I этап. Постановка задачи
ОПИСАНИЕ ЗАДАЧИ
В магазине продаются обои. Наименования, длина и ширина рулона известны. Для удобства обслуживания надо составить таблицу, которая позволит определить необходимое количество рулонов для оклейки любой комнаты.
ЦЕЛЬ МОДЕЛИРОВАНИЯ
Помочь покупателям быстро определять необходимое количество рулонов обоев.
ФОРМАЛИЗАЦИЯ ЗАДАЧИ
Формализуем задачу в виде поиска ответов на вопросы.


II этап. Разработка модели
ИНФОРМАЦИОННАЯ МОДЕЛЬ
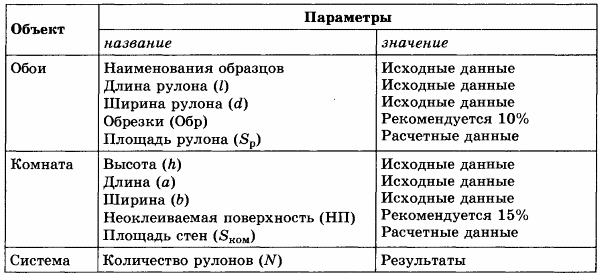
Дополним информационную модель в табличной форме математической моделью.
При расчете фактической площади рулона, которая пойдет на оклейку помещения, надо отбросить обрезки. Формула имеет вид:
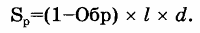
В прямоугольной комнате две стены площадью ah и две стены площадью bh. При расчете фактической площади стен учитывается неоклеиваемая площадь окон и дверей
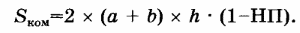
Необходимо также учесть, что количество рулонов должно быть целым числом, но не меньшим, чем значение N.
Количество рулонов, необходимых для оклейки комнаты, вычисляется по формуле
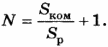
Примечание. Значения, указанные в исходных данных в процентах — Обр и НП, — используются в расчетных формулах в виде числа, получаемого делением процентного значения на 100. При выполнении расчетов в электронных таблицах делить на 100 не надо, так как тип данных Процент воспринимается средой именно как такое число.
КОМПЬЮТЕРНАЯ МОДЕЛЬ
Для моделирования выберем среду табличного процессора. В этой среде информационная и математическая модели объединяются в таблицу, которая содержит три области:
♦ исходные данные;
♦ промежуточные расчеты;
♦ результаты.
Заполните по образцу расчетную таблицу.
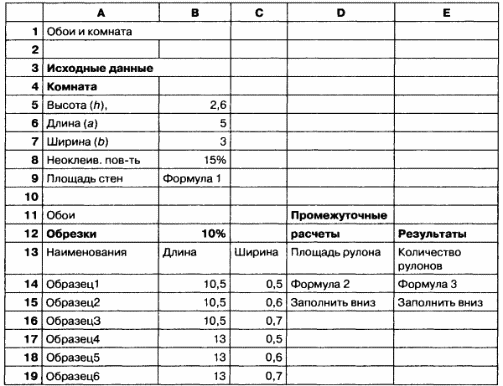
Введите формулы в расчетные ячейки.
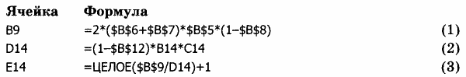
Примечание. Функция ЦЕЛОЕ() округляет до ближайшего целого числа, меньшего, чем заданное. Но поскольку количество рулонов нельзя округлять в меньшую сторону, то к значению функции прибавляем 1 для округления в большую сторону и получаем 1 запасной рулон.
III этап. Компьютерный эксперимент
ПЛАН ЭКСПЕРИМЕНТА
ТЕСТИРОВАНИЕ
Провести тестовый расчет компьютерной модели по данным, приведенным в таблице.
ЭКСПЕРИМЕНТ 1
Провести расчет количества рулонов обоев для помещений вашей квартиры.
ЭКСПЕРИМЕНТ 2
Изменить данные некоторых образцов обоев и проследить за пересчетом результатов.
ЭКСПЕРИМЕНТ 3
Добавить строки с образцами и дополнить модель расчетом по новым образцам.
ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ
1. Введите в таблицу тестовые данные и сравните результаты тестового расчета с результатами, приведенными в таблице.
2. Поочередно введите размеры комнат вашей квартиры и результаты расчетов скопируйте в текстовый редактор.
3. Составьте отчет.
4. Проведите другие виды расчетов согласно плану.
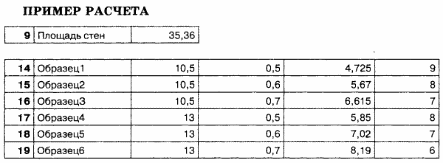
IV этап. Анализ результатов
По данным таблицы можно определить количество рулонов каждого образца обоев для любой комнаты.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
ЗАДАЧА 3.5.
Составить таблицу определения необходимого количества рулонов для типовых размеров комнат.
РЕКОМЕНДАЦИИ ПО РЕШЕНИЮ ЗАДАЧИ
Для построения требуемой таблицы надо воспользоваться моделью задачи 3.4. Результаты экспериментов для различных параметров комнаты копировать и вставлять на свободное пространство электронной таблицы при помощи команды Специальная вставка|Только значения. Оформить таблицу соответствующими пояснениями.
ЗАДАЧА 3.6.
Компьютерный магазин
I этап. Постановка задачи
ОПИСАНИЕ ЗАДАЧИ
Магазин компьютерных аксессуаров продает товары, указанные в прайс-листе. Стоимость указана в долларах. Если стоимость товара превышает некоторую сумму, покупателю предоставляется скидка. Составить таблицу-шаблон, позволяющую быстро рассчитать стоимость произвольной покупки. В расчете учесть текущий курс доллара.
Примечание. Прайс-лист — список товаров с ценами.
ЦЕЛЬ МОДЕЛИРОВАНИЯ
Автоматизировать расчет стоимости покупки.
Составить шаблон расчетной квитанции для покупателя.
ФОРМАЛИЗАЦИЯ ЗАДАЧИ
Проведем формализацию задачи, ответив на вопросы.

II этап. Разработка модели
ИНФОРМАЦИОННАЯ МОДЕЛЬ

Дополним информационную модель в табличной форме математической моделью.

Примечание. Значение, указанное в исходных данных в процентах — Ск, — используется в расчетных формулах в виде числа, получаемого делением процентного значения на 100. При выполнении расчетов в электронных таблицах делить на 100 не надо, так как тип данных Процент воспринимается средой именно как такое число.
КОМПЬЮТЕРНАЯ МОДЕЛЬ
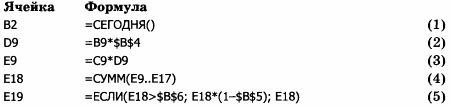
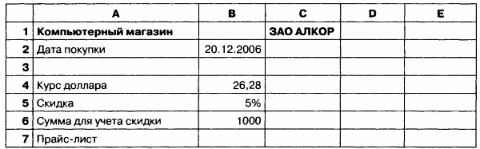
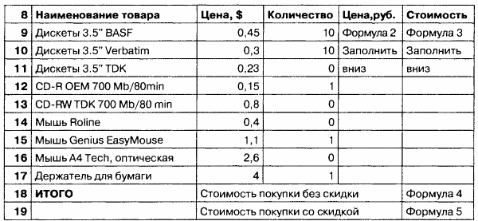
Поскольку одной из целей моделирования является создание шаблона расчетной квитанции для покупателя, то в компьютерной модели надо помимо данных, необходимых для расчета, поместить информацию о названии магазина, дате покупки.
Составьте компьютерную модель по приведенному образцу.
Введите в ячейки исходные данные, расчетные формулы.
III этап. Компьютерный эксперимент
ПЛАН ЭКСПЕРИМЕНТА
ТЕСТИРОВАНИЕ
Провести тестовый расчет компьютерной модели по данным, приведенным в таблице.
ЭКСПЕРИМЕНТ 1
Ввести курс доллара на текущий день, размер скидки и провести расчет покупки со своим количеством товара.
ЭКСПЕРИМЕНТ 2
Добавить строки другими видами товаров и дополнить модель расчетом по этим данным.
ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ
1. Введите в таблицу тестовые данные и сравните результаты тестового расчета с результатами, приведенными в таблице.
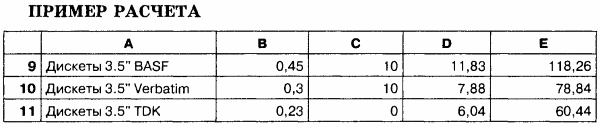
2. Подберите тестовый набор исходных данных, чтобы получить сумму со скидкой.
3. Введите свои исходные данные и проследите за перерасчетом.
4. Проведите другие виды расчетов согласно плану.
IV этап. Анализ результатов моделирования
Полученная модель позволяет автоматически пересчитывать стоимость покупки с любым количеством товара из представленного ассортимента и заполнять расчетную квитанцию.
ЗАДАЧА 3.7. Сберкасса
I этап. Постановка задачи
ОПИСАНИЕ ЗАДАЧИ
За два часа до обеденного перерыва 40 бабушек встали в очередь за пенсией. Кассирша обслуживает клиента в среднем одну минуту.
Первая бабушка «мучила» кассиршу вопросами 9 мин 15 с. Каждая следующая бабушка, частично «мотая на ус» ответы, адресованные предыдущим бабушкам, «мучает» кассиршу на 10 с меньше.
Построить модель ситуации и исследовать ее.
ЦЕЛЬ МОДЕЛИРОВАНИЯ
Цель моделирования учебная: исследовать ситуацию с разных углов зрения (задания типа «что будет, если...», «как сделать, чтобы...»), сделать выводы и дать свои рекомендации по улучшению обслуживания.
ФОРМАЛИЗАЦИЯ ЗАДАЧИ
Чтобы понять суть задачи, ответим на уточняющие вопросы.


II этап. Разработка модели
ИНФОРМАЦИОННАЯ МОДЕЛЬ
Объектом моделирования является система, состоящая из кассира и очереди. Очередь тоже может быть разбита на простые элементы и представляет собой множество из 40 бабушек. Каждый из объектов, входящих в систему, имеет свои параметры. Связи между элементами системы можно схематично изобразить так.
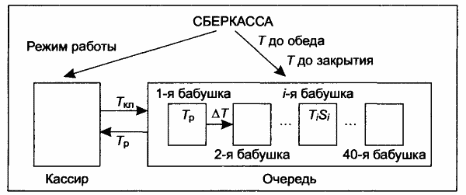
Информационную модель в виде схемы и таблицы дополняет математическая модель ситуации, представленная следующими выражениями.
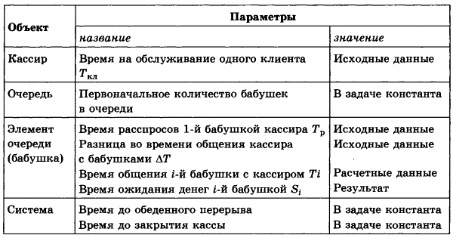

КОМПЬЮТЕРНАЯ МОДЕЛЬ
Объединим информационную и математическую модели, воспользовавшись средой табличного процессора. Для этой задачи промежуточные данные и результаты представляются в виде единого блока, так как в этом блоке содержится вся необходимая информация для анализа и выводов.

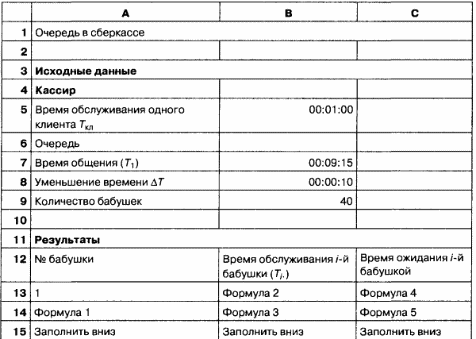
Примечание. В операциях участвуют данные типа Время. Результат выполнения такой операции будет записан в ячейке в числовой форме. Чтобы перевести числовой результат в тип Время, следует использовать опцию Тип данных меню Формат и изменить формат ячейки перед заполнением вниз.
Заполнить таблицу исходными данными. Ввести в таблицу результатов формулы для расчетов.
III этап. Компьютерный эксперимент
ПЛАН ЭКСПЕРИМЕНТА
ТЕСТИРОВАНИЕ
Проверить правильность ввода формул. Произвести расчеты.
ЭКСПЕРИМЕНТ
Изменяя значения ячеек В5, В7, В8, исследовать влияние этих характеристик на скорость движения очереди.
ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ
1. Введите в таблицу контрольные исходные данные и скопируйте расчетные формулы в две-три строки. Результаты сравните с приведенными в таблице.

Сравнение с контрольным образцом показывает правильность введения формул. Это самая простая форма тестирования.
2. Заполните формулами ячейки на 40 строк.
3. Определите по таблице (столбец С), сколько времени понадобится кассиру, чтобы обслужить всю очередь.
4. Найдите в таблице строку, которая соответствует наступлению обеденного перерыва.
IV этап. Анализ результатов моделирования
По результатам моделирования в электронных таблицах ответить на следующие вопросы:
1. Как долго будет «мучить» кассиршу сороковая бабушка?
2. Хватит ли на обслуживание всех бабушек дообеденного времени (2 часа)?
3. Если не хватит, то какую по счету бабушку успеют обслужить до перерыва?
4. Хватит ли времени на обслуживание всей очереди до конца рабочего дня, если после перерыва касса будет открыта еще 4 часа?
5. Как влияет на время обслуживания очереди уменьшение Ткл? Можно ли сильно уменьшить Ткл и к чему это приведет?
6. Как влияет на время обслуживания очереди уменьшение времени расспросов? Можно ли сокращать это время и к чему это приведет?
7. Какие из предыдущих вопросов можно отнести к задаче типа: «что будет, если...», а какие — к задаче «как сделать, чтобы...»?
8. Сформулировать рекомендации символическому кассиру и бабушкам по организации процесса обслуживания. Например, стоит ли выделить отдельного сотрудника, который будет разъяснять возникающие вопросы? Какие другие способы информирования можно использовать? Сколько сотрудников должны работать в кассе, чтобы обслужить клиентов до обеда?
9. Оформить результаты в виде отчета в текстовом процессоре.
ЗАДАЧА 3.8. Нерадивый ученик
I этап. Постановка задачи
ОПИСАНИЕ ЗАДАЧИ
Мальчик учит стихотворение из 40 строк. Чтобы запомнить первую строчку, ему понадобилась всего 1 мин. На каждую следующую он тратит на 10% времени больше. Стихотворение держится в памяти нерадивого ученика не дольше 3 часов, а до школы бежать 15 мин. Как организовать заучивание стихотворения?
ЦЕЛЬ МОДЕЛИРОВАНИЯ
Предлагается исследовать ситуацию и предложить реальные способы ускорения процесса заучивания стихотворения.
ФОРМАЛИЗАЦИЯ ЗАДАЧИ
Ответим на уточняющие вопросы по условию задачи.


II этап. Разработка модели
ИНФОРМАЦИОННАЯ МОДЕЛЬ
Анализ объекта моделирования показывает, что эта система состоит из двух объектов: мальчика и стихотворения. Стихотворение, в свою очередь, может быть разбито на простые элементы — строки. Каждый из объектов, входящих в систему, имеет свои параметры. Связь между объектами этой системы заключается во времени заучивания стиха нерадивым учеником.
Схема связей между элементами системы достаточно проста.
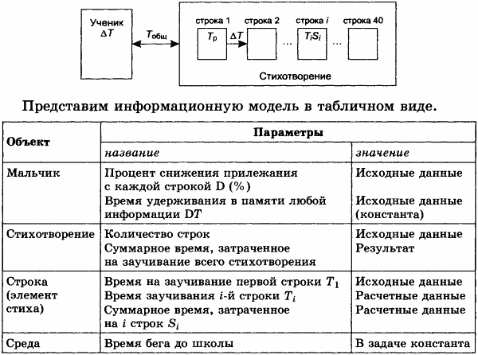
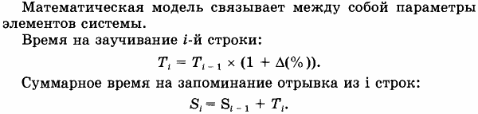
КОМПЬЮТЕРНАЯ МОДЕЛЬ
Объединим информационную и математическую модели, воспользовавшись средой табличного процессора. Для этой задачи промежуточные данные и результаты представляют собой единый блок, в котором содержится вся необходимая информация для анализа и выводов. Заполнить таблицу исходными данными по приведенному образцу.

Примечание. Заполняя в таблице исходные данные, обратите внимание, что значение в ячейку В5 вводится по формату Время, а в ячейку В6 — по формату Процент (число со знаком %). При вводе в ячейку значения в формате Процент в самой ячейке записана процентная форма данного, а в строке состояния высвечивается числовая форма данного.
Ввести формулы для расчетов:

III этап. Компьютерный эксперимент
ПЛАН ЭКСПЕРИМЕНТА
ТЕСТИРОВАНИЕ
Проверить правильность ввода формул.
ЭКСПЕРИМЕНТ 1
Рассчитать в электронных таблицах время заучивания каждой строки стихотворения и суммарное время заучивания. Исследовать полученные результаты.
ЭКСПЕРИМЕНТ 2
Изменяя значения ячеек В5 и В6, исследовать влияние старательности ученика на общее время заучивания стихотворения.
ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ
ТЕСТИРОВАНИЕ
Сравнение с контрольным образцом показывает правильность ввода формул.
Ввести в таблицу контрольные исходные данные и скопировать расчетные формулы в две-три строки. Результаты сравнить с приведенными в таблице.

ЭКСПЕРИМЕНТ 1
Исследование процесса заучивания стихотворения
Скопируйте формулы в нижестоящие ячейки, в общей сложности на 40 строк.
По расчетным данным дайте ответ на следующие вопросы:
1. Сколько времени понадобилось бы мальчику, чтобы выучить все стихотворение?
2. Из скольких строк (максимум) должно состоять стихотворение, если учительница мальчика утверждает, что его знаний хватает не более чем на 3 часа, а до школы бежать 15 мин? Каким по счету может быть урок литературы, чтобы знания «не выветрились» из головы?
3. Сколько строк можно успеть выучить до начала «мультика», если до него осталось 45 мин?
ЭКСПЕРИМЕНТ 2
Исследование влияния старательности на время заучивания стихотворения
Изменяя значения ячеек В5 и В6 в реальных пределах, исследовать их влияние на время заучивания стихотворения.
По расчетным данным дайте ответ на следующие вопросы:
1. Как влияет время заучивания 1-й строки на общее время запоминания стихотворения?
2. Как влияет концентрация внимания (уменьшение D%) на общее время запоминания стихотворения?
IV этап. Анализ результатов моделирования
По результатам, рассчитанным в электронных таблицах, ответить на следующие вопросы:
1. Что нужно изменить в модели заучивания стихов, чтобы просчитать ее для любых других усидчивых и нерадивых учеников? На какой части таблицы это отразится?
2. Что нужно изменить в модели заучивания стихов, чтобы просчитать ее для стихотворения любой длины?
3. Какие из заданных в ходе эксперимента вопросов можно отнести к задаче типа «что будет, если...», а какие — к задаче типа «как сделать, чтобы...»?
4. Предложить реальные способы ускорения процесса заучивания стихотворения.
ЗАДАЧА 3.9*. Расчет кривой падения электрика
(* Задача повышенной сложности)
I этап. Постановка задачи
ОПИСАНИЕ ЗАДАЧИ
Электрик Петров приставил к стене лестницу и, поднявшись вверх, остановился на одной из ступенек. В это время концы лестницы начали скользить вдоль стены и пола. Провести исследование, по какой кривой будет падать вниз электрик Петров.
ЦЕЛИ МОДЕЛИРОВАНИЯ
Исследовать движение лестницы.
ФОРМАЛИЗАЦИЯ ЗАДАЧИ
Проведем формализацию задачи в виде поиска ответов на вопросы.


Будем считать, что лестница первоначально занимала вертикальное положение. Это не совсем реально, но удобно для дальнейших расчетов.
II этап. Разработка модели
ИНФОРМАЦИОННАЯ МОДЕЛЬ
Результаты формализации задачи сведем в таблицу.
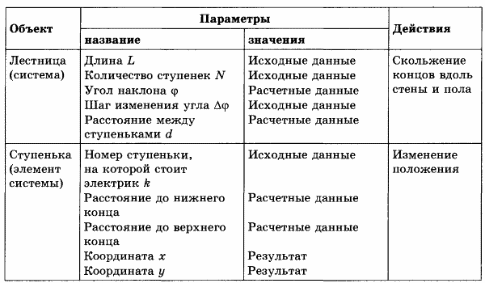
Для построения математической модели воспользуемся чертежом. Так как верхний конец А скользит вдоль стены, то у него изменяется только координата у от L до 0, а координата х всегда равна 0, а для конца В, наоборот, — х изменяется от 0 до L, у = 0. У промежуточных точек изменяются обе координаты.
Вычислим координаты ступеньки с номером k, которая располагается в точке С.

КОМПЬЮТЕРНАЯ МОДЕЛЬ
Для построения компьютерной модели выберем среду табличного процессора. В ней табличная информационная и математическая модели объединяются в таблицу, которая содержит три области:
♦ исходные данные;
♦ промежуточные расчеты;
♦ результаты.
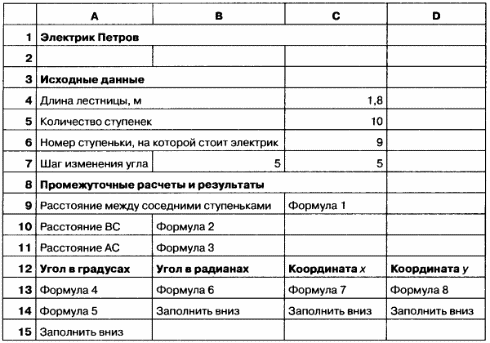
Заполните таблицу по представленному образцу.
Примечание. При использовании встроенных функций SIN() и COS() важно помнить, что угол должен быть выражен в радианах. Введите в расчетные ячейки формулы:

Пример заполнения электронной таблицы.
III этап. Компьютерный эксперимент
ПЛАН ЭКСПЕРИМЕНТА
ТЕСТИРОВАНИЕ
Проверить правильность ввода формул.
ЭКСПЕРИМЕНТ
1. Исследовать вид кривой падения электрика в зависимости от номера ступеньки.
2. Исследовать вид кривой в зависимости от номера ступеньки. ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ
ТЕСТИРОВАНИЕ
1. Сравните результаты, полученные после ввода формул, с результатами, приведенными в примере расчета. Совпадение значений с контрольным образцом показывает правильность введения формул.
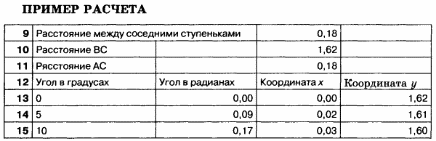
2. По столбцам С и D постройте диаграмму кривой, по которой движется ступенька с электриком.
ЭКСПЕРИМЕНТ. Исследование вида кривой
Постройте диаграммы кривых для различных номеров ступенек и скопируйте их в текстовый документ. Для этого:
♦ Введите в ячейку Сб номер ступеньки. Проследите за пересчетом значений в таблице и изменениями на диаграмме.
♦ Уравняйте масштабы по осям Ох и Оу. Это очень важно, чтобы потом можно было сравнивать виды кривых.
♦ Скопируйте диаграмму в текстовый документ.
♦ Повторите действия для других номеров ступенек.
IV этап. Анализ результатов моделирования
1. Просмотрите диаграммы кривых различных номеров ступенек.
2. Убедитесь, что кривая похожа на четверть эллипса, сплющенного или к оси ординат (если номер ступеньки больше 5), или к оси абсцисс (если номер ступеньки меньше 5). А на что похожа кривая, если номер ступеньки, на которой стоит электрик, равен 5?
3. Сформулируйте и запишите выводы по результатам исследования в текстовый документ.
ЗАДАЧА 3.10*. Дачник и собака
* Задача повышенной сложности.
I этап. ПОСТАНОВКА ЗАДАЧИ
ОПИСАНИЕ ЗАДАЧИ
От железнодорожной станции по направлению к дачному поселку движется пешеход. Одновременно с ним в том же направлении бежит собака. Поскольку собака бежит быстрее, то, добежав до дома и радостно известив о приближении хозяина, она разворачивается и бежит к человеку, а от него обратно к дому...
Какой суммарный путь пробежит собака за время, пока человек дойдет до дома?
ЦЕЛЬ МОДЕЛИРОВАНИЯ
Исследовать процесс движения объектов: человека и собаки. Установить связь между расстояниями, пройденными объектами за одно и то же время. Определить путь, который пробежала собака.
ФОРМАЛИЗАЦИЯ ЗАДАЧИ
Проведем формализацию задачи в виде поиска ответов на следующие вопросы.


II этап. Разработка модели
ИНФОРМАЦИОННАЯ МОДЕЛЬ
На рисунке 3.1 представлены объекты и параметры системы. Рисунок позволяет наглядно представить процесс движения.
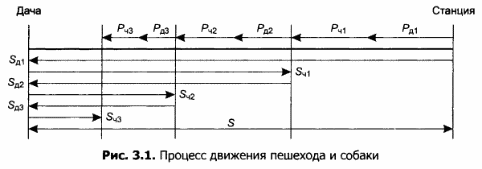
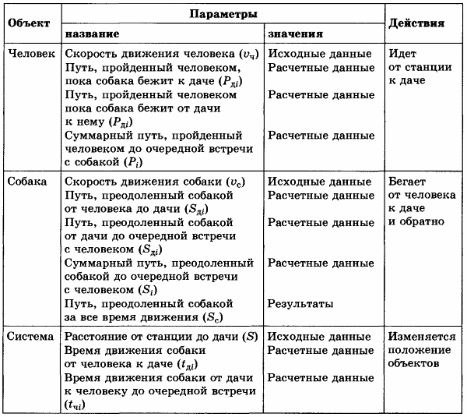
Составим математическую модель, связывающую параметры движения системы.
Рассмотрим два отрезка движения:
♦ собака бежит от человека к даче;
♦ собака бежит от дачи к человеку (первая встреча).
Параметры движения собаки от человека к даче определяются по формулам:
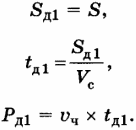
Параметры движения собаки от дачи к человеку до их первой встречи определяются по формуле:
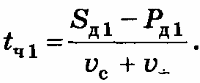
Эта формула получается следующим образом. Расстояние, которое было между человеком и собакой, когда они начинают двигаться навстречу друг другу, равно Sд1 - Рд1. Оно также может быть представлено как сумма расстояний, пройденных каждым участником до встречи Vc х tч1 + Vч1 х tч1. Поскольку собака и человек движутся навстречу друг другу, то время движения до встречи у них одинаковое. Но так как скорости разные, то расстояния, которые они пройдут, тоже разные. Приравняем эти выражения:
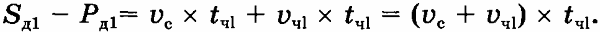
Будем строить модель пути, пройденного собакой, как сумму отрезков, которые она пробегает от человека до дачи и обратно. Обозначим их S1, S2, S3,... Путь, пройденный собакой от момента расставания с человеком у станции до новой встречи с ним: S1 = Sд1 + Sч1.
КОМПЬЮТЕРНАЯ МОДЕЛЬ
Для построения компьютерной модели выбираем среду табличного процессора, которая содержит три области:
♦ исходные данные;
♦ промежуточные расчеты;
♦ результаты.
1. Заполните область исходных данных по образцу.
2. Для суммирования в результирующем столбце G отрезков пути, пройденных собакой, в ячейку G9 введите 0 (ноль) — путь, пройденный собакой в начальный момент времени.
3. Заполните расчетные ячейки по формулам:

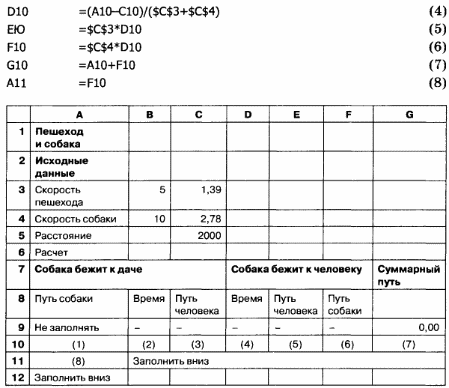
III этап. Компьютерный эксперимент
ПЛАН ЭКСПЕРИМЕНТА
ТЕСТИРОВАНИЕ
Провести тестовый расчет компьютерной модели.
ЭКСПЕРИМЕНТ
Провести расчеты с различными исходными значениями скоростей объектов и расстояния между станцией и дачей.
ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ
1. Введите в таблицу тестовые данные и сравните результаты тестового расчета с результатами, приведенными ниже.
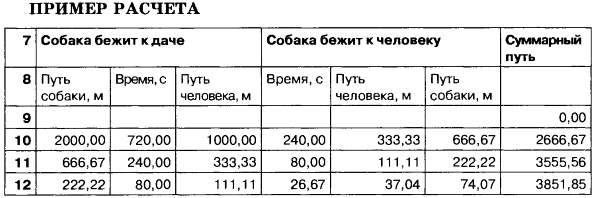
2. Измените скорость человека и проследите, как это отразится на результатах.
3. Измените расстояние между пунктами.
4. Измените скорость собаки.
IV этап. Анализ результатов моделирования
Ответить на вопрос, поставленный в задаче. Оформить выводы и результаты расчетов в текстовом редакторе.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
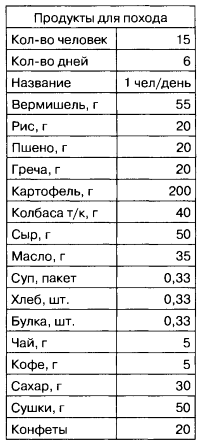
3.11. Продукты для похода.
Для организации похода надо построить модель расчета нормы продуктов для группы туристов. Известна норма каждого продукта на 1 человека на 1 день, количество человек и количество дней похода.
Рассчитать необходимое количество продуктов на весь поход для 1 человека и для всей группы. Провести расчеты для разных исходных значений количества дней и туристов. Нормы продуктов приведены в таблице.
3.12. Концентрация раствора.
В магазине продается 70%-ный раствор уксусной эссенции. Для домашних нужд обычно используется раствор меньшей концентрации и в разных количествах. Примеры приведены в таблице. Составьте таблицу, по которой можно определить, как изменяется исходная концентрация при добавлении 1, 2, 3 и т. д. частей воды. По таблице определите, сколько надо взять частей воды на 1 часть уксусной эссенции, чтобы получить нужное количество раствора требуемой концентрации, а также подберите вес исходной части раствора (и воды), чтобы получить требуемое количество разбавленного раствора. Исходными данными являются:
• исходная концентрация раствора;
• вес 1 части раствора исходной концентрации (и 1 части воды).

3.13. Буратино и папа Карло.
У папы Карло было накоплено 20 золотых, когда Буратино поступил на работу в кукольный театр Карабаса Барабаса. Еженедельно Буратино приносит зарплату 5 золотых, а папа Карло тратит половину (50%) имеющегося на начало недели богатства. Постройте модель изменения капитала в течение нескольких недель. Исследуйте модель и ответьте на вопросы:
1. Как изменяется капитал, если увеличить (уменьшить) начальный капитал папы Карло?
2. Как изменяется капитал, если увеличить (уменьшить) зарплату Буратино?
3. Как изменяется капитал, если увеличить (уменьшить) процент еженедельной траты капитала?
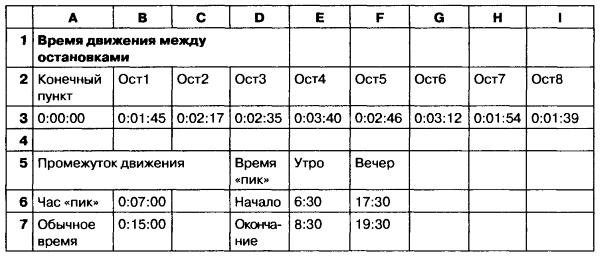
3.14. Расписание движения автобуса.
Маршрут автобуса включает 8 остановок. Время движения между остановками задано массивом. Составить расписание движения автобуса в течение рабочего дня, учитывая следующие условия:
• время работы маршрута 5:30-24:00;
• частота движения автобуса на маршруте зависит от времени дня и составляет в часы «пик» с 6:30 до 8:30 и с 17:30 до 19:00 — 7 мин; в остальное время дня — 15 мин.
3.15. График тренировки.
Начав тренировки, спортсмен в первый день пробежал 10 км. Каждый следующий день он пробегал на 10% больше предыдущего. Построить таблицу «График тренировок», в которой имеются следующие столбцы:

По таблице определить:
1. Суммарный пробег за 7 дней.
2. Через сколько дней спортсмен будет пробегать в день более 20 км.
3. Через сколько дней суммарный пробег превысит 100 км.
3.16. Аквариум.
Мальчик решил почистить аквариум. Начал с переселения рыбок в банку. Семейство рыбок, проживающих в аквариуме, составляло 40 штук. Первую рыбку он поймал быстро, затратив 5 с, и еще 2 с потратил на перекладывание в банку. Но чем меньше становилось в воде рыбок, тем труднее было их поймать. На каждую следующую рыбку он затрачивал времени больше на 5%, чем на предыдущую.
Сколько минут он затратит на переселение рыбок?
3.17. Награда.
Шахматы были изобретены в Индии. Индусский царь Шерам решил наградить изобретателя шахмат, вызвал его к себе и сказал, что исполнит любую его просьбу. Изобретатель удивил царя беспримерной скромностью просьбы:
— Прикажи выдать мне за первую клетку шахматной доски 1 пшеничное зерно, за вторую — 2, за каждую следующую в два раза больше, чем за предыдущую.
Сколько килограммов зерен было выдано изобретателю, если 1 зерно весит 0,05 г?

