Уроки 17 - 18
Моделирование в электронных таблицах
Моделирование движения тела под действием силы тяжести
Примеры движения под действием силы тяжести хорошо известны. Это и падение тела с некоторой высоты, и движение тела, брошенного вверх с некоторой скоростью, и движение тела, брошенного под углом к горизонту. Если в таких задачах не учитывать силу сопротивления воздуха, то все перечисленные виды движения описываются известными формулами. Но задачи, в которых сопротивление воздуха учитывается, не менее интересны.
ЗАДАЧА 3.24. Поражение цели
I этап. Постановка задачи
ОПИСАНИЕ ЗАДАЧИ
Мальчики играют в бадминтон. Порыв ветра подхватил волан и отнес его на ветви дерева. Предстоит нелегкая задача — достать волан. Задачу можно решить несколькими способами. Каждый из способов имеет свои плюсы и минусы.
Можно, например, залезть на дерево. Но это очень опасное занятие: ветки дерева чем выше, тем тоньше. Велика вероятность падения. Можно спилить дерево. Но, видимо, еще никто не опробовал такой путь решения задачи. Если бы все выбирали такой способ решения задачи, то давно бы уже не осталось ни одного дерева. Можно ждать, когда волан упадет сам, подхваченный очередным порывом ветра. Наиболее часто волан пытаются сбить камнем. Выберем эту модель поведения и мы. Тем более, что нам известны законы движения тела.
ЦЕЛЬ МОДЕЛИРОВАНИЯ
Исследовать движение тела, брошенного под углом к горизонту. Подобрать начальные значения скорости и угла бросания так, чтобы брошенное тело попало в цель.
ФОРМАЛИЗАЦИЯ ЗАДАЧИ

Примечание. Чтобы задать точность попадания △, надо учитывать размеры тела.
Точность попадания △ должна быть не более половины наименьшего геометрического размера тела.
Так, например, если цель — волан размером в диаметре примерно 7 см, то △ = 3,5 см. Если цель — баскетбольное кольцо диаметром 40 см, то △ = 20 см. Если цель — аэростат высотой 5 м, то △ = 2,5 м.
II этап. Разработка модели
ИНФОРМАЦИОННАЯ МОДЕЛЬ
Характеристики объектов и процесса представим в виде таблицы.
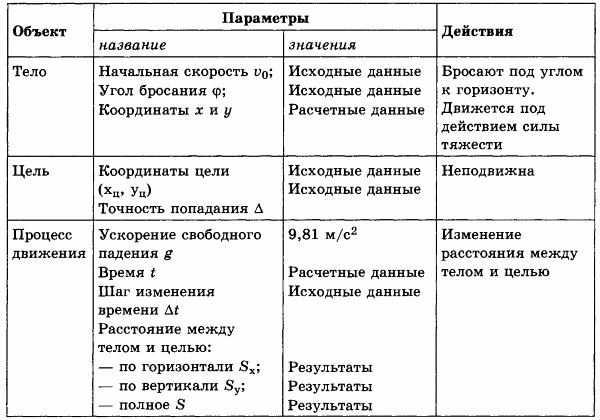
Параметры движения тела представлены на рисунке 3.4. Движение тела, брошенного под углом к горизонту, описывается формулами
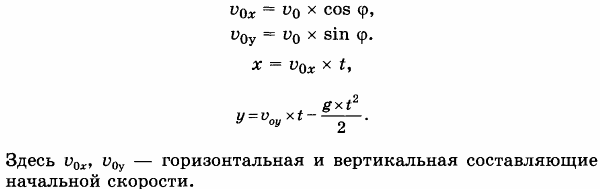
КОМПЬЮТЕРНАЯ МОДЕЛЬ
Для моделирования выберем среду табличного процессора. В этой среде табличная информационная и математическая модели объединяются в таблицу, которая содержит три области:
♦ исходные данные;
♦ промежуточные расчеты;
♦ результаты.
1. Заполните область исходных данных по образцу.
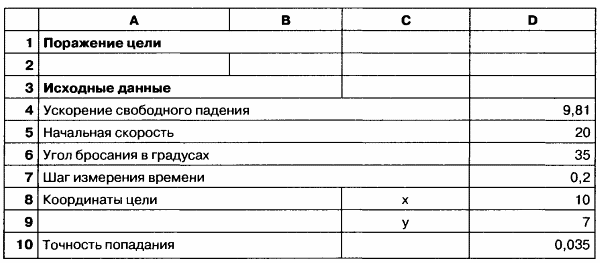
Столбцы А, В, С, D, Е, F заполнить сверху вниз аналогичными формулами.
2. Заполните область промежуточных рассчетов и результатов.

III этап. Компьютерный эксперимент
ПЛАН ЭКСПЕРИМЕНТА
ТЕСТИРОВАНИЕ
Провести тестовый расчет компьютерной модели по данным, приведенным в таблице.
ЭКСПЕРИМЕНТ 1
Исследовать движение тела.
ЭКСПЕРИМЕНТ 2
Исследовать изменение движения тела при изменении начальной скорости.
ЭКСПЕРИМЕНТ 3
Исследовать изменение движения тела при изменении угла бросания.
ЭКСПЕРИМЕНТ 4
Изменяя начальную скорость и угол бросания, исследовать характер движения тела и его положение по отношению к цели.
ЭКСПЕРИМЕНТ 5
Изменяя исходную начальную скорость и угол, подобрать значения так, чтобы брошенное тело попало в цель с заданной точностью.
ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ
ТЕСТИРОВАНИЕ
1. Заполните столько строк расчетной таблицы, пока координата у не станет меньше нуля.
2. Сравните результаты тестового расчета с результатами, приведенными в примере расчета. Ниже в таблице представлено несколько строк с результатами расчетов по приведенным исходным данным.
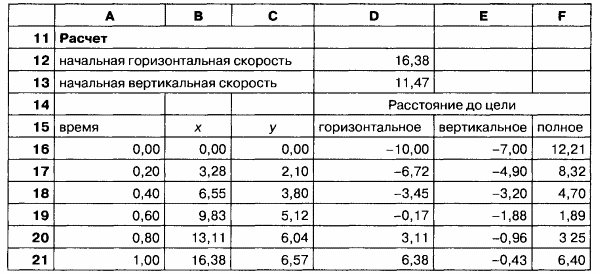
3. По столбцам В и С построить диаграмму движения. Пример представлен на рисунке 3.6. Для построения диаграммы возьмите столько расчетных значений, чтобы кривая пересекла горизонтальную ось х.
4. Как определить, сколько расчетных точек надо взять для построения диаграммы?
Вывод. Для построения диаграммы надо взять расчетные значения, у которых координата
y больше 0, и одно отрицательное значение.
ЭКСПЕРИМЕНТ 1. Исследование движения тела
1. По диаграмме тестового примера опишите, как движется тело.
2. Объясните, как по диаграмме определить точку наивысшего подъема тела.
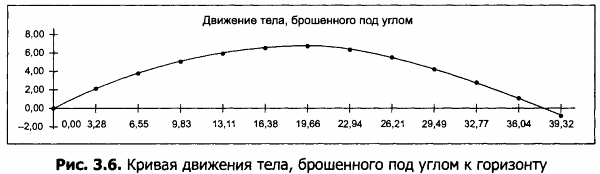
3. Объясните, что на диаграмме обозначает точка пересечения кривой с горизонтальной осью х. Как по таблице расчетов определить эту точку?
4. Определите по диаграмме, на каком расстоянии от точки броска тело упадет на землю.
5. Определите по таблице расчетов:
• наибольшую высоту подъема;
• время движения до наивысшей точки;
• расстояние от точки броска до точки падения на землю;
• время движения до падения.
В свободной области электронной таблицы запишите результаты исследования движения тела по предложенному образцу.

6. Введите другой вариант исходных данных, заполните для них таблицу результатов эксперимента.
ЭКСПЕРИМЕНТ 2. Зависимость движения тела от начальной скорости (угол бросания неизменный)
1. Изменяя начальную скорость от 5 до 20 м/с, проследите, как изменяется наибольшая высота подъема (координата у) при увеличении начальной скорости.
2. Проследите, как изменяется дальность полета (координата x) при увеличении начальной скорости.
3. Проведите расчеты для некоторого угла и результаты исследований сведите в таблицу (таблица 2), составленную на свободном поле электронной таблицы.
4. Запишите в таблицу выводы по результатам эксперимента: как изменяется высота и дальность полета при изменении начальной скорости (при неизменном угле бросания)?

ЭКСПЕРИМЕНТ 3. Зависимость движения тела от угла бросания (начальная скорость движения неизменна)
1. Проведите расчеты по модели, увеличивая угол бросания от 5° до 85° и оставляя неизменной начальную скорость (например, 15 м/с).
2. Проследите изменение высоты подъема (координата у) при увеличении угла бросания, начальная скорость неизменна.
3. Проследите изменение дальности полета (координата x) при увеличении угла бросания.
4. Результаты расчетов сведите в таблицу на свободном поле электронной таблицы (таблица 3).

5. Запишите в таблицу выводы по результатам эксперимента: как изменяется высота и дальность полета при изменении угла бросания (при неизменной начальной скорости)?
ЭКСПЕРИМЕНТ 4. Исследование характера движения тела и его положения по отношению к цели
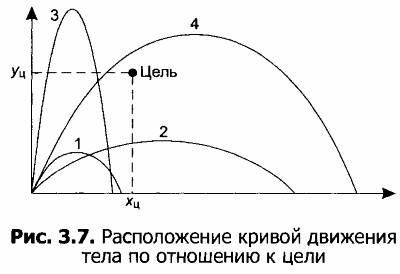
На рисунке 3.7 показаны варианты расположения кривой движения тела по отношению к цели. Их можно охарактеризовать следующим образом:
1. Тело при движении не достигает высоты, на которой расположена цель, и падает на землю, не достигая Xц.
2. Тело при движении не достигает высоты, на которой расположена цель, но падает на землю дальше Xц.
3. Тело при движении поднимается выше Yц, но падает на землю, не достигая Xц.
4. Тело при движении поднимается выше Yц и падает на землю дальше Xц.
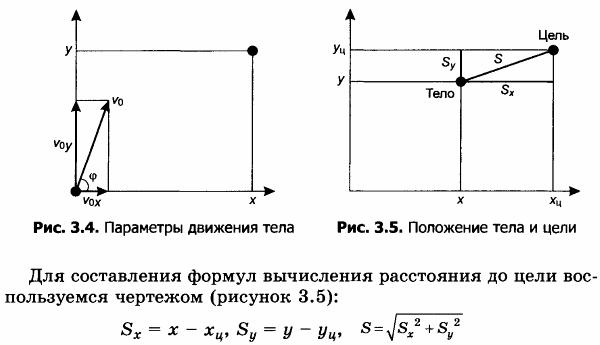
В столбцах D, Е и F вычисляются величины Sx, Sy, S, которые показывают расположение тела по отношению к цели.
1. Исследуйте, что означает знак Sx и Sy в различные моменты времени.
Вывод.

2. Исследуйте, как изменяется S при движении тела.
Вывод. Полное расстояние до цели сначала уменьшается, а потом увеличивается.
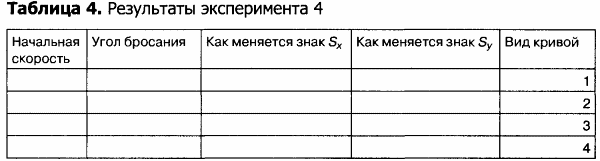
3. Подберите исходные данные (начальную скорость и угол бросания), соответствующие вариантам движения тела, представленным на рисунке 3.7, на свободном поле электронной таблицы (таблица 4).
ЭКСПЕРИМЕНТ 5. Подбор исходных значений для попадания в цель
Прежде всего заметим, что существует бесконечное множество вариантов исходных данных для попадания в цель. Наша задача — подобрать один вариант.
1. По столбцу F определите наименьшее значение S. В этот момент тело ближе всего пролетает к цели.
2. Постройте столбец G анализа попадания. Будем считать, что тело попало в цель, если расстояние до цели стало меньше заданной точности (ячейка $D$10). Для этого в ячейку G16 введите формулу =ЕСЛИ(F16<$D$10; «попал»; «мимо»).
3. Изменяйте исходные данные, чтобы получить наилучшее приближение к цели.
4. Результаты исследования запишите на свободном поле электронной таблицы (таблица 5).
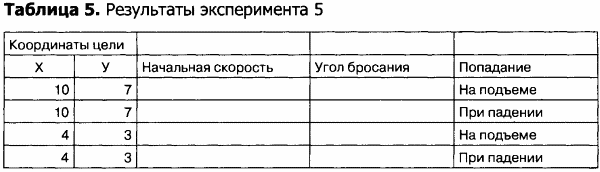
5. Подберите еще один набор исходных данных, при котором тело попадет в цель «навесом», то есть после прохода наивысшей точки подъема.
6. Измените координаты цели и подберите значения начальной скорости и угла бросания для нового положения цели.
IV этап. Анализ результатов моделирования
Результаты и выводы, полученные в экспериментах, оформите в виде отчета в текстовом документе. В отчете приведите ответы на следующие вопросы:
1. Как движется тело, брошенное под углом к горизонту?
2. Как определить наивысшую точку подъема?
3. Как определить дальность полета?
4. Как изменяется наибольшая высота подъема при увеличении начальной скорости и неизменном угле броска?
5. Как изменяется дальность полета при увеличении начальной скорости и неизменном угле броска?
6. Как изменяется наибольшая высота подъема при увеличении угла бросания и неизменной начальной скорости?
7. Как изменяется дальность полета при увеличении угла бросания и неизменной начальной скорости?
8. Как по расчетам определить положение тела по отношению к цели в каждый момент времени? Как это определить по таблице расчетов?
9. Как изменяется расстояние от тела до цели при движении и как это определить по таблице расчетов?
ЗАДАЧА 3.25*. Движение парашютиста
* Задача повышеной сложности
I этап. Постановка задачи
ОПИСАНИЕ ЗАДАЧИ
Парашютист при падении к земле испытывает действие силы тяжести и силы сопротивления воздуха. Экспериментально установлено, что сила сопротивления зависит от скорости движения: чем больше скорость, тем больше сила. При движении в воздухе эта сила пропорциональна квадрату скорости с некоторым коэффициентом сопротивления k, который зависит от конструкции парашюта и веса человека Rсопр = kV2.Каково должно быть значение этого коэффициента, чтобы парашютист приземлился на землю со скоростью не более 8 м/с, не представляющей опасности для здоровья?
Определите цели моделирования и проведите формализацию задачи.
II этап. Разработка модели
ИНФОРМАЦИОННАЯ МОДЕЛЬ
Составьте информационную модель самостоятельно.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
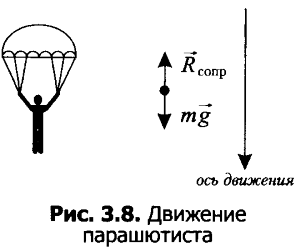
На рисунке 3.8 указаны силы, действующие на парашютиста. Согласно второму закону Ньютона движение под действием сил можно записать равенством. Проецируем это равенство на ось движения, подставим выражение для силы сопротивления воздуха mа = mg — kV2.
Получим формулу для вычисления ускорения
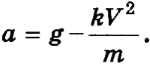
Будем рассчитывать скорость и расстояние, которое пролетел парашютист через равные промежутки времени △t. Формула для вычисления моментов времени имеет вид: ti+1 + ti + △t.
Будем также считать, что на каждом промежутке ускорение постоянно и равно аi. Формула для вычисления ускорения имеет вид
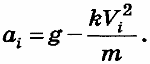
где Vi — скорость в начале промежутка (Vo — начальная скорость). Скорость в конце промежутка (и, соответственно, в начале следующего) вычисляется по формуле равноускоренного движения
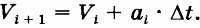
Расстояние, которое пролетел парашютист, равно сумме расстояния, пройденного к началу очередного промежутка времени (Si), и расстояния, пройденного на этом промежутке:
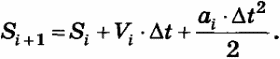
КОМПЬЮТЕРНАЯ МОДЕЛЬ
Для моделирования выберем среду электронной таблицы. В этой среде информационная и математическая модели объединяются в таблицу, которая содержит три области:
♦ исходные данные;
♦ промежуточные расчеты;
♦ результаты.
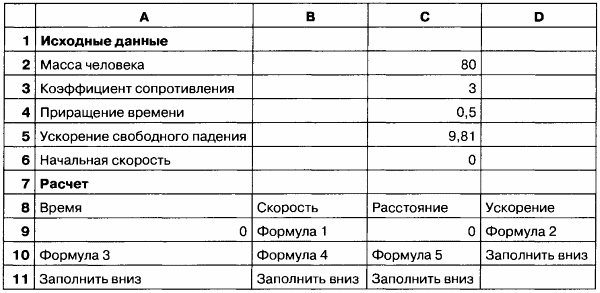
1. Заполните область исходных данных.
2. Заполните расчетные столбцы А, В, С, D, в которых вычисляются параметры движения парашютиста:
• время;
• скорость;
• расстояние;
• ускорение.
3. Введите формулы в расчетные ячейки. Пример заполнения расчетной таблицы:

III этап. Компьютерный эксперимент
ПЛАН ЭКСПЕРИМЕНТА
ТЕСТИРОВАНИЕ
Провести тестовый расчет компьютерной модели по данным, приведенным в таблице.
ЭКСПЕРИМЕНТ 1
Исследовать движение тела под действием силы тяжести и сопротивления воздуха.
ЭКСПЕРИМЕНТ 2
Подобрать значение коэффициента сопротивления k для безопасного приземления парашютиста.
ЭКСПЕРИМЕНТ 3
Исследовать зависимость скорости, ускорения от начальной скорости движения.
ЭКСПЕРИМЕНТ 4
Исследовать, как изменяется расстояние полета до стабилизации скорости падения.
ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ
ТЕСТИРОВАНИЕ
1. Сравните результаты тестового расчета с результатами, приведенными в примере расчета. Пример тестового расчета:

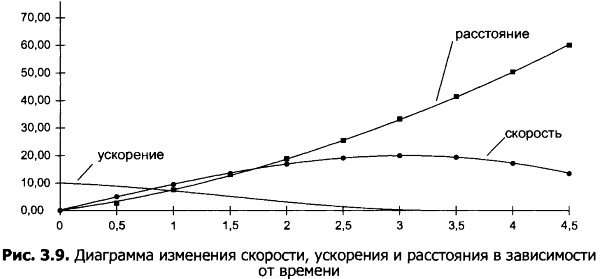
2. Постройте диаграмму изменения скорости, ускорения и расстояния в зависимости от времени.
ЭКСПЕРИМЕНТ 1. Исследование движения тела с учетом сопротивления воздуха
1. Определите по диаграмме и по таблице, как изменяется с течением времени скорость движения парашютиста. Через сколько секунд наступает стабилизация скорости падения?
2. Определите по диаграмме и по таблице, как изменяется с течением времени ускорение парашютиста.
3. Определите по диаграмме и по таблице, какое расстояние пролетит парашютист до стабилизации скорости движения. Результаты поместите на свободном поле в электронной таблице.
4. Измените шаг времени (0,1 с) и определите скорость стабилизации движения, расстояние полета до стабилизации. Результаты исследования приведите в таблице.
ЭКСПЕРИМЕНТ 2. Подбор коэффициента сопротивления
Изменяя значение коэффициента k (ячейка СЗ), подберите скорость стабилизации движения, безопасную для приземления тренированного человека (8 м/с).
ЭКСПЕРИМЕНТ 3. Исследование стабилизации скорости и расстояния в зависимости от начальной скорости
Парашютист, выпрыгнув из самолета, некоторое время летит в свободном падении, набирает достаточно большую скорость движения и только потом раскрывает парашют.
1. Измените значение начальной скорости (10 м/с).
2. По таблице расчетов определите, как изменится:
• начальное ускорение;
• скорость стабилизации;
• расстояние полета до стабилизации скорости.
3. Результаты эксперимента запишите на свободном поле электронной таблицы. Сделайте вывод.
Результаты эксперимента 3:

Примечание. Обратите внимание, как изменяется начальное ускорение. Учтите, что оно не может быть большим, так как ускорение более 3g (30 м/с2) вызывает очень большие перегрузки.
IV этап. Анализ результатов моделирования
По результатам компьютерного эксперимента ответить на следующие вопросы:
1. Как изменяется скорость парашютиста с течением времени?
2. Как изменяется скорость парашютиста при изменении коэффициента сопротивления?
3. Каким должен быть коэффициент сопротивления, чтобы парашютист опустился на землю со скоростью 8 м/с?
4. Как изменяется скорость движения и как зависит установившаяся скорость равномерного движения парашютиста от начальной скорости?
5. Через сколько секунд после начала движения скорость парашютиста можно считать установившейся?
6. На какой высоте от земли парашютист должен раскрыть парашют, чтобы приземлиться с заданной скоростью.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
3.26. Баскетболист.
Пользуясь построенной моделью движения тела, брошенного под углом, рассчитать, с какой начальной скоростью и под каким углом нужно бросить баскетбольный мяч, чтобы попасть в кольцо.
При расчетах учесть следующие условия:
• начальная скорость мяча при броске может изменяться в пределах до 15 м/с;
• координаты кольца у = 3 м, х = 0,5 ÷ 7 м;
• точность попадания связана с диаметром кольца и равна △ = 20 см;
• мяч должен попасть в кольцо «навесом», то есть после прохода наивысшей точки подъема.
РЕКОМЕНДАЦИИ К РЕШЕНИЮ ЗАДАЧИ
Измените математическую и компьютерную модели движения тела, брошенного под углом, так, чтобы по ним можно было рассчитать движение тела, брошенного с некоторой начальной высоты
y0
3.27. Спасение утопающего.
С какой скоростью и под каким углом надо бросить с борта спасательного судна круг утопающему? При расчетах учесть следующие условия:
• начальная скорость может изменяться в пределах до 10 м/с;
• расстояние утопающего от корабля;
• точность попадания равна △ = 0,5 м;
• угол бросания может быть отрицательным;
• высоту борта корабля над уровнем моря.
3.28. Акробаты.
Многие видели в цирке такой акробатический номер. Один акробат встает на прыжковую доску с одной стороны, второй прыгает на другой конец. С какой начальной скоростью и под каким углом должен взлететь вверх первый акробат, чтобы опуститься точно на плечи третьего участника номера? При расчетах учесть следующие условия:
• начальная скорость может изменяться в пределах до 10 м/с;
• высоту и удаление третьего акробата;
• точность попадания равна △ = 0,1 м.

