Урок 19
Моделирование в электронных таблицах

Моделирование экологических систем

Вычислительная техника открыла широкие возможности для изучения процессов, происходящих в природе и обществе. Среди задач, успешно моделируемых на компьютерах, особое место занимают экологические. Круг их очень велик. С одной стороны — это задачи развития биологических видов в природной среде, с другой — исследование влияния деятельности человека на природу. Моделирование в экологической сфере позволяет прогнозировать развитие биологических популяций, управлять численностью отдельных видов и предсказывать влияние угрожающих их развитию факторов.

ЗАДАЧА 3.29. Изменение численности биологического вида

I этап. Постановка задачи

ФОРМУЛИРОВКА ЗАДАЧИ

В некоторой природной среде обитает один или несколько видов живых организмов. Они могут иметь разную среду обитания, разные источники питания, то есть различные внешние факторы, влияющие на численность.

Жизнь некоторых популяций идет обособленно, они занимают свою «экологическую нишу». Их численность практически не зависит от наличия соседствующих видов. Некоторые виды, хотя и не угрожают напрямую жизни соседствующих видов, но имеют с ними общую среду обитания и (или) одни и те же источники питания. Про такие виды говорят, что они соперничают друг с другом. Виды могут враждовать, когда один вид охотится за другим и уничтожает его.

Требуется исследовать изменение численности популяций в разных условиях.

ЦЕЛЬ МОДЕЛИРОВАНИЯ

► Исследование изменения численности популяции при разных коэффициентах рождаемости и смертности, с учетом природных факторов и биологического взаимодействия видов. Чем больше внешних факторов учитывается при расчете, тем более точной и реалистичной получается модель.

► Построение моделей с различной степенью огрубления природного процесса и принятие решения о целесообразности дальнейшего уточнения модели.

► Корректировка модели и исследование влияния дополнительных входных параметров на выходные характеристики.

► Прогнозирование неблагоприятных факторов (например, нехватки ресурсов), приводящих к вымиранию популяции.

ФОРМАЛИЗАЦИЯ ЗАДАЧИ

В этой задаче моделируется процесс изменения численности популяции, развивающейся обособленно или в составе биологической системы. Численность вида зависит от разных факторов: рождаемости, смертности, выживаемости в данных природных условиях и т. д.

МОДЕЛЬ 1. Зависимость роста численности популяции от рождаемости

I этап. Уточненная постановка задачи

Одноклеточная амеба каждые 3 часа делится на две клетки. Построить модель изменения количества клеток через 3, 6, 9, 12, ... часов. Факторы, приводящие к гибели амеб, не учитываются.

II этап. Разработка модели

ИНФОРМАЦИОННАЯ МОДЕЛЬ

Математическая модель изменения численности амеб:

Ч_i+1 = Ч_i х КР,

где Ч_i — количество клеток через i промежутков времени; Ч_i+1 — количество клеток через i+1 промежуток времени (то есть спустя 3 часа); КР — коэффициент рождаемости.

КОМПЬЮТЕРНАЯ МОДЕЛЬ

Для моделирования выберем среду табличного процессора. В этой среде информационная модель представляется в виде таблицы, которая содержит две области:

► исходные данные;
► расчетные данные (результаты).

Ввести в верхнюю часть таблицы исходные данные, а в расчетную часть таблицы — следующие формулы:

III этап. Компьютерный эксперимент

ПЛАН ЭКСПЕРИМЕНТА

ТЕСТИРОВАНИЕ

Проверить правильность ввода формул.

ЭКСПЕРИМЕНТ

1. Произвести расчеты роста численности популяции.

2. По результатам расчетов построить диаграмму.

ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ

1. Введите в таблицу контрольные исходные данные и скопируйте расчетные формулы в две-три строки. Результаты сравните с приведенными в таблице.

Совпадение с контрольным образцом показывает правильность введения формул.

2. Введите свои данные и скопируйте формулы в нижестоящие ячейки в обозримом пространстве экрана.

3. Выделите расчетные столбцы и постройте диаграмму.

Технология построения диаграммы:

1) выделить ячейки столбца В в расчетном диапазоне вместе с заголовком;
2) выбрать команду Вставка/Диаграмма;
3) на 1-м шаге выбрать тип диаграммы — график;
4) на 2-м шаге на вкладке Ряд в поле Подписи оси X выделить расчетные ячейки столбца А без заголовка;
5) на 3-м шаге ввести название диаграммы «Рождаемость», отменить легенду;
6) на 4-м шаге выбрать расположение диаграммы;
7) построенную диаграмму скопировать в текстовый процессор.

IV этап. Анализ результатов моделирования

Оценить по диаграмме рост численности амеб.

Выводы:

1. Модель показывает, что количество клеток увеличивается в геометрической прогрессии, то есть очень быстро. При сделанном огрублении модели численность растет бесконечно.

2. В реальности рост клеток должен быть ограничен внешними факторами, влияющими на их жизнеспособность. Только на малом отрезке времени такая модель может характеризовать процесс с достаточной точностью.

3. Требуется корректировка модели с учетом естественной смертности.

МОДЕЛЬ 2. Рождаемость и смертность

I этап. Уточненная постановка задачи

Рассмотрим некоторую систему, в которой численность особей популяции зависит только от естественной рождаемости и смертности. Еды в такой системе хватает всем, экология не нарушена, жизни ничто не угрожает. Это некий «шведский социализм» или «образцовый рай». 

II этап. Разработка модели

ИНФОРМАЦИОННАЯ МОДЕЛЬ

Здесь модель характеризуется коэффициентами КР и КС, учитывающими рождаемость и смертность в течение одного периода. КР = 0,03, к примеру, означает, что в течение некоторого периода времени на каждые 100 особей рождается 3 новых (прирост за период равен 3%). Для человека периодом наблюдения может служить год, для бактерий или мух этот период значительно короче (часы, дни).

Математическая модель процесса изменения численности может быть представлена следующими уравнениями:

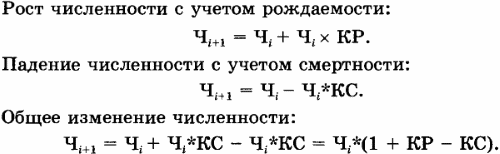
КОМПЬЮТЕРНАЯ МОДЕЛЬ

Для моделирования выберем электронные таблицы. Представим информационную модель в виде таблицы, содержащей области исходных и расчетных данных (результатов).

Введите в таблицу исходные данные, в расчетную часть — следующие формулы:

III этап. Компьютерный эксперимент

ПЛАН ЭКСПЕРИМЕНТА

ТЕСТИРОВАНИЕ

Провести тестовый расчет модели самостоятельно.

ЭКСПЕРИМЕНТ

Исследовать изменение численности популяции в течение 50 периодов в зависимости от начальной численности и коэффициентов рождаемости, смертности.

ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ

1. Компьютерное тестирование проведите самостоятельно.

2. Постройте диаграмму по результатам расчетов.

3. Определите по диаграмме, когда численность популяции увеличится вдвое.

4. Измените один из коэффициентов (рождаемости или смертности) вдвое и наблюдайте за общим изменением численности. Сделайте вывод.

5. Установите коэффициенты рождаемости и смертности равными и наблюдайте за общим изменением численности.

IV этап. Анализ результатов моделирования

По результатам экспериментов ответьте на следующие вопросы:

1. Каким должно быть сочетание КР и КС, чтобы численность:

• росла;
• убывала;
• оставалась неизменной.

2. Какие, на ваш взгляд, важные факторы не учтены в этой модели?

3. Позволяет ли данная модель сделать нижеследующие выводы:

• при КР ˂ КС популяция нежизнеспособна;
• при КР ˃ КС численность популяции экспоненциально растет, что нельзя признать реалистичным, так как интенсивный рост популяции приводит к перенаселенности и нехватке пищи, а соответственно к гибели особей;
• требуется корректировка модели с учетом влияния численности популяции на ее жизнеспособность.

МОДЕЛЬ 3. Рождаемость и смертность с учетом изменяющейся численности популяции

I этап. Уточненная постановка задачи

В моделях 1 и 2 говорилось о популяции, но она рассматривалась не как система, а как сумма отдельных особей. Это происходило потому, что в моделях не учитывались связи и взаимодействие между особями популяции и влияние среды обитания. Как правило, численность популяции зависит не только от рождаемости и смертности ее особей, но и от ограниченности пищевых и других жизненных ресурсов.

В предыдущей задаче мы вычисляли численность популяции по формуле: Ч_i+1 = Ч_i * (1 + КР - КС) = Ч_i * К, где К — обобщенный коэффициент рождаемости и смертности — константа. На самом деле, как сказано выше, этот коэффициент должен зависеть от текущей численности, то есть являться функцией от численности: f Ч_i.

Как только численность превышает некоторый предел, проявляется недостаток жизненного пространства и пищевых ресурсов и, как результат, растет смертность среди особей популяции. Такие явления наблюдаются не только среди популяций животных и насекомых, но и среди людей в тех странах, где рождаемость бесконтрольно растет. В качестве примера можно привести Китай, где законодательно ограничено число детей в семье.

Общий вид функции f Ч_i зависит от особенностей изучаемого биологического вида и окружающей его среды. Мы будем считать, что f Ч_i является линейной функцией, то есть самой простой зависимостью. Линейную функцию f Ч_i можно задать следующей формулой: f Ч_i = А * (1 - В * Ч_i).

В этой формуле величина коэффициента А отражает устойчивость вида, обитающего в благоприятных условиях. Чем выше А, тем более плодовит вид, тем выше выживаемость молодых особей.

Величина коэффициента В определяется параметрами среды обитания биологического вида (размером площади обитания, количеством пищи и т. п.).

Из формулы видно, что когда Ч_i = 1/В, то популяция вымирает.

II этап. Разработка модели

ИНФОРМАЦИОННАЯ МОДЕЛЬ

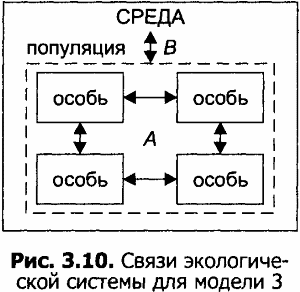
На рисунке 3.10 схематично представлены связи элементов экологической системы.

Математическая модель изменения во времени численности вида с учетом линейной зависимости обобщенного коэффициента рождаемости и смертности от численности популяции такова:

Ч_i+1 = Ч_i * f Ч_i = Ч_i * A * (1 - B * Ч_i).

КОМПЬЮТЕРНАЯ МОДЕЛЬ

Для моделирования выберем среду Рис 3.10. Связи экологиче- электронных таблиц, определив области ск°й системы для модели 3 исходных и расчетных данных. Ввести в верхнюю часть таблицы исходные данные, а в расчетную — следующие формулы:

III этап. Компьютерный эксперимент

ПЛАН ЭКСПЕРИМЕНТА

ТЕСТИРОВАНИЕ

Провести тестовый расчет модели самостоятельно.

ЭКСПЕРИМЕНТ 1

Изменяя коэффициенты A и В, проследить за характером изменения численности.

ЭКСПЕРИМЕНТ 2

Изменяя коэффициент А при неизменном В, проследить за характером изменения численности.

ЭКСПЕРИМЕНТ 3

Изменяя коэффициент В при неизменном А, проследить за характером изменения численности. Построить общую диаграмму для разных коэффициентов.

ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ

ЭКСПЕРИМЕНТ 1. Исследование изменения численности популяции для разных коэффициентов А и В

1. Рассчитайте процессы изменения численности популяции для следующих коэффициентов А и В : А = 2,0, В = 0,002. По результатам моделирования постройте диаграмму.

ЭКСПЕРИМЕНТ 2. Исследование изменения численности популяции при изменении устойчивости вида А

2. Выполните расчеты модели для разных коэффициентов А при неизменном В:

а) А = 2,5 и В = 0,001;
б) А = 2,8 и В = 0,001;
в) А = 4,5 и В = 0,001.

По результатам моделирования постройте общую диаграмму. Технология построения диаграммы для нескольких кривых:

• ввести новый набор исходных коэффициентов в ячейки В4 и В5. Модель моментально просчитается с этими данными;
• скопировать столбец В и вставить результаты в ячейки столбца С (меню Правка, команда Специальная вставка| Переключатель значения);
• повторить предыдущие пункты для следующих коэффициентов, поместив новые результаты для второй пары коэффициентов в столбец D, для третьей пары — оставить в столбце В;

• выделить блок расчетных ячеек в столбцах А, В, С и D;
• построить общую диаграмму.

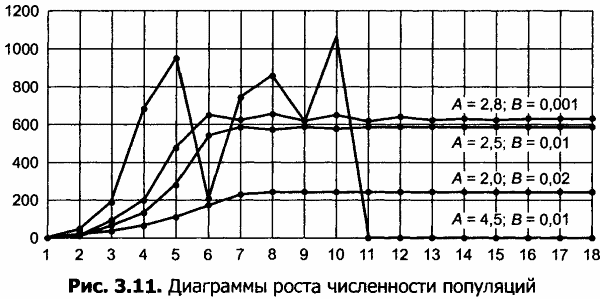
Пример построения диаграмм для различных коэффициентов А и В приведен на рисунке 3.11.

АНАЛИЗ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА

По результатам эксперимента ответить на следующие вопросы:

1. Определить по диаграммам, через сколько периодов при заданных значениях А и В численность стабилизируется.
2. Что происходит при увеличении коэффициента А?
3. Каково поведение популяции при А ˃ 3?
4. Что означают отрицательные значения численности при расчете модели с коэффициентом А = 4,5?
5. Изменить формулу для расчета численности популяции, введя функцию условия ЕСЛИ. По такой формуле вместо отрицательных значений численности в расчетную ячейку будет заноситься число 0, что соответствует полному вымиранию популяции:

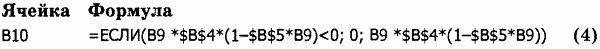
Как правило, полного вымирания не происходит, остается несколько особей, которые начинают новый виток развития. Что нужно изменить в формуле (4), чтобы смоделировать эту ситуацию?

Оформить исследование в виде отчета в текстовом процессоре, вставив соответствующие диаграммы.

ЭКСПЕРИМЕНТ 3. Исследование изменения численности популяции при изменении коэффициента среды В

Выполните расчеты и постройте общую диаграмму для разных коэффициентов В при неизменном А:

а) А = 2,0 иВ = 0,001;
б) А = 2,0 и В = 0,002;
в) А = 2,0 и В = 0,005.

АНАЛИЗ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА

По результатам эксперимента ответить на следующие вопросы:
1. Определить по диаграмме изменение численности при неизменном коэффициенте А. Объяснить это с теоретической точки зрения, изложенной при постановке задачи.

2. Что может означать прямой участок диаграммы, на котором рост численности прекращается?
3. Как можно объяснить небольшие колебания численности в ту или другую сторону на участке со стабильной численностью?

IV этап. Анализ результатов

По выводам, сделанным по результатам экспериментов, провести анализ модели и ответить на следующие вопросы:

Отражает ли модель реальную ситуацию существования популяции?
Какие дополнительные факторы можно учесть при разработке модели?

МОДЕЛЬ 4. Моделирование сосуществования двух соперничающих видов

I этап. Уточненная постановка задачи

Предыдущие модели отражали жизнь одного вида без взаимоотношений с другими. И хотя популяция и среда обитания в модели 3 были представлены как система, в природе почти невозможно представить обособленную жизнь одного вида.

Усложним модель, рассмотрев экологическую систему с двумя соперничающими видами. Пусть это будут, к примеру, белки и бурундуки. Соперничество этих видов не касается мест обитания, так как они проживают в разных местах: белки — в дуплах деревьев, а бурундуки — в норах. Но оба вида питаются плодами, орехами и насекомыми, то есть пищевые ресурсы у них общие.

В условиях соперничества двух видов за пищевые ресурсы, рождаемость и смертность каждого зависит не только от собственной численности, но также от численности другого вида. Поэтому в такой системе существуют более сложные связи и взаимодействие.

Следует заметить, что белки и бурундуки не едят друг друга, а в рассматриваемом лесу, вдобавок, не испытывают на себе зубы третьего вида — хищников, что существенно упрощает модель.

II этап. Разработка модели

ИНФОРМАЦИОННАЯ МОДЕЛЬ

На рисунке 3.12 схематично представлены связи между двумя соперничающими популяциями в экологической системе.

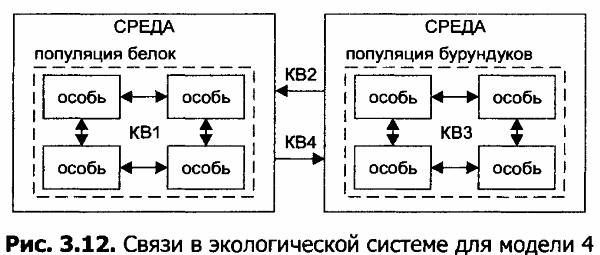
Если бы белки и бурундуки не конкурировали между собой за источники пищи, можно было бы ожидать, что изменение численности каждого вида описывалось бы соотношениями, подобными тем, что приведены в модели 3, то есть численность одного вида не влияла бы на численность другого. 

Математическая модель изменения численности по уточненному условию:

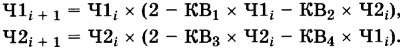
КОМПЬЮТЕРНАЯ МОДЕЛЬ

Для моделирования выберем электронные таблицы. Ввести в верхнюю часть таблицы исходные данные, а в расчетную часть — следующие формулы:

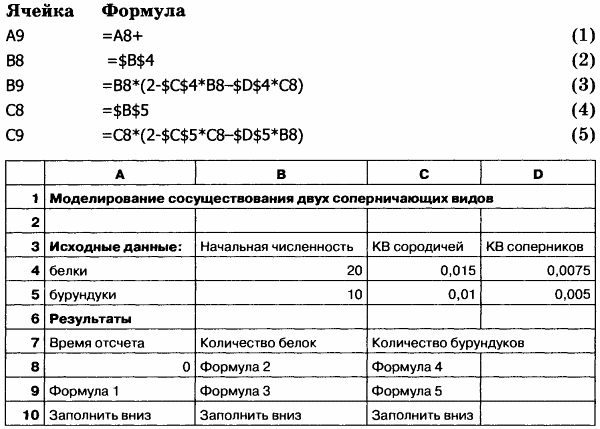
Разница в значениях коэффициентов влияния со стороны сородичей и со стороны соперников (например, для белок 0,015 и 0,0075 соответственно) показывают, что особи одного вида соперничают между собой сильнее, чем особи разных видов. Это происходит потому, что внутри вида происходит борьба за все жизненно важные ресурсы: и пищу, и места обитания, тогда как соперничество между разными видами касается только пищи. 

III этап. Компьютерный эксперимент

СОСТАВЛЕНИЕ ПЛАНА ЭКСПЕРИМЕНТА

ТЕСТИРОВАНИЕ

Провести тестовый расчет модели самостоятельно.

ЭКСПЕРИМЕНТ 1

Изменяя исходную численность популяций, следить за характером изменения численности в течение последующих периодов.

ЭКСПЕРИМЕНТ 2

Изменяя коэффициенты влияния, следить за характером изменения численности.

ЭКСПЕРИМЕНТ 3

Смоделировать экологическую систему с тремя соперничающими видами.

ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ

ЭКСПЕРИМЕНТ 1. Исследование роста популяции в зависимости от соотношения начальной численности

Рассчитать процессы изменения численности популяции для следующих начальных численностей популяций:

а) 10 белок, 10 бурундуков;
б) 10 белок, 20 бурундуков.

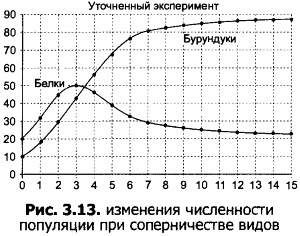
Примерный вид совместной диаграммы по результатам эксперимента приведен на рисунке 3.13.

Как видно из диаграммы, через некоторое время численность популяций в условно упрощенном лесу стабилизируется на некотором уровне. Уровень зависит как от особенностей самого вида, так и от внешних факторов, в том числе от влияния соперников.

ЭКСПЕРИМЕНТ 2. Исследование зависимости численности популяций от коэффициентов влияния

1. Рассчитайте процессы изменения численности популяций птиц (попарно). Синицы и соловьи соперничают только за пищевые ресурсы, так как гнездуются по-разному. Гуси и утки соперничают и за пищевые ресурсы, и за среду обитания, но утки более приспособлены к изменяющимся условиям среды (вспомните городские водоемы). Для расчетов используйте следующие условные коэффициенты влияния:

Проведите несколько вариантов расчетов с различными значениями начальной численности видов.

2. Постройте диаграммы по результатам эксперимента. Скопируйте их в текстовый документ для дальнейшего анализа.

ЭКСПЕРИМЕНТ 3. Исследование системы с тремя соперничающими видами

Самостоятельно смоделируйте экологическую систему с тремя соперничающими видами. Подберите коэффициенты и придумайте легенду их сосуществования.

IV этап. Анализ результатов моделирования

По результатам моделирования провести исследование влияния численности одного вида на развитие другого, для чего ответить на следующие вопросы:

1. Как влияет первоначальная разница в численности на модель?
2. Какой вид первоначально имеет преимущество в развитии?
3. Сохраняется ли это преимущество в дальнейшем?
4. Как развиваются виды, если их характеристики одинаковы?
5. Как влияет разница в коэффициентах влияния со стороны сородичей на совместное развитие видов? Какой вид получает преимущество? Что происходит с другим видом?

МОДЕЛЬ 5. Враждующие популяции

I этап. Уточненная постановка задачи

Достаточно распространенной является ситуация, когда два враждующих рода, агрессивно настроенных друг против друга, занимают одно и то же жизненное пространство. Это случается и в мире животных, и среди людей. Особенно уродливые формы приобретают такие ситуации среди Homosapiens, т. е. среди мыслящих людей. Это выливается в кровопролитные войны, в родовую ненависть с кровной местью. Попытаемся с помощью моделирования провести анализ того, что при этом происходит, и оценить разрушительное влияние вражды и войн на жизнеспособность двух враждующих видов.

II этап. Разработка модели

ИНФОРМАЦИОННАЯ МОДЕЛЬ

Эта модель может рассматриваться как развитие модели 4. Схема взаимодействия видов, таблица характеристик элементов системы, а также математическая модель изменения численности популяций полностью сохраняются. Явным отличием этой модели являются значения коэффициентов влияния. В условиях вражды обобщенные коэффициенты влияния со стороны соперников будут значительно превышать коэффициенты влияния со стороны сородичей.

КОМПЬЮТЕРНАЯ МОДЕЛЬ

Заполнить таблицу, введя в ячейки исходные данные и формулы. Формулы 1-5 соответствуют формулам, приведенным в модели 4.

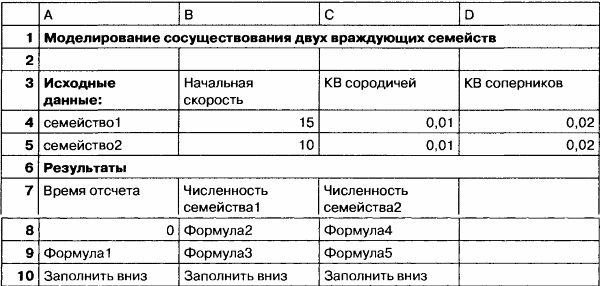
III этап. Компьютерный эксперимент

ПЛАН ЭКСПЕРИМЕНТА

ТЕСТИРОВАНИЕ

Провести тестовый расчет модели самостоятельно.

ЭКСПЕРИМЕНТ 1

Изменяя исходную численность популяций, следить за характером изменения численности в условиях вражды в течение последующих периодов.

ЭКСПЕРИМЕНТ 2

Изменяя исходную численность популяций, рассчитать процессы изменения численности семейств в условиях, когда один вид является пищей для другого вида.

ЭКСПЕРИМЕНТ 3

Смоделировать экологическую систему с тремя соперничающими видами.

ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ

ЭКСПЕРИМЕНТ 1. Исследование изменения численности видов в условиях вражды

1. Рассчитайте процессы изменения численности семейств в условиях вражды, когда влияние со стороны сородичей одинаковое (KB₁ = КВ₃ = 0,01) и со стороны соперников тоже одинаковое, но значительно сильнее (КВ₂ = КВ₄ = 0,02). Расчеты произведите для следующих начальных численностей семейств 1 и 2:

а) 15, 10;
б) 10, 10;
в) 5, 15.

2. Постройте совместную диаграмму изменения численности соперничающих видов.

Примерный вид диаграммы по результатам эксперимента приведен на рисунке 3.14. 

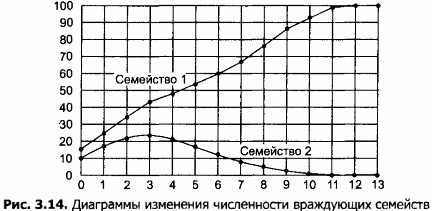
ЭКСПЕРИМЕНТ 2. Исследование изменения численности в системе «хищники — жертвы»

1. Рассчитайте процессы изменения численности популяций в условиях, когда один вид является пищей для другого. Для расчетов используйте следующие условные коэффициенты влияния:

Среди указанных коэффициентов один отрицательный (КВ₄). Это говорит о том, что рост численности жертв, являющихся пищей хищников, благотворно влияет на численность последних.

Проведите расчеты для нескольких вариантов начальной численности обеих популяций.

2. Постройте совместную диаграмму изменения численности соперничающих видов.

3. Измените коэффициенты влияния, обосновав их новые значения, и проведите расчеты.

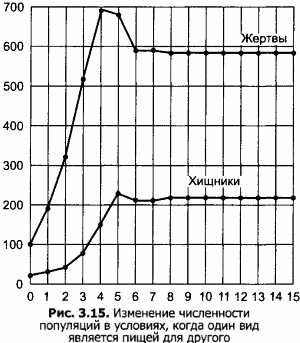
4. Постройте диаграммы по результатам эксперимента. Скопируйте их в текстовый документ для дальнейшего анализа. Примерный вид диаграммы по результатам эксперимента приведен на рисунке 3.15.

IV этап. Анализ результатов моделирования

Анализ модели провести самостоятельно. Письменно сделать выводы и обосновать их.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

3.30. Кроличья семья.

Самка кролика каждые два месяца приносит в среднем 10 крольчат. Провести расчет пополнения кроличьей семьи молодняком в течение года.

3.31. Выращивание пшеницы.

Из 1 зерна пшеницы вырастает колос, содержащий в среднем 25 семян. Вес 1 зернышка 0,1 г.

У Робинзона Крузо, попавшего на необитаемый остров, чудом сохранилось 10 зерен. Он бережно посадил их, а когда собрал урожай, то вновь посадил все до единого зернышка. В условиях жаркого тропического климата на острове можно снимать 4 урожая в год. Для того чтобы обеспечить себя хлебом до следующего урожая, надо иметь 45 кг зерна (по 0,5 кг на каждый день).

После какого урожая Робинзон первый раз смог побаловать себя вкусными хлебными лепешками? Сколько килограммов семян надо сажать, чтобы получить урожай, достаточный и для прокорма до следующего урожая и для посадки? Для упрощения задачи не будем учитывать непогоду, пожары, засуху и прочие ненастья. А также будем считать, что все посаженные зерна всходят.