Урок 20
Моделирование в электронных таблицах
Моделирование случайных процессов
Случай является неотъемлемой частью нашей жизни. Если случай помог нам в чем-то, мы говорим — повезло, если оказался не в нашу пользу, мы сокрушаемся — что за судьба! Многие ученые посвятили свой талант изучению закономерностей случайных событий. Знание законов случайностей может быть полезным в разных сферах: от определения вероятности некоторого события, например выигрыша в лотерею, до использования статистических закономерностей в научных опытах. Ниже будут смоделированы ситуации, которые в теории вероятности получили название «случайных блужданий».
Представьте себя на длинной прямой дороге. Вы бросаете монету. Если выпал «орел», то делаете шаг вперед, если «решка» — шаг назад. Как далеко уведет вас такое одномерное (в одном направлении) блуждание?
ЗАДАЧА 3.32. Бросание монеты
I этап. Постановка задачи
ОПИСАНИЕ ЗАДАЧИ
У вас есть 10 монет. Вы хотите увеличить свой капитал в два раза, испытав заодно и свою судьбу. Суть игры проста. Играя с маклером, вы делаете ставку и бросаете монету. Если выпадет «орел», маклер выдает вам сумму вашей ставки, в противном случае — вы ему отдаете эту сумму. Ставка может быть любой: от 1 до 10 монет. Вы можете назначить самую большую ставку в 10 монет, и тогда за один бросок выяснится, «сорвали» ли вы банк или, наоборот, обанкротились. Опытные игроки действуют более осторожно, начиная с маленькой ставки.
Удвоение начального капитала или банкротство приводит к незамедлительному прекращению этого сеанса игры и расчету. Игра может продолжиться по вашему усмотрению.
ЦЕЛЬ МОДЕЛИРОВАНИЯ
Моделируя возможные игровые ситуации, в частности, варьируя ставки в данной игре, выяснить, какая тактика чаще приводит к результату (положительному или отрицательному).
Предупредить потенциальных игроков о степени риска и невозможности обогащения за счет азартных игр.
ФОРМАЛИЗАЦИЯ ЗАДАЧИ
Ответим на следующие вопросы:

II этап. Разработка модели
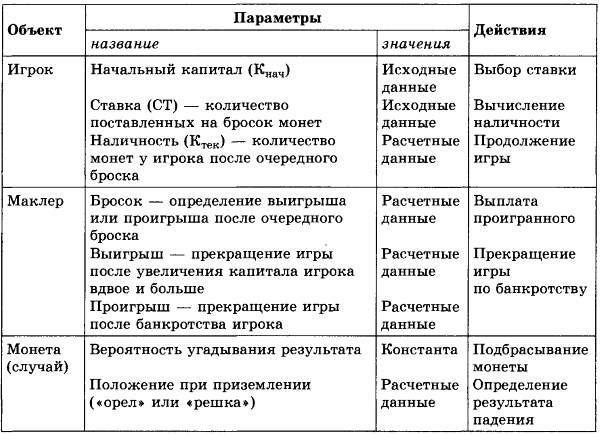
ИНФОРМАЦИОННАЯ МОДЕЛЬ
Здесь моделируется игра. Игра — это процесс, в котором участвуют три объекта: игрок, маклер и «его Величество случай», который в данной игре представлен монетой. Маклер определяет проигрыш или выигрыш игрока, выплачивает выигрыш.
Математическая модель процесса складывается из следующих рассуждений.
Имитировать результат падения монеты можно с помощью функции СЛЧИС(). Эта функция выдает случайные числа х в диапазоне 0 ≤ х ˂ 1. Поскольку вероятность выпадения той или иной стороны «половина на половину», то, если СЛЧИС() ˂ 0,5, то результат «орел» (1), в противном случае — «решка» (0).
Формула падения монеты при броске имеет следующий вид:
Бросок = ЕСЛИ(СЛЧИС() ˂ 0,5; 1; 0),
здесь «1» на выходе функции означает, что игрок угадал, то есть выпал «орел», а «О» — не угадал, то есть выпала «решка».
Формула изменения наличности игрока:
Наличность = ЕСЛИ(Бросок=1; Наличность+Ставка; Наличность-Ставка)
Формула определения выигрыша:
Выигрыш = ЕСЛИ(Наличность ˂ 2*Нач.Капитал;"-"; "банк")
здесь выдается сообщение «банк» при увеличении наличности вдвое или больше, что является условием прекращения игры.
Функция определения проигрыша:
Проигрыш = ЕСЛИ(Наличность ˃ 0; "банкрот")
здесь выдается сообщение «банкрот» по окончании наличности, что также является условием прекращения игры.
КОМПЬЮТЕРНАЯ МОДЕЛЬ
Для моделирования выберем среду электронной таблицы. В этой среде информационная и математическая модель объединяются в таблицу, которая содержит три области:
► исходные данные;
► расчетные данные (результаты);
► статистика по экспериментам.
Ввести в таблицу исходные данные.
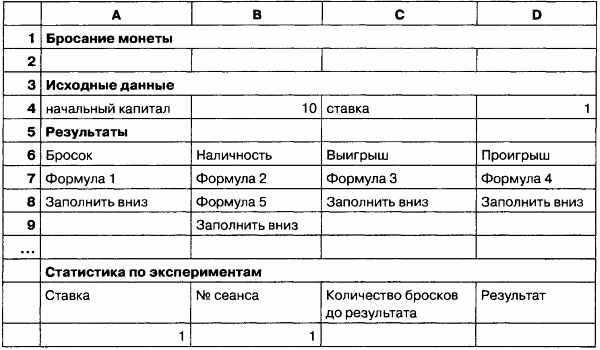
Ввести в расчетную часть следующие формулы:

III этап. Компьютерный эксперимент
ПЛАН ЭКСПЕРИМЕНТА
ТЕСТИРОВАНИЕ
Проверить правильность ввода формул.
ЭКСПЕРИМЕНТ 1
Исследовать выпадение «орла» и «решки» в течение сеанса игры.
ЭКСПЕРИМЕНТ 2
Собрать статистические данные о выигрыше и проигрыше в течение нескольких сеансов игры с различными значениями ставок и исследовать их.
ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ
ТЕСТИРОВАНИЕ
Введите в таблицу контрольные исходные данные и расчетные формулы в первую строку. Результаты сравнить с приведенными в таблице.
Видим уменьшение наличности на величину ставки. Если в столбце Бросок выпала «1» («орел»), данные в остальных столбцах должны быть следующими:

Если в столбце Бросок выпал «О» («решка»), данные в остальных столбцах должны быть следующими:

Видим увеличение наличности на величину ставки. Сравнение с контрольным образцом показывает правильность введения формул.
ЭКСПЕРИМЕНТ 1. Имитация одного сеанса игры для определенной ставки
1. Скопируйте формулы в нижестоящие ячейки в обозримом пространстве экрана (примерно 20 бросков). Таким образом вы моделируете сразу весь сеанс игры — 20 бросков. Можно «растянуть» удовольствие и копировать формулы только в один нижестоящий ряд, имитируя один бросок монеты. Но, учитывая то, что требуется набрать некоторую статистику для выводов, эксперимент сознательно убыстряется. Появление в столбце Выигрыш сообщения «банк» означает удвоение наличности, а в столбце Проигрыш сообщения «банкрот» нулевую наличность. И то и другое приводит к концу сеанса игры. Нижестоящие результаты игнорируются. Сеанс игры считается законченным.
2. Следующий сеанс игры проводится в тех же ячейках путем обновления данных 1-го столбца, для чего формулу в ячейке А7 надо заново скопировать в нижестоящие ячейки.
3. Соберите статистику игры. Для этого в свободной области электронной таблицы запишите результаты 10-20 сеансов игры в следующем виде:
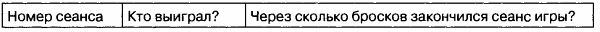
По собранной статистике ответьте на вопросы:
♦ Кто чаще выигрывает: казино или игрок?
♦ Сколько в среднем бросков надо сделать до окончания игры? ЭКСПЕРИМЕНТ 2. Имитация игры с разными ставками Измените размер ставки на один бросок (4, 7 и 10 монет). Сделайте 20 бросков. Игра может закончиться раньше, а может и не закончиться.
Проведите 10 сеансов игры для каждой ставки.
Соберите статистику игры. Для этого в свободной области электронной таблицы запишите результаты 10 сеансов игры в следующем виде:

В столбце Результат возможны следующие значения:
♦ выигрыш (при появлении значения «банк»);
♦ проигрыш (при появлении значения «банкрот»);
♦ нет (нерезультативная игра).
IV этап. Анализ результатов моделирования
На основе области «Статистика» сделать выводы по поводу ставки в одну монету; других ставок. Выбрать и обосновать собственную тактику игры (ставку).
ЗАДАЧА 3.33. Игра в рулетку
I этап. Постановка задачи
ОПИСАНИЕ ЗАДАЧИ
Казино процветают из-за того, что у владельца всегда есть некоторое преимущество перед игроком. Например, в одном из вариантов рулетки колесо имеет 38 лунок: 36 пронумерованы и разбиты на черный и красный цвет, а две оставшиеся имеют № 0 и 00 и выкрашены зеленым. Игрок, ставя на красное или черное, имеет на выигрыш 18 шансов из 38, а на то, что он проиграет — 20 шансов из 38.
Повторить эксперимент задачи 3.32, считая, что у вас есть некоторое число фишек и вы хотите увеличить свой капитал в 2 раза. Если колесо остановилось на выбранной вами цифре, ваш капитал увеличится на величину ставки, в противном случае ставка уйдет в доход казино.
ЦЕЛЬ МОДЕЛИРОВАНИЯ
Моделирование возможных игровых ситуаций и выработка тактики, чаще приводящей к результату (положительному или отрицательному).
Предостережение излишне азартным игрокам.
ФОРМАЛИЗАЦИЯ ЗАДАЧИ
Проведем формализацию задачи в виде поиска ответов на следующие вопросы:


II этап. Разработка модели
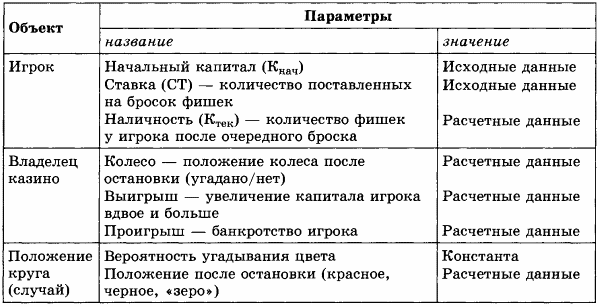
ИНФОРМАЦИОННАЯ МОДЕЛЬ
Здесь моделируется игра. Игра — это процесс, в котором участвуют три объекта: игрок, владелец казино и случай, представленный в данной игре рулеткой. Случай характеризуется угадыванием или нет того, какой цвет выпал на колесе, и имеет два значения: «угадал» (1) или «не угадал» (0).
Математическая модель процесса складывается из следующих рассуждений.
Имитировать ставку игрока с помощью функции СЛЧИС() бессмысленно, так как это зависит только от него. Игрок может ставить всегда на красный цвет, или всегда на черный, или через раз...
Имитировать результат поворота колеса можно с помощью функции СЛЧИС(), которая выдает числа в диапазоне 0 ≤ х ˂ 1. Вероятность угадывания цвета составляет по условию задачи 18/38, что равно 0,47. Число 0,47 делит диапазон случайных чисел на две неравные части. Попадание в меньшую часть диапазона означает угадывание результата (у него меньшая вероятность), в большую — неудачу (с большей вероятностью). Эту ситуацию можно описать следующей формулой:
Колесо = ЕСЛИ(СЛЧИС()˂0,47; 1; 0).
Формулы изменения наличности, а также прекращения игры в результате увеличения наличности вдвое или банкротства аналогичны приведенным в задаче 3.32.
КОМПЬЮТЕРНАЯ МОДЕЛЬ
Для моделирования выберем среду электронной таблицы. В этой среде информационная и математическая модель объединяются в таблицу, которая содержит три области:
► исходные данные;
► расчетные данные (результаты);
► статистика по экспериментам.
Ввести в таблицу исходные данные:

Ввести в рассчетную часть следующие формулы:

III этап. Компьютерный эксперимент
ПЛАН ЭКСПЕРИМЕНТА
ТЕСТИРОВАНИЕ
Проверить правильность ввода формул.
ЭКСПЕРИМЕНТ 1
Исследовать выпадение выигрыша в течение одного сеанса игры.
ЭКСПЕРИМЕНТ 2
Собрать статистические данные о выигрыше и проигрыше в течение нескольких сеансов игры с различными значениями ставок и исследовать их.
ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ
ТЕСТИРОВАНИЕ
Введите в таблицу контрольные исходные данные и расчетные формулы в первую строку. Результаты сравните с приведенными в таблице.
Если в столбце Колесо результат получился равным 1, данные в остальных столбцах должны быть следующими:

Видим увеличение наличности на величину ставки.
Если в столбце Колесо результат получился равным 1, данные в остальных столбцах должны быть следующими:

Видим уменьшение наличности на величину ставки. Сравнение с контрольным образцом показывает правильность введения формул.
ЭКСПЕРИМЕНТ 1. Имитация одного сеанса игры для определенной ставки
1. Скопируйте формулы в нижестоящие ячейки в обозримом пространстве экрана (примерно 20 поворотов колеса). Таким образом вы моделируете сразу весь сеанс игры. Появление в столбце Выигрыш сообщения «банк» означает удвоение наличности, а в столбце Проигрыш сообщения «банкрот» — нулевую наличность. И то и другое приводит к концу сеанса игры. Нижестоящие результаты игнорируются. Сеанс игры считается законченным.
2. Следующий сеанс игры проведите в тех же ячейках путем обновления данных 1-го столбца, для чего формулу в ячейке А7 заново скопируйте в нижестоящие ячейки
3. Соберите статистику игры. Для этого в свободной области таблицы запишите результаты 10—20 сеансов игры в следующем виде:

По собранной статистике ответьте на вопросы:
♦ Кто чаще выигрывает — казино или игрок?
♦ Сколько в среднем поворотов колеса надо сделать до окончания игры?
ЭКСПЕРИМЕНТ 2. Набор статистики для самостоятельно выбранной ставки
1. Измените размер ставки (4, 7 или 10 монет).
2. Сделайте 20 поворотов колеса. Игра может закончиться раньше, а может и не закончиться.
3. Проведите 10 сеансов игры для каждой ставки.
4. Соберите статистику игры. Для этого в свободной области электронной таблицы запишите результаты 10 сеансов игры в следующем виде:

В столбце Результат возможны следующие значения:
♦ выигрыш (при появлении значения «банк»);
♦ проигрыш (при появлении значения «банкрот»);
♦ нет (нерезультативная игра).
IV этап. Анализ результатов
Проанализировать данные области «Статистика». Сравнить количество выигрышей и проигрышей. Просуммировать столбцы выигрышей и проигрышей и сделать выводы.
ЗАДАЧА 3.34. Игра в кости
I этап. Постановка задачи
ОПИСАНИЕ ЗАДАЧИ
Два игрока бросают по две игровые кости.
Сумма очков, выпавших на двух игровых костях, накапливается. Игра прекращается, когда один из игроков достигает суммы 101.
Игра повторяется до трех побед.
ЦЕЛЬ МОДЕЛИРОВАНИЯ
Создание игровой модели, основанной на случайных событиях.
ФОРМАЛИЗАЦИЯ ЗАДАЧИ
Проведем формализацию задачи в виде поиска ответов на следующие вопросы:


II этап. Разработка модели
ИНФОРМАЦИОННАЯ МОДЕЛЬ

Математическая модель процесса складывается из следующих рассуждений.
На игровой кости имеется 6 граней с количеством точек от 1 до 6.
Модель, имитирующая бросание двух костей одним игроком:
К1=ЦЕЛОЕ(1+6*СЛЧИС())
К2=ЦЕЛОЕ(1+6*СЛЧИС())
Случайные значения суммируются. Суммы бросков по каждому игроку накапливаются в отдельных столбцах Сумма первого и Сумма второго и анализируются после каждого броска в столбце Результат:
ЕСЛИ(ИЛИ ("Сумма первого"˃101; "Сумма второго"˃101); "конец игры";"-").
Здесь, когда обе суммы меньше 101, в столбец записывается «-», а при превышении хотя бы одним игроком порога в столбец записывается «конец игры». Кто победил, можно определить по соседним столбцам.
Игра прекращается при появлении сообщения «конец игры» в столбце Результат.
КОМПЬЮТЕРНАЯ МОДЕЛЬ
Для моделирования использовать среду табличного процесссора. Моделирование выполнить самостоятельно.
Можно имитировать течение игры с партнером, по очереди копируя формулы только в один ряд нижестоящих ячеек, что соответствует одному броску пары костей.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
3.35. Лотерея «Спортлото».
Кто из вас не знает лотерею «Спортлото»? Существует две распространенных тактики:
• зачеркивать в билетах одну и ту же комбинацию из «счастливых» чисел;
• бросать кубик и из количества точек на верхней грани составлять набор чисел.
Смоделируйте серию игр «5 из 36», организовав эксперименты и с одной, и с другой тактикой.
Для получения случайных чисел в пределах от 1 до 36 используйте следующую математическую модель:
К=ЦЕЛ0Е(1+36*СЛЧИС())
Наберите статистику. Сделайте выводы.

