Уроки 4 - 5
Сжатие данных без потерь
(§3. Сжатие данных)

Содержание урока

Основные понятия

Алгоритм RLE

Префиксные коды

Алгоритм Хаффмана

Сжатие с потерями

Выводы

Вопросы и задания

Задачи

Префиксные коды

Вспомните азбуку Морзе, в которой для уменьшения длины сообщения используется неравномерный код — часто встречающиеся буквы (А, Е, М, Н, Т) кодируются короткими последовательностями, а редко встречающиеся — более длинными. Такой код можно представить в виде структуры, которая называется деревом (вспомните дерево каталогов).

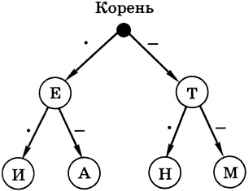
Рис. 1.2

На рисунке 1.2 показано неполное дерево кода Морзе, построенное только для символов, коды которых состоят из одного и двух знаков (точек и тире). Дерево состоит из узлов (большая чёрная точка и кружки с символами алфавита) и соединяющих их направленных рёбер, стрелки указывают направление движения. Верхний узел (в который не входит ни одна стрелка) называется корнем дерева. Из корня и из всех промежуточных узлов (кроме конечных узлов — листьев) выходят две стрелки, левая помечена точкой, а правая — знаком «тире». Чтобы найти код символа, нужно пройти по стрелкам от корня дерева к нужному узлу, выписывая метки стрелок, по которым мы переходим. В дереве нет циклов (замкнутых путей), поэтому кодовое слово для каждого символа определяется единственным образом. По этому дереву можно построить такие кодовые слова:

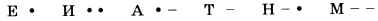
Это неравномерный код, в нём символы имеют коды разной длины. При этом всегда возникает проблема разделения последовательности на отдельные кодовые слова. В коде Морзе она решена с помощью символа-разделителя — паузы. Однако можно не вводить дополнительный символ, если выполняется условие Фано: ни одно из кодовых слов не является началом другого кодового слова. Это позволяет однозначно раскодировать сообщение в реальном времени, по мере получения очередных символов.

Префиксный код — это код, в котором ни одно кодовое слово не является началом другого кодового слова (условие Фано).

Для использования этой идеи в компьютерной обработке данных нужно было разработать алгоритм построения префиксного кода. Впервые эту задачу решили, независимо друг от друга, американские математики и инженеры Клод Шеннон и Роберт Фано (код Шеннона—Фано). Они использовали избыточность сообщений, состоящую в том, что символы в тексте имеют разные частоты встречаемости. В этом случае для построения кода нужно читать данные исходного файла два раза: на первом проходе определяется частота встречаемости каждого символа, затем строится код с учётом этих данных, и на втором проходе символы текста заменяются на их коды.

Пусть, например, текст состоит только из букв «О», «Е», «Н», «Т» и пробела. Известно, сколько раз они встретились в тексте: пробел — 179, О — 89, Е — 72, Н — 53 и Т — 50 раз. Делим символы на 2 группы так, чтобы общее количество найденных в тексте символов первой группы было примерно равно общему количеству символов второй группы. В нашем случае лучший вариант — это объединить пробел и букву Т в первую группу (сумма 179 + 50 = 229), а остальные символы — во вторую (сумма 89 + 72 + 53 = 214).

Символы первой группы будут иметь коды, начинающиеся с 0, а остальные — с 1. В первой группе всего два символа, у одного из них, например у пробела, вторая цифра кода будет 0 (и полный код 00), а у второго — 1 (код буквы Т — 01) .

Во второй группе три символа, поэтому продолжаем деление на две группы, примерно равные по количеству символов в тексте. В первую выделяем одну букву, которая чаще всего встречается — это буква О (её код будет 10), а во вторую — буквы Е и Н (они получают коды 110 и 111). Код Шеннона-Фано, построенный для этого случая, можно нарисовать в виде дерева (рис. 1.3).

Символ на этой схеме обозначает пробел.

Рис. 1.3

Легко проверить, что для этого кода выполняется условие Фано. Это можно сразу определить по построенному дереву. В нём все символы располагаются в листьях, а не в промежуточных узлах. Это значит, что «по пути» от корня дерева до любого символа никаких других символов в промежуточных узлах не встречается (сравните с деревом кода Морзе).

Для раскодирования очередного символа последовательности мы просто спускаемся от корня дерева, выбирая левую ветку, если очередной бит — 0, и правую, если этот бит равен 1. Дойдя до листа дерева, мы определяем символ, а затем снова начинаем с корня дерева, чтобы раскодировать следующий символ, и т. д. Например, пусть получена последовательность

01100110001101111001.

Результат ее раскодирования — «ТОТО ЕНОТ».

Следующая страница Алгоритм Хаффмана

Cкачать материалы урока