Урок 33
Уточнение понятие алгоритма. Универсальные исполнители
§34. Уточнение понятия алгоритма
Содержание урока
Зачем нужно определение алгоритма?
Машина Тьюринга
Машина Тьюринга

Первым предложил универсальный исполнитель английский математик Алан Тьюринг. Придуманное им воображаемое устройство состоит из трёх частей:
• бесконечной ленты, разделённой на ячейки;
• каретки (читающей и записывающей головки);
• программируемого автомата.
Программируемый автомат управляет кареткой, посылая ей команды в соответствии с заложенной в него сменяемой программой. Лента выполняет роль памяти компьютера, автомат — роль процессора, а каретка служит для ввода и вывода данных. Такое устройство называют машиной Тьюринга.
Теоретически лента в машине Тьюринга бесконечна, однако в каждый момент времени работы А. Тьюринг машины используется лишь конечная её часть.
Каретка в любой момент времени находится над одной ячейкой, автомат может читать и изменять содержимое этой ячейки, которая называется текущей (рабочей) ячейкой (рис. 5.2).
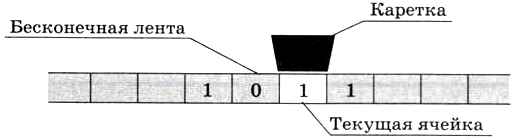
Рис. 5.2
В каждую ячейку ленты можно записать один любой символ, принадлежащий выбранному алфавиту. Любой алфавит обязательно содержит пробел (пустой символ, соответствующий «чистым» участкам ленты), который мы будем обозначать знаком ☐. Алфавит обычно обозначается буквой А, а его элементы — строчными буквами а с индексами: А = (а1, а2, ..., аN}. Например, алфавит машины Тьюринга, работающей с двоичными числами, задаётся в виде А = {0, 1, ☐}.
Непрерывную цепочку символов на ленте называют словом. На рисунке 5.2 лента содержит слово «1011», которое можно воспринимать как двоичное число.
Автоматом называют устройство, работающее без участия человека. Автомат в машине Тьюринга имеет несколько состояний и при определённых условиях переходит из одного состояния в другое. Состояние автомата определяет ту промежуточную задачу, которую решает автомат в данный момент. Это напоминает состояния человека: ночью он спит (состояние 1), утром встаёт и умывается (состояние 2), завтракает (состояние 3), идёт на работу (состояние 4) и т. д.
Множество всех состояний автомата обозначается буквой Q, а его элементы — строчными буквами q с индексами: Q = {q1, q2, ..., qM}. Принято, что в начальный момент машина Тьюринга находится в состоянии q1.
Особое состояние q0 — это состояние останова. Если машина переходит в это состояние, выполнение программы сразу останавливается.
Автомат управляется программой. Во время каждого шага программы автомат выполняет последовательно три действия:
1) изменяет символ в рабочей ячейке на другой (или оставляет без изменений);
2) перемещает каретку влево или вправо (или оставляет на месте);
3) переходит в другое состояние (или остаётся в прежнем состоянии).
Поэтому при составлении программы для каждой пары (символ, состояние) нужно определить три параметра: символ ai из выбранного алфавита А, направление перемещения каретки (← — влево, → — вправо, точка — нет перемещения) и новое состояние автомата qk. Например, команда 1 ← q2 обозначает «заменить символ на 1, переместить каретку влево на 1 ячейку и перейти в состояние q2».
 Пример 1. На ленте записано число в двоичной системе счисления. Каретка находится где-то над числом. Требуется увеличить число на единицу.
Пример 1. На ленте записано число в двоичной системе счисления. Каретка находится где-то над числом. Требуется увеличить число на единицу.
Для того чтобы построить машину Тьюринга, нужно:
• определить алфавит машины Тьюринга А;
• выделить простейшие подзадачи и определить набор возможных состояний Q; задать начальное состояние qx и конечное состояние q0 (в котором машина останавливается);
• составить программу, т. е. для каждой пары (ai, qk) определить команду, которую должен выполнить автомат.
Как мы уже выяснили, алфавит машины Тьюринга, работающей с двоичными числами, включает символы 0, 1 и пробел: А = {0, 1, ☐}. Определим возможные состояния (разобьём задачу на элементарные подзадачи):
1) q1 — автомат ищет правый конец слова (числа) на ленте;
2) q2 — автомат увеличивает число на 1, проходя его справа налево, и останавливается, закончив работу.
Теперь займёмся программой. На первом этапе, когда автомат ищет конец слова, его работа может быть описана так:
1) если в рабочей ячейке записана цифра 0, переместиться вправо;
2) если в рабочей ячейке записана цифра 1, переместиться вправо;
3) если в рабочей ячейке пробел, переместить каретку влево и перейти в состояние q2.
Тогда действия автомата в состоянии qx можно представить в виде таблицы, где в заголовках строк записываются символы алфавита, а в заголовках столбцов — состояния (рис. 5.3).
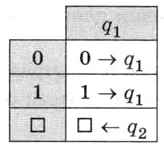
Рис. 5.3
Заметим, что во всех случаях символ под кареткой не меняется. Кроме того, состояние меняется только в последней ячейке. Поэтому для упрощения записи не будем указывать в таблице то, что остаётся без изменений. Так, на наш взгляд, более кратко и понятно (рис. 5.4).
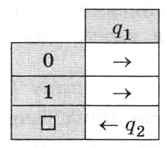
Рис. 5.4
Второй этап — увеличение двоичного числа на единицу. Это можно сделать следующим способом (вспомните тему «Системы счисления»):
1) если в рабочей ячейке записана цифра 0, записать в неё 1 и стоп;
2) если в рабочей ячейке записана цифра 1, выполнить перенос в старший разряд — записать в ячейку 0 и переместиться влево;
3) если в рабочей ячейке пробел, записать в неё 1 и стоп.
Для того чтобы остановить работу машины Тьюринга, нужно перевести её в состояние останова q0. Теперь можно добавить в таблицу столбец, соответствующий состоянию q2 (рис. 5.5).

Рис. 5.5
Построенная полная таблица (см. рис. 5.5) — это и есть программа для машины Тьюринга. Обратите внимание, что мы разбили исходную задачу на подзадачи, для каждой из них составили программу, а потом их соединили. Две подзадачи связаны через ячейку (☐, q1), в которой состояние автомата изменяется на q2. В данном простейшем случае в каждом из двух алгоритмов было использовано только одно состояние, но это не обязательно — можно таким же способом соединять и более сложные алгоритмы. Если алгоритмы А и Б можно запрограммировать на машине Тьюринга, то и любую их комбинацию тоже можно запрограммировать.
Тьюринг предположил, что:
 Любой алгоритм (в интуитивном смысле этого слова) может быть представлен как программа для машины Тьюринга.
Любой алгоритм (в интуитивном смысле этого слова) может быть представлен как программа для машины Тьюринга.
Это утверждение в теории алгоритмов известно как тезис Чёрча-Тьюринга.
Машина Тьюринга может быть строго задана с точки зрения математики. Алфавит А и набор возможных состояний Q могут быть записаны в виде множеств, а программа — в виде пятёрок вида (ai, qk, aj, dik, qm), задающих команду «если машина находится в состоянии qk и в рабочей ячейке записан символ аi, то записать в рабочую ячейку символ аj, сместиться в направлении dik и перейти в состояние qm». Например, приведённая выше программа увеличения двоичного числа на 1, записанная в виде таких пятёрок, выглядит так:
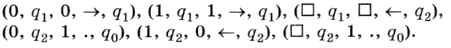
Эта машина — математический объект, и данное на её основе определение алгоритма может использоваться для доказательств. Едва ли можно применить машину Тьюринга для решения практических задач, но эта простая модель алгоритма очень удобна для проведения теоретических исследований. В отличие от интуитивного определения алгоритма новое определение не содержит таких неопределённых понятий, как «инструкция», «исполнитель», «решение задачи». Таким образом, формальное определение слова «алгоритм» (по Тьюрингу) выглядит так: алгоритм — это программа для машины Тьюринга.
Следующая страница  Машина Поста
Машина Поста

