Урок 34
§36. Сложность вычислений
(§36. Сложность вычислений)

Содержание урока

Что такое сложность вычислений?

Примеры

Что такое асимптотическая сложность?

Алгоритмы поиска

Алгоритмы сортировки

Вопросы и задания

Задачи

Алгоритмы поиска

Сравним вычислительную сложность двух наиболее известных алгоритмов поиска.

Пример 4 (линейный поиск). Дан массив, в котором элементы расположены в произвольном порядке. Требуется найти в нём заданное значение X или сообщить, что его нет.

Решение этой задачи сводится к последовательному просмотру всех элементов массива:

В этом алгоритме число сравнений (в худшем случае) равно Т(n) = n, поэтому он имеет линейную сложность.

Пример 5 (двоичный поиск). Дан массив, в котором элементы упорядочены по возрастанию. Требуется найти в нём заданное значение X или сообщить, что его нет.

По сравнению с предыдущей задачей, элементы массива отсортированы, и это ускоряет решение, потому что можно применить метод двоичного поиска (дихотомии):

Попробуем определить, сколько раз выполняется основной цикл при двоичном поиске. Сначала ширина интервала поиска — все n элементов массива. На каждом шаге этот интервал делится на 2, процесс завершается, когда левая и правая границы интервала совпадут. Предположим, что число элементов — это целая степень двойки, т. е. n = 2^m. Тогда за m шагов ширина интервала сужается до 1, а на следующем шаге его границы совпадут, и цикл закончится. Таким образом, количество шагов цикла равно m + 1. Из равенства n = 2^m получаем m = log₂n, так что

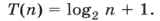
Например, при n = 2¹⁶ линейный поиск потребует в худшем случае 2¹⁶ = 65 536 сравнений, а двоичный — всего 16 + 1 = 17 сравнений.

Таким образом, алгоритм двоичного поиска имеет асимптотическую сложность O(logn). Основание логарифма обычно не указывают, потому что выражения log_an и log_bn различаются на постоянный множитель (который можно включить в постоянную с):

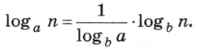
Можно ли сказать, что алгоритм двоичного поиска лучше алгоритма линейного поиска? Нет! Ведь алгоритм линейного поиска применим к любым массивам данных, а алгоритм двоичного поиска — только к упорядоченным (отсортированным). А если мы сначала отсортируем массив, а потом применим к нему двоичный поиск, то общее время работы будет больше, чем при линейном поиске.

Ситуация меняется, если нам нужно многократно выполнять операцию поиска для одних и тех же данных (так, как правило, бывает при работе с базами данных). Тогда имеет смысл заранее отсортировать массив (применить предварительную обработку данных), а затем, используя двоичный поиск, экономить время при каждом новом поисковом запросе.

Следующая страница Алгоритмы сортировки

Cкачать материалы урока