Урок 35
Доказательство правильности программ
(§37. Доказательство правильности программ)
Содержание урока
Как доказать правильность программы?
Как доказать правильность программы?
Как правило, программист разрабатывает программу на заказ, и от него требуется не только написать код, но и убедиться, что код работает правильно, т. е. в соответствии с требованиями заказчика.
Очевидно, что если программа выдаёт неверный результат хотя бы для одного варианта входных данных, можно сразу сказать, что она некорректна, т. е. содержит ошибки.
Сложнее доказать правильность программы — убедиться, что она выдает верные результаты при любых допустимых входных данных. Программисты-практики для решения этой задачи используют тестирование: проверяют работу программы с помощью набора тестовых данных, для которых известен правильный результат. Если полученный результат не совпадает с заданным, выполняется отладка программы, т. е. поиск и исправление ошибок.
Однако, как писал нидерландский учёный, один из создателей современного программирования, «отладка может показать лишь наличие ошибок и никогда — их отсутствие». В результате можно гарантировать верную работу программы только при тех данных, которые использовались в контрольных тестах.
Кроме того, неясно, как определить, что все ошибки выявлены и нужно завершить отладку.
Пример 1. Рассмотрим следующую программу для выбора максимального из трёх значений, записанных в переменных а, b и с:
если а > b то М:=а иначе М:=b все
если b > с то М:=b иначе М:=с все
Проверяя её на тестах
(а,b,с) = (1,2,3), (1,3,2), (2,1,3) и (2,3,1),
мы во всех этих случаях получаем в переменной М верный ответ 3. Однако это не означает, что программа правильная, так как существует контрпример (3,2,1): для этого набора входных данных в переменной М в результате оказывается число 2.
Чтобы быть уверенными в том, что программа работает правильно при любых допустимых исходных данных, применяют методы доказательного программирования: для каждого блока программы составляют требования к входным и выходным данным и строго доказывают, что программа всегда работает верно.
К сожалению, доказывать правильность программ не так просто, и в таких доказательствах тоже возможны ошибки. Однако при этом автор должен глубоко разобраться в алгоритме и его «подводных камнях», и часто при этом обнаруживаются ошибки, которые могли бы проявиться уже после выпуска программы в свет.
На практике редко доказывают правильность всей программы в целом. В то же время очень полезно доказывать правильность отдельных блоков (циклов, процедур и функций) для уменьшения количества «необъяснимых» ошибок и сокращения времени отладки.
Покажем метод доказательства правильности программы на простом примере.
Пример 2. Требуется доказать, что после выполнения следующей программы значения переменных а и b меняются местами:
b:=a+b | 1 a:=b-a | 2 b:=b-a | 3
Предполагается, что сумма исходных чисел не приводит к переполнению разрядной сетки. Для удобства операторы программы пронумерованы.
Обозначим начальные значения переменных а и b через а0 и b0. После выполнения оператора 1 в переменной b будет записано значение а0 + b0. Оператор 2 записывает в переменную а значение
b - a = a0 + b0 - a0 = b0.
В результате выполнения оператора 3 получаем новое значение переменной b, равное
b - a = a0 + b0 - b0 = a0.
Таким образом, в результате выполнения программы переменные а и b будут равны b0 и а0 соответственно, что и требовалось доказать. Поэтому приведённая программа правильная.
Пример 3. Попробуем доказать или опровергнуть правильность уже встречавшейся ранее программы для выбора максимального из трёх значений, записанных в переменных а, b и с:
если а > b то М:=а иначе М:=b все |1
если b > с то М:=b иначе М:=с все |2
Анализируя строку 2, выясняем, что в ней значение переменной М всегда будет изменено, т. е. результат работы первой строки программы стирается, и
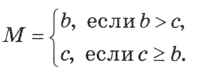
Конечно, эта величина не совпадает с определением максимального значения из а, b и с. Таким образом, программа неправильная: она выдает неверное значение, если максимальное из трёх чисел хранилось в переменной а. Контрпример мы уже приводили: (3,2,1).
Следующая страница 
Алгоритм Евклида
Cкачать материалы урока
