Уроки 47 - 49
Графы. Основные понятия
(§44. Графы)
Содержание урока
«Жадные» алгоритмы. Задача 1
«Жадные» алгоритмы. Задача 1
Задача 1. Известна схема дорог между несколькими городами. Числа на схеме (рис. 6.25) обозначают расстояния (дороги не прямые, поэтому неравенство треугольника может нарушаться). Нужно найти кратчайший маршрут из города А в город F.
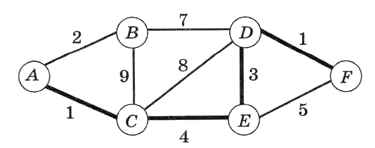
Рис. 6.25
Первая мысль, которая приходит в голову: на каждом шаге выбирать кратчайший маршрут до ближайшего города, в котором мы ещё не были. Для заданной схемы на первом этапе едем в город С (длина 1), далее — в Е (длина 4), затем в D (длина 3) и, наконец, в F (длина 1). Общая длина маршрута равна 9.
Алгоритм, который мы применили, называется «жадным». Он состоит в том, чтобы на каждом шаге многоходового процесса выбирать наилучший в данный момент вариант, не думая о том, что впоследствии этот выбор может привести к худшему решению.
Для данной схемы «жадный» алгоритм даёт оптимальное решение, но так будет далеко не всегда. Например, для той же задачи с другой схемой (рис. 6.26) «жадный» алгоритм даст маршрут A-B-D-F длиной 10, хотя существует более короткий маршрут A-C-E-F длиной 7.
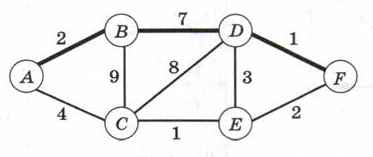
Рис. 6.26
«Жадный» алгоритм не всегда позволяет получить оптимальное решение.
Однако есть задачи, в которых «жадный» алгоритм всегда приводит к правильному решению. Одна из таких задач (её называют задачей Прима—Крускала в честь Р. Прима и Д. Крускала, которые независимо предложили её в середине XX века) формулируется так.
Следующая страница 
«Жадные» алгоритмы. Задача 2
Cкачать материалы урока
