Практическая работа № 3
«Сравнение алгоритмов сжатия»

При выполнении этой работы используются программы RLE (алгоритм сжатия RLE) и Huffman (кодирование Хаффмана и Шеннона-Фано).

1. Запустите программу Huffman.exe и закодируйте строку «ЕНОТ НЕ ТОНЕТ», используя методы Шеннона-Фано и Хаффмана. Запишите результаты в таблицу:

Сделайте выводы.

Ответ:

Как, по вашему мнению, будет изменяться коэффициент сжатия при увеличении длины текста, при условии, что набор символов и частота их встречаемости останутся неизменной? Проверьте ваш вывод с помощью программы (например, можно несколько раз скопировать ту же фразу).

Ответ:

2. Используя кнопку Анализ файла в программе Huffman, определите предельный теоретический коэффициент сжатия для файла a.txt при побайтном кодировании.

Ответ:

3. С помощью программ RLE и Huffman выполните сжатие файла a.txt разными способами. Запишите результаты в таблицу:

4. Используя кнопку Анализ файла в программе Huffman, определите предельный теоретический коэффициент сжатия для файла a.txt.huf при побайтном кодировании. Объясните результат.

Ответ:

5. Примените несколько раз повторное сжатие этого файла с помощью алгоритма Хаффмана (новые файлы получат имена a.txt.huf2, a.txt.huf3 и т.д.) и заполните таблицу, каждый раз выполняя анализ полученного файла.

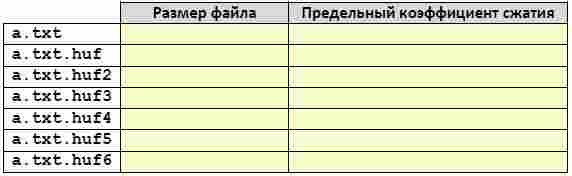
Объясните, почему с некоторого момента при повторном сжатии файла его размер увеличивается.

Ответ:

6. Выполните те же действия, используя метод Шеннона-Фано.

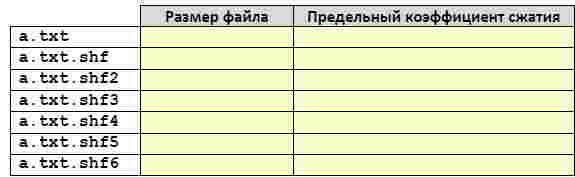
Объясните, почему с некоторого момента при повторном сжатии файла его размер увеличивается.

Ответ:

7. Сравните результаты сжатия этого файла с помощью алгоритма RLE, лучшие результаты, полученные методами Шеннона-Фано и Хаффмана, а также результат сжатия этого файла каким-нибудь архиватором.

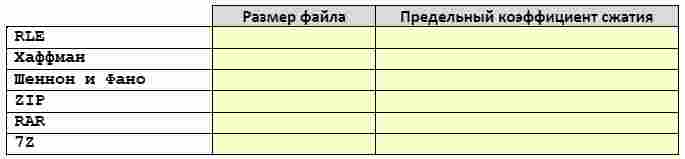
Объясните результаты и сделайте выводы.

Ответ: