Уроки 41 - 43
Моделирование зависимостей между величинами (§17)
Практическая работа 3.1. "Получение регрессионных моделей"
Содержание урока
Моделирование зависимостей между величинами (§17)
Величины и зависимости между ними
Математические модели
Практическая работа №3.1 Получение регрессионных моделей
Моделирование зависимостей между величинами (§17)
Математические модели
Если зависимость между величинами удается представить в математической форме, то мы имеем математическую модель.
Математическая модель — это совокупность количественных характеристик некоторого объекта (процесса) и связей между ними, представленных на языке математики.
Хорошо известны математические модели для первых двух примеров. Они отражают физические законы и представляются в виде формул:
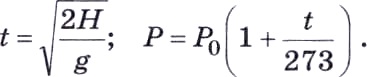
Это примеры зависимостей, представленных в функциональной форме. Первую зависимость называют корневой (время пропорционально квадратному корню высоты), вторую — линейной.
В более сложных задачах математические модели представляются в виде уравнений или систем уравнений. В конце данной главы будет рассмотрен пример математической модели, которая выражается системой неравенств.
В еще более сложных задачах (пример 3 — одна из них) зависимости тоже можно представить в математической форме, но не функциональной, а иной.
Табличные и графические модели
Рассмотрим примеры двух других, не формульных, способов представления зависимостей между величинами: табличного и графического. Представьте себе, что мы решили проверить закон свободного падения тела экспериментальным путем. Эксперимент организуем следующим образом: будем бросать стальной шарик с 6-метровой высоты, 9-метровой и т. д. (через 3 метра), замеряя высоту начального положения шарика и время падения. По результатам эксперимента составим таблицу и нарисуем график (рис. 3.2).
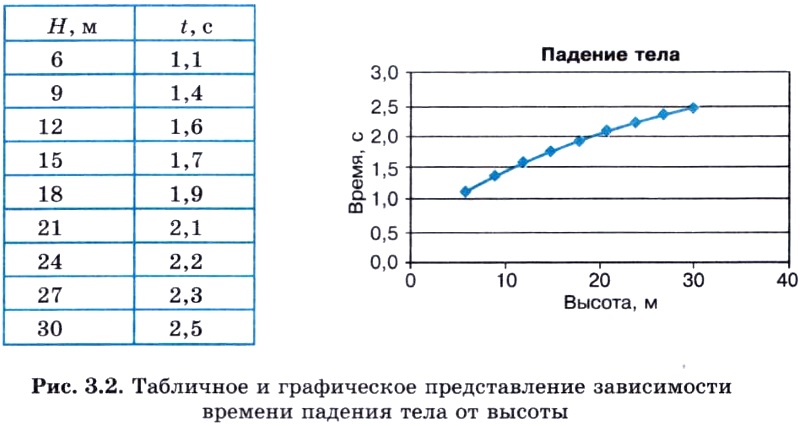
Если каждую пару значений Н и t из данной таблицы подставить в приведенную выше формулу зависимости времени от высоты, то формула превратится в равенство (с точностью до погрешности измерений). Значит, модель работает хорошо. (Однако если сбрасывать не стальной шарик, а большой легкий мяч, то равенство не будет достигаться, а если надувной шарик, то значения левой и правой частей формулы будут различаться очень сильно. Как вы думаете почему?)
В этом примере мы рассмотрели три способа моделирования зависимости величин: функциональный (формула), табличный и графический. Однако математической моделью процесса падения тела на землю можно назвать только формулу. Формула более универсальна, она позволяет определить время падения тела с любой высоты, а не только для того экспериментального набора значений Н, который отображен на рис. 3.2. Имея формулу, можно легко создать таблицу и построить график, а наоборот — весьма проблематично.
Точно так же тремя способами можно отобразить зависимость давления от температуры. Оба примера связаны с известными физическими законами — законами природы. Знания физических законов позволяют производить точные расчеты, они лежат в основе современной техники.
Информационные модели, которые описывают развитие систем во времени, имеют специальное название: динамические модели. В примере 1 приведена именно такая модель. В физике динамические информационные модели описывают движение тел, в биологии — развитие организмов или популяций животных, в химии — протекание химических реакций и т. д.
Следующая страница 
Вопросы и задания
