Контрольные тренировочные задания
(решения)
Часть 1
Задание 23
Решение примера 1
Сколько существует различных наборов значений логических переменных x1, x2, … x9, y1, y2, … y9, которые удовлетворяют всем перечисленным ниже условиям?
(¬ (x1 ≡ y1)) ≡ (x2 ≡ y2)
(¬ (x2 ≡ y2)) ≡ (x3 ≡ y3)
…
(¬ (x8 ≡ y8)) ≡ (x9 ≡ y9)
В ответе не нужно перечислять все различные наборы значений переменных x1, x2, … x9, y1, y2, … y9, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
Ответ: ___________________________.
Решение.
1) Для начала, найдем количество решений для первого уравнения. Из уравнения видно, что если две соседних переменные не равны, то следующая пара переменных обязательно должна быть равной:
(xi ≠ yi)→(xi+1 = yi+1).
Если первая пара переменных одинаковая, то следующая должна иметь разные значения: (xi = yi)→(xi+1 ≠ yi+1).
Исходя из этого правила, построим таблицу истинности для первого уравнения с нужными нам строками (при которых функция истинна).
Таблица 1
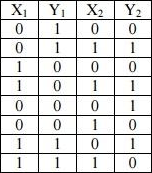
Пусть x1 и y1 имеют разные значения (0,1 или 1,0), тогда x2 и y2 будут одинаковы (0,0 или 1,1).
Пусть x1 и y1 имеют одинаковые значения (0,0 или 1,1), тогда x2 и y2 будут разные (0,1 или 1,0).
Вывод, по первому уравнению мы имеем 8 наборов переменных.
2) Теперь найдем количество решений для второго уравнения.
Варианты решений второго уравнения будут точно такими же, как и для первого.
Таблица 2
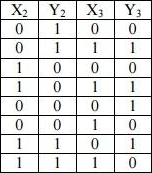
3) Добавим для второй таблицы два столбца для общих переменных: x1 и y1
Таблица 3
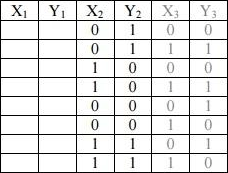
Не обращая внимания на столбцы значений x3 и y3 вставьте значения для x1 и y1, исходя из Таблицы 1.
Берем первую строку таблицы: x2=0, y2=1
Смотрим в Таблице 1, чему будут равны переменные x1 и y1 : при x2=0, а y2=1.
Значения переменных x1 и y1 могут быть либо x1=0, y1=0, либо x1=1, y1=1.
Если x2=1, а y3=0, то x1 и y1 также могут быть либо x1=0, y1=0, либо x1=1, y1=1.
Заполним всю таблицу:
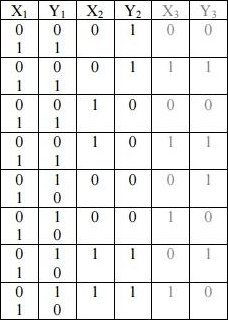
Из таблицы видно, что, после добавления второго уравнения, количество найденных решений увеличилось в два раза.
Все уравнения в нашей системе однотипны, значит каждое следующее уравнение также будет увеличивать количество решений в два раза.
Всего в данной системе 8 уравнений.
Следовательно: 8*2*2*2*2*2*2*2=1024 решения.
Ответ: 1024
Возврат на страницу Решение примеров части 1 задание 23


