Контрольные тренировочные задания
(решения)
Часть 1
Задание 23
Решение примера 2
Сколько существует различных наборов значений логических переменных x1, x2, … x6, y1, y2, … y6, которые удовлетворяют всем перечисленным ниже условиям?
(x1 → (x2/\ y1)) /\ (y1 → y2) = 1
(x2 → (x3/\ y2)) /\ (y2 → y3) = 1
…
(x5 → (x6/\ y5)) /\ (y5 → y6) = 1
x6 → y6 = 1
В ответе не нужно перечислять все различные наборы значений переменных x1, x2, … x6, y1, y2, … y6,, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
Ответ: ___________________________.
Решение.
В данной системе уравнений первые 5 уравнений однотипны и будут принимать значение 1 только в том случае, если каждый из множителей равен 1.
Например:
x1 → (x2/\ y1) = 1 и y1 → y2 = 1
Следовательно, для того чтобы все система уравнений была истинна необходимо, чтобы:
(y1 → y2) = 1
(y2 → y3) = 1
…
(y5 → y6) = 1
или
(y1 → y2) ∧ (y2 → y3) ∧ (y3 → y4) ∧ (y4 → y5) ∧ (y5 → y6) = 1
Чтобы данное уравнение было равно 1, необходимо и достаточно, чтобы yi ≤ yi+1.
Все наборы переменных y, которые удовлетворяют данному условию представим в виде таблицы:
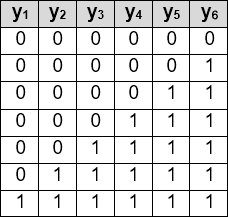
Чтобы вся система оставалась истинной необходимо, чтобы:
x1 → (x2/\ y1) = 1
x2 → (x3/\ y2) = 1
…
x5 → (x6/\ y5) = 1
Проанализируем правую часть этих уравнений:
Как только переменная xi примет значение 1, все последующие x должны быть равны 1, а также все y, начиная с yi должны быть равны 1.
Вывод:
— если x6 = 0, то нам подходят все 7 наборов y
— если x6 = 1, то нам подходят только 6 наборов y (выбираем те строки в таблице истинности, где y6=1)
— если x5 = 1, то нам подходят только 5 наборов y (выбираем те строки в таблице истинности, где y5=1)
— если x4 = 1, то нам подходят только 4 набора y (выбираем те строки в таблице истинности, где y4=1)
— если x3 = 1, то нам подходят только 3 набора y (выбираем те строки в таблице истинности, где y3=1)
— если x2 = 1, то нам подходят только 2 набора y (выбираем те строки в таблице истинности, где y2=1)
— если x1 = 1, то нам подходят только 1 набор y (выбираем те строки в таблице истинности, где y1=1)
Итого: 7+6+5+4+3+2+1=28
Ответ: 28
Возврат на страницу Решение примеров части 1 задание 23


