Контрольные тренировочные задания
(решения)

Часть 2

Задание 26

Решение примера 2

Два игрока, Паша и Валя, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Паша. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 20. Если при этом в куче оказалось не более 30 камней, то победителем считается игрок, сделавший последний ход. В противном случае победителем становится его противник. Например, если в куче было 17 камней и Паша удвоит количество камней в куче, то игра закончится, и победителем будет Валя. В начальный момент в куче было S камней, 1 ≤ S ≤ 19.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.

Выполните следующие задания.
1. а) При каких значениях числа S Паша может выиграть в один ход?
Укажите все такие значения и соответствующие ходы Паши.
б) У кого из игроков есть выигрышная стратегия при S = 18, 17, 16?
Опишите выигрышные стратегии для этих случаев.
2. У кого из игроков есть выигрышная стратегия при S = 9, 8? Опишите соответствующие выигрышные стратегии.
3. У кого из игроков есть выигрышная стратегия при S = 7? Постройте дерево всех партий, возможных при этой выигрышной стратегии (в виде рисунка или таблицы). На рёбрах дерева указывайте, кто делает ход; в узлах – количество камней в позиции.

Решение.

1. а) Паша может выиграть, если S = 19 или S = 10, 11, 12, 13, 14, 15. При S = 19 первым ходом нужно добавить в кучу один камень, при остальных указанных значениях S нужно удвоить количество камней.

б) При S = 16, 17 или 18 удваивать количество камней не имеет смысла, так как после такого хода выигрывает противник. Поэтому можно считать, что единственный возможный ход – это добавление в кучу одного камня.

При S = 18 после такого хода Паши в куче станет 19 камней. В этой позиции ходящий (т.е. Валя) выигрывает (смотрите пункт 1а): при S = 18 Паша (игрок, который должен ходить первым) проигрывает.

Выигрышная стратегия есть у Вали.

При S = 17, после того как Паша своим первым ходом добавит один камень, в куче станет 18 камней. В этой позиции ходящий (т.е. Валя) проигрывает (смотрите выше): при S = 17 Паша (игрок, который должен ходить первым) выигрывает. Выигрышная стратегия есть у Паши.

При S = 16 выигрышная стратегия есть у Вали. Действительно, если Паша первым ходом удваивает количество камней, то в куче становится 32 камня, и игра сразу заканчивается выигрышем Вали. Если Паша добавляет один камень, то в куче становится 17 камней. Как мы уже знаем, в этой позиции игрок, который должен ходить (т.е. Валя), выигрывает.

Во всех случаях выигрыш достигается тем, что при своём ходе игрок, имеющий выигрышную стратегию, должен добавить в кучу один камень.

Можно нарисовать деревья всех возможных партий для указанных значений S.
Другая возможность – (1) указать на то, что удваивать кучу не имеет смысла, и (2) последовательно сводить случай S = 18 к случаю S = 19, случай S = 17 – к случаю S = 18 и т.д.

2. При S = 9 или 8 выигрышная стратегия есть у Паши. Она состоит в том, чтобы удвоить количество камней в куче и получить кучу, в которой будет соответственно 18 или 16 камней. В обоих случаях игрок, который будет делать ход (теперь это Валя), проигрывает (смотрите пункт 1б).

3. При S = 7 выигрышная стратегия есть у Вали. После первого хода Паши в куче может стать либо 8, либо 14 камней. В обеих этих позициях выигрывает игрок, который будет делать ход (теперь это Валя). Случай S = 8 рассмотрен в пункте 2, случай S = 14 рассмотрен в пункте 1а.

В таблице изображено дерево возможных партий при описанной стратегии Вали. Заключительные позиции (в них выигрывает Валя) подчёркнуты. На рисунке это же дерево изображено в графическом виде (оба способа изображения дерева допустимы).

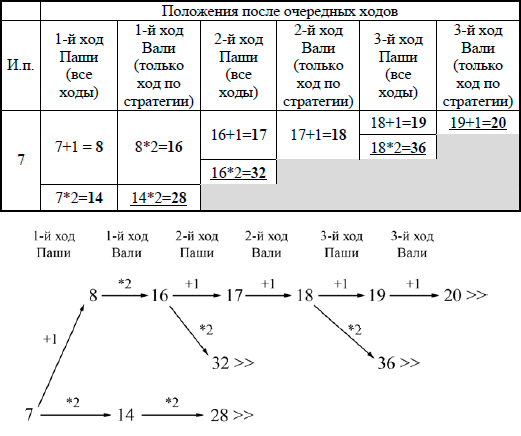
Дерево всех партий, возможных при Валиной стратегии. Знаком >> обозначены позиции, в которых партия заканчивается.

Возврат на страницу    Решение примеров части 2 задание 26