Урок 7
Дискретная форма представления информации
Содержание урока
1.5.1. Преобразование информации из непрерывной формы в дискретную
1.5.2. Двоичное кодирование
1.5.3. Универсальность двоичного кодирования. 1.5.4. Равномерные и неравномерные коды
Электронное приложение к учебнику
Единая коллекция цифровых образовательных ресурсов
1.5.2. Двоичное кодирование
В общем случае, чтобы представить информацию в дискретной форме, её следует выразить с помощью символов какого-нибудь естественного или формального языка. Таких языков тысячи. Каждый язык имеет свой алфавит.
Алфавит — конечный набор отличных друг от друга символов (знаков), используемых для представления информации. Мощность алфавита — это количество входящих в него символов (знаков).
Алфавит, содержащий два символа, называется двоичным алфавитом (рис. 1.11). Представление информации с помощью двоичного алфавита называют двоичным кодированием. Закодировав таким способом информацию, мы получим её двоичный код.
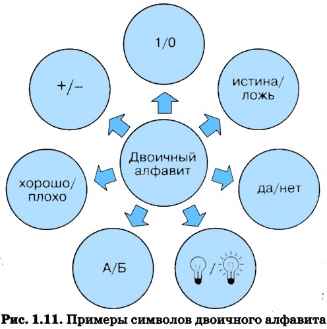
Рассмотрим в качестве символов двоичного алфавита цифры 0 и 1.
Покажем, что любой алфавит можно заменить двоичным алфавитом. Прежде всего, присвоим каждому символу рассматриваемого алфавита порядковый номер. Номер представим с помощью двоичного алфавита. Полученный двоичный код будем считать кодом исходного символа (рис. 1.12).
Если мощность исходного алфавита больше двух, то для кодирования символа этого алфавита потребуется не один, а несколько двоичных символов. Другими словами, порядковому номеру каждого символа исходного алфавита будет поставлена в соответствие цепочка (последовательность) из нескольких двоичных символов.
Правило получения двоичных кодов для символов алфавита мощностью больше двух можно представить схемой на рис. 1.13.
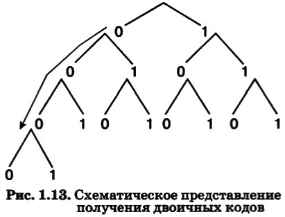
Двоичные символы (0,1) здесь берутся в заданном алфавитном порядке и размещаются слева направо. Двоичные коды (цепочки символов) читаются сверху вниз. Все цепочки (кодовые комбинации) из двух двоичных символов позволяют представить четыре различных символа произвольного алфавита:
Цепочки из трёх двоичных символов получаются дополнением двухразрядных двоичных кодов справа символом 0 или 1. В итоге кодовых комбинаций из трёх двоичных символов получается 8 — вдвое больше, чем из двух двоичных символов:
Соответственно, четырёхразрядный двоичный код позволяет получить 16 кодовых комбинаций, пятиразрядный — 32, шестиразрядный — 64 и т. д.
Длину двоичной цепочки — количество символов в двоичном коде — называют разрядностью двоичного кода.
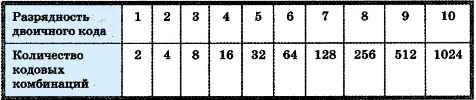
Обратите внимание, что:
4 = 2-2, 8=2 2-2, 16 = 2 2 2 2, 32 = 2-2-2-2-2 и т. д.
Здесь количество кодовых комбинаций представляет собой произведение некоторого количества одинаковых множителей, равного разрядности двоичного кода.
Если количество кодовых комбинаций обозначить буквой N, а разрядность двоичного кода — буквой i, то выявленная закономерность в обшем виде будет записана так:
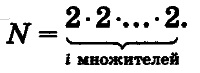
В математике такие произведения записывают в виде:
N = 2 i.
Запись 2i читают так: «2 в i-й степени».
Зядача. Вождь племени Мульти поручил своему министру разработать двоичный код и перевести в него всю важную информацию. Двоичный код какой разрядности потребуется, если алфавит, используемый племенем Мульти, содержит 16 символов? Выпишите все кодовые комбинации.
Решение. Так как алфавит племени Мульти состоит из 16 символов, то и кодовых комбинаций им нужно 16. В этом случае длина (разрядность) двоичного кода определяется из соотношения: 16 = 2 i. Отсюда i = 4.
Чтобы выписать все кодовые комбинации из четырёх 0 и 1, воспользуемся схемой на рис. 1.13: 0000, 0001, 0010, ООН, 0100, 0101, 0110, 0111,1000,1001,1010,1011,11Q0,1101,1110,1111.
На сайте http://sc.edu.ru/ размещена виртуальная лаборатория «Цифровые весы» (135009). С её помощью вы можете самостоятельно открыть метод разностей — ещё один способ получения двоичного кода целых десятичных чисел.
