Урок 4
§7. Системы счисления
Содержание урока
Что такое система счисления?
Непозиционные системы счисления
Позиционные системы счисления
Выводы. Интеллект-карта
Вопросы и задания
Проект
Позиционные системы счисления
Позиционная система счисления — это такая система, в которой значение цифры полностью определяется её местом (позицией) в записи числа.
Пример позиционной системы счисления — привычная нам десятичная система. В числе 6375 цифра 6 обозначает тысячи (6000), цифра 3 — сотни (300), цифра 7 — десятки (70), а цифра 5 — единицы:
6375 = 6 • 1000 + 3 • 100 + 7 • 10 + 5 • 1
Алфавит системы счисления — это используемый в ней набор цифр.
Основание системы счисления — это количество цифр в алфавите (мощность алфавита).
В десятичной системе основание — 10, алфавит состоит из 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Число 10, вероятно, было выбрано потому, что люди сначала использовали для счета свои 10 пальцев на руках.
Разряд — это позиция цифры в записи числа. Разряды в записи целых чисел нумеруются с нуля справа налево.
В числе 6375 цифра 6 стоит в третьем разряде (тысячи, 103), 3 — во втором разряде (сотни, 102), 7 — в первом (десятки, 101), а 5 — в нулевом (единицы, 100). Поэтому
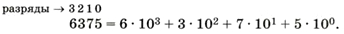
Это развёрнутая форма записи числа. Не забывайте, что любое число (кроме нуля!) в нулевой степени равно 1.
Запишите числа 158 и 1879 в развёрнутой форме.
Используя развёрнутую форму записи числа в десятичной системе счисления, определите, чему равен:
а) остаток от деления некоторого числа на 10;
б) остаток от деления некоторого числа на 100.
Как определить, что число без остатка делится на 10? На 100?
Все другие позиционные системы счисления, которые мы будем изучать, устроены так же, как и десятичная система, изменяется только основание. В первую очередь нас будет интересовать двоичная система (система с основанием 2). Она позволяет записать любое число в двоичном коде, который используется в компьютерах для хранения всех данных.
Мы познакомимся также с восьмеричной и шестнадцатеричной системами, которые применяют для сжатой записи двоичных кодов.
Как вы думаете, какие основания имеют восьмеричная и шестнадцатеричная системы счисления?
Какой алфавит может быть у двоичной системы счисления? У восьмеричной системы? У шестнадцатеричной системы?
Если число записано в позиционной системе с основанием, не равным 10, это основание записывают справа от числа как нижний индекс. Например, число 101102 записано в двоичной системе, 1235 — в пятеричной, а 7458 — в восьмеричной, а 29616 — в шестнадцатеричной.
Запишите числа 101102, 1235 , 7458 и 29616 в развёрнутой форме и представьте их в десятичной системе счисления.
Найдите числа, которые записаны неправильно.
4568 1022 36512 5788 1729 5214
Как вы рассуждали?
Представьте число 23 в развёрнутой форме через степени числа 2. Как теперь можно записать это число в двоичной системе счисления?
Составьте таблицу степеней числа 2, от 21 до 213.
Для чисел 12, 75, 150 и 513 определите старшую степень числа в развёрнутой форме через степени числа 2. Как вы рассуждали?
Сформулируйте правило перевода числа из любой позиционной системы в десятичную.
Если основание системы счисления неизвестно, всё равно можно записать число в развёрнутой форме, обозначив основание как неизвестную величину х:
325х = 3 • х2 + 2 • х1 + 5 • х0 = 3 - х2 + 2 • х + 5.
В последнем равенстве учтено, что х1 = х и х0 = 1.
Задача. В некоторой системе счисления число 58 записывается как 46x. Определите основание х этой системы счисления.
Решение. Поскольку в записи числа 46x. есть цифра 6, можно сразу сказать, что х > 6 (в алфавитах систем счисления с меньшим основанием цифры 6 нет). Представим число 46x в развёрнутой форме: 46x = 4 • х + 6, и приравняем к 58:
4 • х + 6 = 58.
Решив это уравнение, получаем: х = 13.
В некоторой системе счисления число 45 записывается как 63x. Определите основание х этой системы счисления.
Найдите основание х системы счисления, в которой выполняется равенство 16x + 33x = 52x.
Найдите все основания х систем счисления, в которых верно неравенство 2x + 32x > 102x .
Как записывается наименьшее трёхзначное число в системе счисления с основанием х? Чему оно равно в десятичной системе?
Как записывается наибольшее трёхзначное число в системе счисления с основанием х? Чему оно равно в десятичной системе?
Найдите наименьшее основание системы счисления, в которой запись числа 30 имеет 3 значащих разряда.
Вася составил задачу: «В какой системе счисления число 15 записывается как 25x?». Есть ли у неё решение? Обоснуйте ответ.
Следующая страница 
Выводы. Интеллект-карта
Cкачать материалы урока
