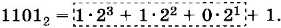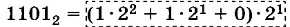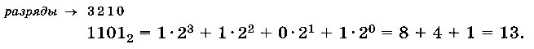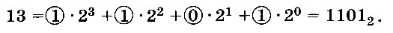Уроки 12 - 13
§8. Двоичная система счисления
Содержание урока
Перевод чисел
Арифметические действия
Недостатки двоичной системы счисления
Выводы. Интеллект-карта
Вопросы и задания
Перевод чисел
Ключевые слова:
• двоичная система
• перевод чисел
• сложение
• вычитание
• перенос
• заём
В двоичной системе основание — 2, а алфавит состоит из двух цифр 0 и 1. Двоичная система счисления — самая важная для компьютеров, потому что все данные хранятся, обрабатываются и передаются именно в двоичном коде, как цепочки нулей и единиц. Двоичная система обладает важными достоинствами:
• для того чтобы построить компьютер, работающий с двоичными данными, достаточно иметь устройства с двумя состояниями (включено/выключено); оказалось, что сделать такие электронные устройства проще, чем какие-то другие, в том числе десятичные;
• действия над двоичными числами выполняются по очень простым правилам, поэтому все устройства компьютера тоже получаются достаточно простыми.
Перевод чисел
В предыдущем параграфе, решая задачи, вы научились переводить числа из любой позиционной системы в десятичную и обратно. Теперь применим эти знания для работы с двоичными числами.
Предположим, что нам дано двоичное число 11012. Нижний индекс «2» в этой записи обозначает основание системы счисления. Определим, какое это число (как оно записывается в десятичной системе). Запишем его в развёрнутой форме, так же как мы делали в предыдущем параграфе, но учтём, что основание здесь равно 2:
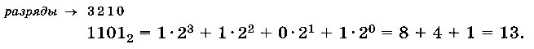
Так с помощью развёрнутой формы записи числа мы перевели его в десятичную систему.
Переведите в десятичную систему счисления числа 10112 , 10012 , 11112 .
Василий перевёл некоторое число в двоичную систему счисления, эта запись содержит 5 цифр. Какое это могло быть число (назовите наименьшее и наибольшее возможные значения)?
Теперь осталось научиться решать обратную задачу: переводить числа из десятичной системы в двоичную. Это значит, что нужно получить 11012 из 13.
Заметим, что для этого нам достаточно записать число как сумму степеней основания числа 2, т. е. в развёрнутой форме. Полученные коэффициенты при степенях двойки будут цифрами двоичной записи числа.
Покажем, как работает этот способ для числа 13. Выделим из 13 старшую степень двойки — это 8 = 23 (потому что 24 = 16 будет уже больше 13):
13 = 8 + 5 = 23 +5.
Дальше из «остатка» 5 снова выделяем старшую степень двойки — это 4 = 22:
13 = 23 + 4 + 1 = 23 + 22 + 1.
Оставшаяся единица — это тоже степень двойки: 20 = 1, поэтому получаем:
13 = 23 + 22 + 20.
Здесь не хватает ещё одного разряда, 21, можно добавить его к сумме, умножив на 0:
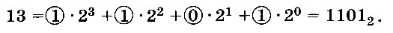
Таким образом, мы фактически получили развёрнутую запись числа 13 в двоичной системе счисления. Числа, обведённые кружками, — это цифры записи числа в двоичной системе счисления. Поэтому 13 = 11012.
Переведите в двоичную систему счисления все натуральные числа от 1 до 16.
Переведите в двоичную систему счисления числа 19, 25, 31, 56.
Существует и другой, «более математический» способ. Запишем число в развёрнутой форме:
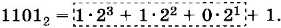
На какое число делится нацело сумма, обведённая рамкой? Какая часть полной суммы не делится на это число? Как она называется?
С помощью какой математической операции можно найти последнюю цифру двоичной записи числа?
Вынесем за скобку 2 (основание системы счисления):
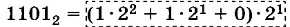
Какое число записано в скобках в развёрнутой форме? Как связано это число с исходным числом 11012?
Какие числа получатся, если эти числа разделить на 2 и отбросить остаток?
11102 10112 110112 100012
Запишите результаты в двоичной системе счисления.
Для перевода числа из десятичной системы в систему счисления с основанием 2 нужно делить это число на 2, отбрасывая остаток на каждом шаге, пока не получится 0. Затем выписать найденные остатки в обратном порядке.
Переведём в двоичную систему число 19 с помощью этого алгоритма. В результате многократного деления на 2 (пока на очередном шаге в частном не получится 0) находим
19 = 100112 (рис. 2.14).

Рис. 2.14
Вспомним, что остатки — это цифры двоичной записи числа, начиная с последней. Поэтому их нужно выписать в обратном порядке (по стрелкам на рис. 2.14):
19 = 100112.
Как по двоичной записи числа определить, чётное оно или нет?
Переведите в двоичную систему счисления числа 16, 20, 24, 28. Как по двоичной записи числа сразу определить, делится ли оно на 4? На 8? На 16?
Следующая страница  Арифметические действия
Арифметические действия
Cкачать материалы урока